Derivative as a concept | Derivatives introduction | AP Calculus AB | Khan Academy
TLDRThe video tutorial delves into the fundamental concept of the slope of a line, illustrating it as the rate of change of one variable with respect to another, typically represented as 'rise over run'. Transitioning from basic algebra to calculus, the instructor introduces the notion of the derivative, or the instantaneous rate of change, which unlike the constant slope of a straight line, varies along a curve. Using vivid examples and clear explanations, the concept of the derivative is linked to real-world phenomena, like calculating the speed of a sprinter at a precise moment. The video further explores Leibniz's notation for derivatives, demonstrating the transition from average rates to instantaneous rates as we consider infinitesimally small intervals.
Takeaways
- 📉 The slope of a line represents the rate of change of a vertical variable with respect to a horizontal variable, typically described as 'rise over run'.
- 🔍 To calculate the slope, you select two points on the line, determine the change in x (horizontal) and y (vertical), and divide the change in y by the change in x.
- 📚 The concept of slope is fundamental and a precursor to understanding more complex calculus concepts, such as derivatives and instantaneous rates of change.
- 🌐 Calculus extends the idea of a slope from straight lines to curves, where the rate of change can vary at every point.
- 📈 A tangent line to a curve at a given point represents the instantaneous rate of change at that point, which is the essence of differential calculus.
- 💡 The derivative is the slope of the tangent line at a point on the curve, symbolizing the instantaneous rate of change.
- ✍️ Leibniz's notation (dy/dx) for derivatives emphasizes tiny changes in y for tiny changes in x, approaching zero, reflecting super small intervals of change.
- 🔢 The derivative of a function at a point can be represented using different notations, including 'f prime of x' (Lagrange notation) and 'y dot' (common in physics).
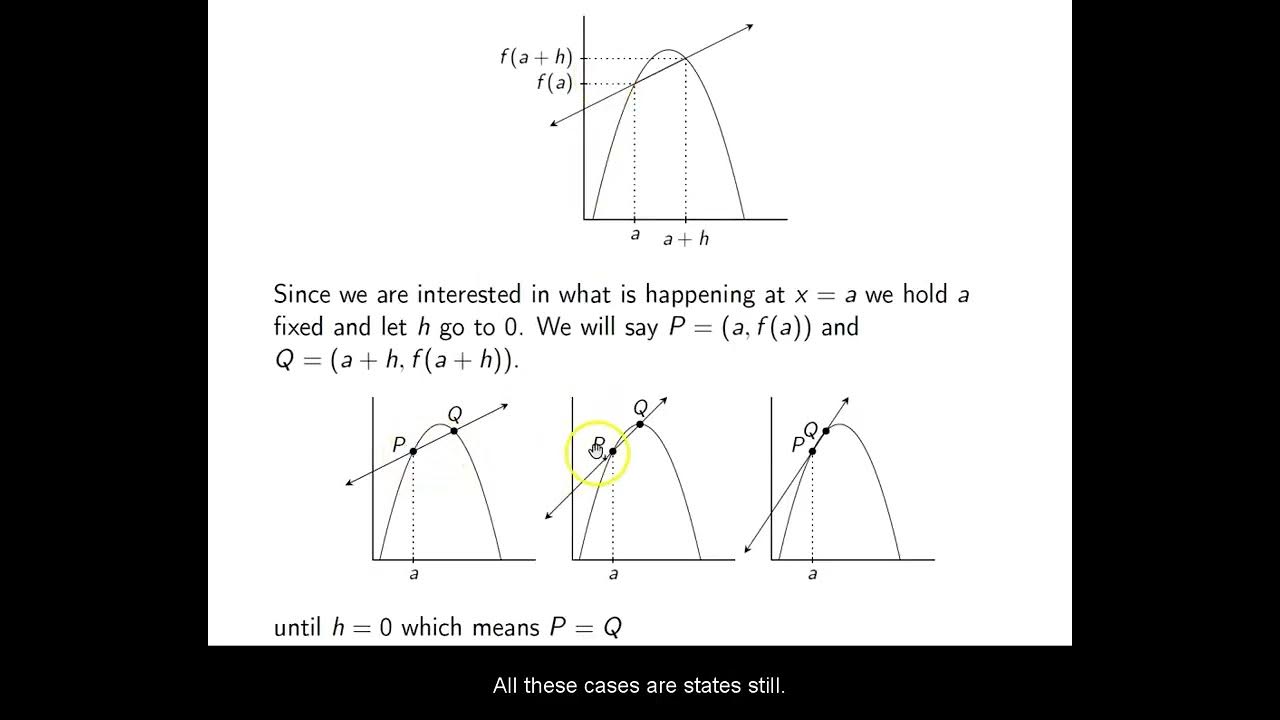
- 🤔 Understanding derivatives involves getting progressively closer between two points on a curve and examining the limit as the interval approaches zero.
- 🎓 Calculus tools enable us to derive general equations for derivatives that apply to any point on a curve, offering a broad utility in mathematical and scientific analyses.
Q & A
What is the concept of slope in the context of a line?
-The slope of a line describes the rate of change of a vertical variable with respect to a horizontal variable. It is calculated by determining the change in y (vertical change) over the change in x (horizontal change) between two points on the line.
What is the significance of the slope being constant for any two points on a line?
-A constant slope indicates that the line has a uniform rate of change, which is a defining characteristic of a linear function. No matter how far apart or close together the two points are on the line, the calculated slope remains the same.
How does calculus extend the concept of slope to curves?
-Calculus introduces the concept of the instantaneous rate of change, which allows us to consider the rate of change at a specific point on a curve, even when the rate of change is not constant. This is done by finding the slope of the tangent line at that point.
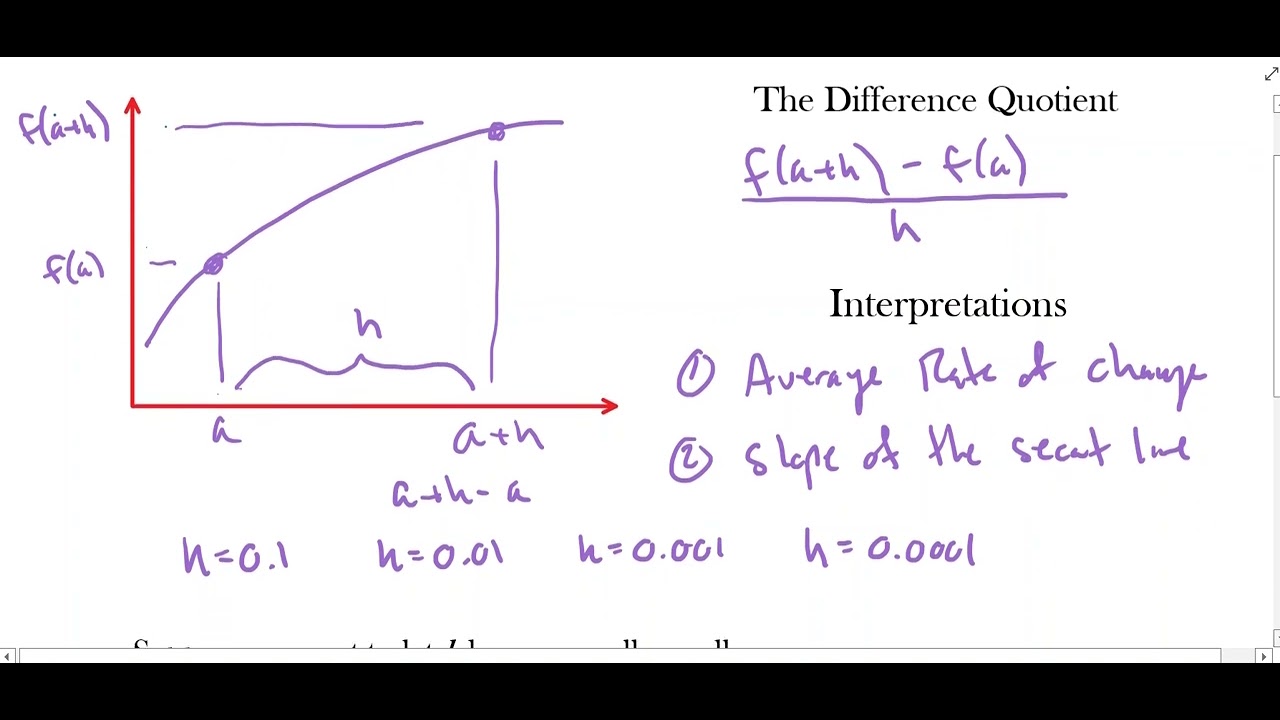
What is the average rate of change between two points on a curve?
-The average rate of change between two points on a curve is the slope of the secant line that connects those points. It represents the change in y divided by the change in x over the interval between the two points.
How does the instantaneous rate of change differ from the average rate of change?
-The instantaneous rate of change is the rate of change at a specific point, found by taking the limit as the interval between two points approaches zero, effectively finding the slope of the tangent line at that point. In contrast, the average rate of change is calculated over an interval between two points and can vary depending on the interval chosen.
What is the derivative in the context of calculus?
-The derivative in calculus is the slope of the tangent line to a curve at a given point, which represents the instantaneous rate of change of the function at that point. It is a fundamental concept in differential calculus.
Who are the two individuals credited with the development of calculus?
-Isaac Newton and Gottfried Wilhelm Leibniz are credited with the development of calculus. Leibniz's notation for derivatives, using 'dy/dx', is particularly noteworthy.
What does Leibniz's notation 'dy/dx' represent?
-Leibniz's notation 'dy/dx' represents the derivative of y with respect to x, or the rate of change of y for an infinitesimally small change in x. It is a way to express the slope of the tangent line to a curve at a point as x approaches that point.
What is another notation used to denote the derivative of a function?
-Another notation for the derivative is 'f' prime, written as 'f' with a tick mark above it (f') or as 'f prime of x' (f'(x)), which indicates the slope of the tangent line to the curve y = f(x) at a specific point x.
How does the notation 'y with a dot over it' relate to the concept of derivatives?
-The notation 'y with a dot over it' (ẏ) is often used in physics to denote the derivative of y with respect to time, representing the instantaneous rate of change of y at a particular moment.
What role do limits play in calculating derivatives?
-Limits are crucial in calculating derivatives as they allow us to find the derivative by taking the limit of the average rate of change as the interval between two points approaches zero. This process defines the derivative as the instantaneous rate of change at a point.
How will the study of calculus help in understanding general equations for derivatives?
-The study of calculus provides the tools and techniques to derive general equations for derivatives, allowing us to find the instantaneous rate of change for any given point on a curve, not just at specific points, but for the entire function.
Outlines
🔢 Introduction to Slope and Its Relevance in Calculus
The instructor begins by reinforcing the concept of slope as a rate of change between two variables, illustrated with the traditional x and y axes. The video explains how slope is calculated by picking two points on a line and dividing the change in y by the change in x, termed as 'rise over run'. It emphasizes that the consistency of slope across any two points is what defines a line. The discussion transitions into calculus, introducing the concept of the slope of curves, which unlike lines, have a changing rate of change. It culminates in explaining the importance of calculus in understanding the instantaneous rate of change at a point on a curve through the concept of derivatives and tangent lines.
📈 Deep Dive into Derivatives and Notations in Calculus
This paragraph delves deeper into calculus, focusing on how derivatives are calculated and different notations used to express them. It explains Leibniz's differential notation which represents very small changes in variables as they approach zero, and how this forms the basis for calculating derivatives. Additionally, the instructor mentions other notations like Lagrange's notation, represented by 'f prime', and the dot notation used in physics, which both describe the slope of tangent lines at specific points. The paragraph concludes by highlighting the importance of limits in calculus, as they allow for the precise calculation of the derivative at any given point, preparing the viewer for more advanced topics in calculus.
Mindmap
Keywords
💡Slope
💡Rate of Change
💡Derivative
💡Tangent Line
💡Secant Line
💡Leibniz's Notation
💡Instantaneous Rate of Change
💡Differential Notation
💡Function
💡Limit
Highlights
Introduction to the concept of slope as the rate of change between two variables.
Explanation of how to calculate slope using two points on a line.
The Greek letter delta introduced as a shorthand for 'change'.
Slope is described as the change in y over the change in x.
Demonstration of slope as a constant for straight lines, regardless of the points chosen.
Introduction to calculus as a means to explore rates of change not just in straight lines but in curves.
Discussion of the limitations of traditional tools in calculating the rate of change for curves.
The concept of the secant line as a tool to measure average rate of change over a curve.
Exploration of the idea of instantaneous rate of change at a specific point on a curve.
Introduction of the tangent line as a method to approximate instantaneous rate of change.
Explanation of the derivative as the slope of the tangent line at a given point.
Leibniz's notation introduced as a method to express derivatives.
Comparison between delta and differential notation to signify changes approaching zero.
Different notations for derivatives, including Leibniz's, Lagrange's, and Newton's.
Future application of limits to define derivatives, emphasizing the role of approaching zero.
Promise of deriving general equations to describe derivatives for any given point.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: