Ch. 12.1 Sequences and Summation Notation

Prof. Williams

6 May 202222:14

EducationalLearning

32 Likes 10 Comments

TLDRThis lecture introduces the concept of sequences and series, emphasizing their importance in calculus. It explains sequences as ordered lists of numbers following a pattern and series as the sum of these numbers. The instructor outlines different types of sequences, including natural numbers, even and odd integers, and squares, providing general and recursive definitions for each. The Fibonacci sequence is highlighted for its prevalence in nature and mathematics. The lecture also covers summation notation, partial sums, and properties of sums, offering examples to illustrate these concepts.

Takeaways

📚 The script introduces Chapter 12, focusing on sequences and series, which are sets of numbers that follow a pattern and are crucial in calculus.
🔢 A sequence is a list of numbers with a discernible pattern, and the general term or formula that describes it is of great interest, especially in calculus.
📈 Basic sequences are explored, including natural numbers (n), even numbers (2n), odd numbers (2n-1), and a shifted sequence of odd numbers (2n+1), each with its general term.
📊 The script explains how to plot sequences, emphasizing that they are graphed in order, which is important for understanding their behavior, especially in higher-level math classes.
🔄 Recursive definitions of sequences are discussed, where each term is defined based on its relationship to the previous term, differing from general terms.
🌐 The Fibonacci sequence is highlighted as a significant example, where each term is the sum of the two preceding ones, and its prevalence in nature and the golden ratio.
📏 The concept of nth partial sums is introduced, which is the sum of the first n terms of a sequence, and how it can form a new sequence itself.
📝 Summation notation, represented by the Greek letter sigma (Σ), is explained as a way to denote the addition of a series of terms, which is fundamental in advanced mathematics.
📉 The script provides an example of calculating a partial sum using summation notation, demonstrating how to substitute values into the formula to find the sum.
🔀 It is noted that the index of summation can be shifted without changing the sequence of values, showing the flexibility in representing the same sequence.
📚 The properties of sums are briefly mentioned, with emphasis on factoring out constants and separating sums with addition or subtraction within the general term.

Q & A

What is the main topic of Chapter 12 discussed in the script?
-The main topic of Chapter 12 is sequences and series, which are sets of numbers that follow a pattern and are important in calculus.
What is a sequence in the context of the script?
-A sequence is a list of numbers that follow a specific pattern, and the focus is on identifying that pattern and understanding what happens when all the numbers in the sequence are added together.
What is the general term in a sequence?
-The general term in a sequence is the formula that represents the nth term of the sequence, allowing us to find any term in the sequence by substituting the appropriate index value.
Can you provide an example of a simple sequence from the script?
-An example of a simple sequence from the script is the natural numbers: 1, 2, 3, 4, and so on, where the general term is just n.
How is the sequence of even positive integers represented in general form?
-The sequence of even positive integers is represented in general form as 2n, where n is the index of the term in the sequence.
What is the general term for the sequence of odd positive integers?
-The general term for the sequence of odd positive integers is 2n - 1.
How is the sequence 3, 5, 7, 9 described in general form?
-The sequence 3, 5, 7, 9 is described in general form as 2n + 1, which represents the odd numbers shifted by one.
What operation is used to generate the sequence 1, 4, 9, 16, ... in the script?
-The sequence 1, 4, 9, 16, ... is generated by squaring each term, which is represented by the general term n squared (n^2).
What is the concept of a recursive definition in sequences?
-A recursive definition in sequences describes the next term in the sequence based on its relationship to the previous term, often starting with an initial term and a rule for finding subsequent terms.
Can you explain the Fibonacci sequence as mentioned in the script?
-The Fibonacci sequence is a series of numbers where each term is the sum of the two preceding ones, usually starting with 1 and 1. It is a common sequence found in nature and has many applications, including the golden ratio.
What is the purpose of summation notation (sigma notation) in mathematics?
-Summation notation, or sigma notation, is used to represent the sum of a sequence of terms in a compact form, making it easier to express and manipulate series in mathematical expressions.
What is the nth partial sum in the context of sequences?
-The nth partial sum is the sum of the first n terms of a sequence, providing a way to analyze the cumulative effect of the sequence's terms up to a certain point.
How can the properties of sums be applied in mathematical expressions?
-The properties of sums allow for manipulations such as factoring out constants or separating sums into multiple sums, which can simplify calculations and reveal patterns within sequences and series.

Outlines

00:00

📚 Introduction to Sequences and Series

The script introduces the concept of sequences and series, highlighting their importance in calculus. A sequence is described as a list of numbers that follow a pattern, and the focus is on identifying the pattern and the sum of the numbers. The general term of a sequence is emphasized as a key element. Basic sequences such as natural numbers, even and odd integers, and squares are introduced with their general terms, illustrating how to derive these from simple operations.

05:02

📈 Graphing and Describing Sequences

This section discusses how to graph sequences by plotting numbers in order and how plotting can be used to observe if a sequence levels out, a concept that becomes significant in higher-level calculus classes. The script also introduces recursive definitions of sequences, explaining how to find subsequent terms based on the previous ones, and provides examples for the previously mentioned sequences, emphasizing the different starting points and recursive formulas.

10:02

🌱 The Fibonacci Sequence and Its Relevance

The Fibonacci sequence is explored as a series where each term is the sum of the two preceding ones, starting from 1. The script explains the prevalence of the Fibonacci sequence in nature, such as in tree branching patterns, flower petal arrangements, snail shells, and even galaxy spirals. It also touches on the concept of the nth partial sum, which is the sum of the first n terms of a sequence, and provides an example with the sequence of squares, leading to a well-known sequence formula.

15:04

🔢 Summation Notation and Properties

The script introduces summation notation, also known as sigma notation, which is used to represent the sum of a series of terms. It explains the components of the notation, including the index, starting and ending values, and the general form of the terms being summed. An example is given to demonstrate how to calculate the sum of a series using this notation. Additionally, the script briefly mentions the ability to shift the index in a summation and the properties of sums, such as factoring out constants and separating sums with addition or subtraction within the general term.

20:06

📘 Advanced Summation Concepts

While not delving deeply into advanced topics, the script makes the audience aware that summations can have multiple representations for the same sequence of numbers. It also briefly touches on the properties of sums, suggesting that interested students can explore these in more depth in calculus textbooks. The script concludes by emphasizing two important properties of sums: factoring out constants and separating sums with internal addition or subtraction.

Mindmap

Keywords

💡Sequence

A sequence is a list of numbers that follow a specific pattern. In the context of the video, sequences are foundational to understanding series in calculus. The script introduces various types of sequences, such as natural numbers, even integers, and odd integers, to illustrate different patterns. For instance, the natural numbers sequence is represented by the general term 'n', starting from 1 and incrementing by 1 for each subsequent term.

💡Summation

Summation refers to the process of adding numbers together, especially in the context of sequences and series. The video emphasizes the importance of summation in calculus, where it is used to find the total of all terms in a sequence. The script explains the concept through the use of summation notation, denoted by the Greek letter sigma (Σ), which is used to represent the sum of a series of terms from a starting index to an ending index.

💡General Term

The general term of a sequence is the formula that describes the nth term in the sequence. It is crucial for identifying the pattern of a sequence. The script mentions that understanding the general term is key to determining what happens when all the numbers in a sequence are added together, as it allows for the prediction of any term in the sequence without listing them all.

💡Natural Numbers

Natural numbers are the set of positive integers starting from 1 and increasing by one. In the script, natural numbers are introduced as the simplest form of a sequence with the general term 'n', where each term is simply the value of 'n' itself, illustrating the concept of a sequence in its most basic form.

💡Even Positive Integers

Even positive integers are numbers that are divisible by 2 and greater than zero. The script describes a sequence of even positive integers with the general term '2n', where each term is twice the value of the sequence's position in the list, such as 2, 4, 6, 8, etc.

💡Odd Numbers

Odd numbers are integers that are not divisible by 2. The video script introduces a sequence of positive odd numbers with the general term '2n - 1', which captures the pattern of odd numbers by starting with 1 and increasing by 2 for each subsequent term, such as 1, 3, 5, 7, etc.

💡Recursive Definition

A recursive definition describes the next term in a sequence based on the previous term(s). The script explains how sequences can be defined recursively, where each term is found by adding a certain value to the term before it. This is exemplified in the script with the counting numbers sequence, which is defined recursively as starting at 1 and each subsequent term being the previous term plus one.

💡Fibonacci Sequence

The Fibonacci sequence is a series of numbers where each term is the sum of the two preceding ones, usually starting with 0 and 1. The script highlights the Fibonacci sequence as a common and important sequence in mathematics, with applications in nature, art, and even the stock market. The sequence begins with 1, 1, 2, 3, 5, 8, and so on, where each term is found by adding the two previous terms.

💡Partial Sum

A partial sum is the sum of the first n terms of a sequence. The script discusses the concept of partial sums in relation to sequences, showing how they can be used to create a new sequence of sums. For example, if the sequence is defined by 'n squared', the partial sums would be the cumulative totals of the squares of the first n natural numbers.

💡Sigma Notation

Sigma notation, represented by the Greek letter Σ, is a mathematical notation used to represent the summation of a series. The script introduces sigma notation as a way to express the sum of a sequence's terms in a concise form, where the index of summation (k) starts at a certain value (c) and ends at a specified number (n), with each term being represented by a general form (a_k).

Highlights

Introduction to Chapter 12 on sequences and summation notation, emphasizing its importance in calculus.

Definition of a sequence as a set of numbers following a pattern and the significance of identifying the pattern.

Explanation of the general term in a sequence and its importance for understanding the sequence's behavior.

Illustration of basic sequences such as natural numbers, even positive integers, and positive odd integers with their general terms.

Introduction of the concept of graphing sequences to observe patterns or levels, with an example of plotting a sequence.

Description of recursive definitions of sequences, relating each term to the previous one.

Recursive examples for natural numbers, even integers, and odd integers, showing different starting points and rates of change.

Introduction of the Fibonacci sequence, a series where each term is the sum of the two preceding ones, and its prevalence in nature.

Examples of how the Fibonacci sequence appears in branching patterns of trees, flowering patterns, and spiral patterns in nature.

Graphical representation of the Fibonacci sequence using rectangles and squares with areas corresponding to the sequence.

Explanation of the nth partial sum as the sum of the first n terms of a sequence.

Demonstration of finding the sequence of partial sums for a sequence defined by n squared, and the resulting sequence pattern.

Introduction to summation notation, also known as sigma notation, used for expressing the sum of a sequence.

Description of summation notation components including the index, starting value, ending value, and general form of terms.

Example calculation using summation notation to find the sum of a series with a specific formula.

Discussion on the flexibility of summation notation to represent the same sequence with different starting indices.

Mention of properties of sums, such as factoring out constants and separating addition or subtraction within the general term.

Transcripts

Browse More Related Video

AP Calculus BC Lesson 10.1

Unit VII: Lec 1 | MIT Calculus Revisited: Single Variable Calculus

Explicit and recursive definitions of sequences | Precalculus | Khan Academy

Sequence and Series | Terms of Sequence and Associated Series | Pre-Calculus

Ch. 12.2 Arithmetic Sequences

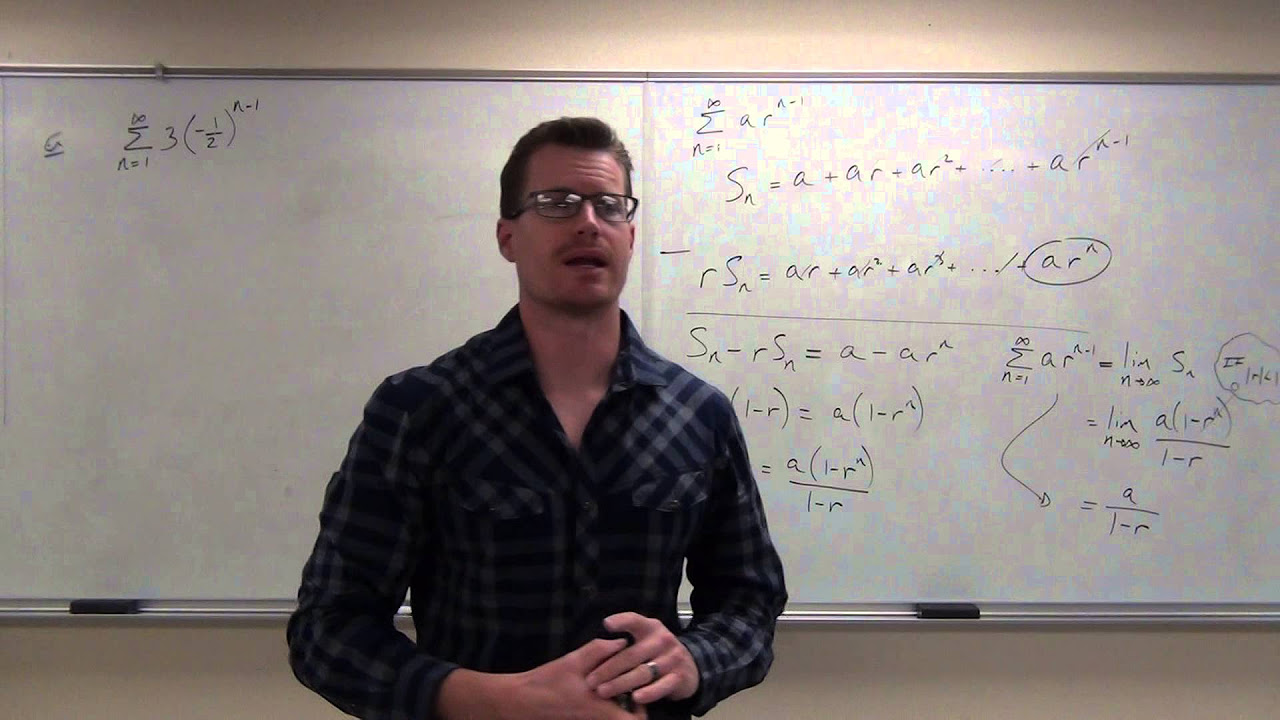
Calculus 2 Lecture 9.2: Series, Geometric Series, Harmonic Series, and Divergence Test

Related Tags

Sequences Series Calculus Mathematics Patterns General Terms Recursive Fibonacci Summation Notation Partial Sums