Differentials
TLDRThe video script presents a comprehensive lesson on differentials, which are essentially components of slope. It begins with a general discussion on slope, explaining how it represents the change in y values with respect to the change in x values over a closed interval. The concept of derivatives is introduced as a means to approximate the instantaneous slope at a specific point, which is achieved by making the interval between x values infinitely small. The lesson then delves into the separation of the derivative into two components, Dy (differential of Y) and Dx (differential of X), which are used to represent the change in y values with respect to the change in x values. The script provides a formula for calculating the differential of Y, which is the product of the derivative and the differential of X. It further illustrates the process of finding the differential of Y through examples, including a detailed walkthrough of calculating the differential for a given function and interpreting the results. The script concludes with practical applications of differentials in economics, such as marginal analysis for revenue, cost, and profit, and estimating possible errors in measurements, like the volume of a ball bearing. The lesson is designed to help learners understand not only the theoretical aspects of differentials but also their practical implications in real-world scenarios.
Takeaways
- 📈 Differentials are used to represent the components of slope, specifically the change in Y with respect to the change in X (Dy and Dx).
- 🔍 The derivative (dy/dx) of a function represents the instantaneous rate of change, which is the limit of the average rate of change as the interval becomes infinitesimally small.
- ↔️ Differentials allow us to separate the concept of the derivative into two parts, Dy (differential of Y) and Dx (differential of X), which can be helpful in certain calculations.
- 📚 The general formula for the differential of Y (Dy) is the derivative of Y with respect to X (f'(x)) multiplied by the differential of X (Dx).
- 🔢 To find a specific value for Dy, we can use the generic formula for Dy and input the given values for x and Dx.
- 📐 The concept of differentials is applied in various fields like economics for marginal analysis, where it helps in estimating changes in revenue, costs, and profits with respect to changes in the independent variable.
- 🛒 In business, differentials can estimate the change in cost corresponding to an increase in sales, which is useful for decision-making.
- 📉 Differentials can also be used to approximate errors in physical measurements, such as the error in calculating the volume of an object when the dimensions are measured with a degree of uncertainty.
- 💰 An example of using differentials in economics is to approximate the change in revenue when there's a one-unit increase in sales, which can be calculated using the revenue function and the differential of the sales volume.
- 📊 For a given function, the differential of Y can be found by differentiating the function with respect to X and then solving for Dy by multiplying by Dx.
- 🔗 The process of finding differentials is connected to the concept of derivatives, but it involves an additional step of separating the change in Y (Dy) from the change in X (Dx) to understand the rate of change at specific points.
Q & A
What are differentials in the context of calculus?
-Differentials are the components of the slope of a function, representing the change in y values with respect to the change in x values. They are used to approximate the instantaneous rate of change at a specific point as the change in x approaches zero.
How is the concept of slope connected to differentials?
-The concept of slope is connected to differentials through the average rate of change over a closed interval. The slope formula (change in y / change in x) is generalized in differentials as Dy/DX, where Dy is the differential of y and DX is the differential of x.
What does the derivative of a function represent?
-The derivative of a function represents the instantaneous rate of change or the slope of the function at a specific point. It is found by taking the limit of the average rate of change as the interval between x values becomes infinitesimally small.
How do you find the differential of Y, Dy?
-The differential of Y, denoted as Dy, is found by multiplying the derivative of Y with respect to X (f'(X)) by the differential of X (DX). The formula is Dy = f'(X) * DX.
What is the purpose of separating Dy and DX in differentials?
-Separating Dy and DX allows for a clearer understanding of the components of slope and can be convenient for solving for Dy alone in various applications, such as in economics for marginal analysis or in approximating errors in physical measurements.
How can differentials be used in economics?
-In economics, differentials are used for marginal analysis to find changes in revenues, costs, and profits with respect to changes in the independent variable, often representing a change in quantity or price.
What is the formula for the differential of Y in terms of the derivative and the differential of X?
-The formula for the differential of Y (Dy) in terms of the derivative (f'(X)) and the differential of X (DX) is Dy = f'(X) * DX.
How can you use differentials to approximate the change in cost corresponding to an increase in sales?
-You can use differentials to approximate the change in cost by finding the derivative of the cost function with respect to the number of sales units, then multiplying this derivative by the change in the number of sales units (DX) to find the differential of cost (DC).
What is the role of differentials in approximating the error in physical measurements?
-Differentials can be used to estimate the possible error in calculated quantities, such as the volume of an object, when there is a small possible variation (error) in the measurements of the object's dimensions.
How does the change in a function's independent variable (DX) relate to the change in the function's value (Dy)?
-The change in the function's value (Dy) is approximated by the product of the function's derivative at a specific point and the change in the independent variable (DX). This relationship is used to estimate the change in the function's output for a small change in its input.
What is the significance of calculating the percent change in profit when production levels change?
-Calculating the percent change in profit provides a relative measure of the impact of the production level change on the total profits. It helps in understanding the significance of the change in profits in comparison to the original profit amount, which is useful for business decisions and financial analysis.
Outlines
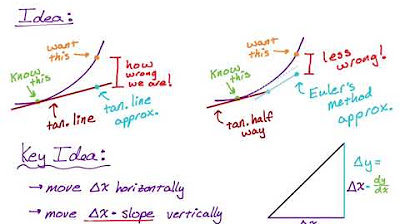
📈 Introduction to Differentials and Slope
The video begins with an introduction to differentials, which are components of slope. The instructor relates differentials to the concept of slope, explaining how the slope of a function represents the change in Y values with respect to the change in X values over a closed interval. The formula for slope is discussed, and the idea of the average rate of change is introduced. The lesson then transitions into derivatives, which are used to approximate the instantaneous slope at a specific point. The process of taking the limit as the interval becomes infinitesimally small to find the instantaneous rate of change is explained. Finally, the concept of separating the derivative into its components, Dy (differential of Y) and DX (differential of X), is introduced, with a focus on finding the differential of Y.
🔢 Calculating Differentials of Y
The second paragraph delves into calculating the differential of Y, which involves finding a generic formula for Dy in terms of the derivative of Y with respect to X and the differential of X. The process of evaluating this formula at a specific point to get a numeric value for the differential of Y is explained. An example is provided where the differential of Y for a given function Y = 2x^3 - 5x is calculated. The derivative is found, and then the differential is computed by multiplying the derivative by the differential of X (DX). The example concludes with an interpretation of the result, explaining how the change in Y relates to the change in X.
🧮 Differentials and Their Application
The third paragraph discusses the application of differentials in practical problems. It begins with an example of finding the differential of Y for a function involving a square root and an exponent. The derivative is calculated using the power rule and chain rule, and then the differential of Y is found by multiplying the derivative by the differential of X. Given values for X and DX, the differential of Y is computed numerically. The paragraph concludes with an emphasis on the utility of differentials in understanding how Y changes over an interval when X changes.
📉 Marginal Analysis and Error Estimation
The fourth paragraph introduces the concept of marginal analysis, which involves using differentials to estimate changes in quantities such as revenue, profit, and cost with respect to changes in an independent variable. The paragraph also touches on the use of differentials for estimating errors in physical quantities, such as the area of a rectangle when the side length measurement is not perfectly accurate. The importance of understanding the practical applications of differentials is highlighted.
💰 Economic Applications of Differentials
The fifth paragraph focuses on the economic applications of differentials, particularly in the context of cost functions. It illustrates how to use differentials to approximate the change in cost corresponding to an increase in sales of one unit. The process involves finding the derivative of the cost function with respect to the sales variable, then using this to calculate the differential of the cost. An example with a given cost function is worked through, showing how to find the differential of cost and interpret the result in economic terms.
📊 Linear Demand Function and Revenue
The sixth paragraph presents a problem involving a linear demand function and the calculation of revenue. The demand function is derived from two points representing different sales volumes and prices. The revenue function, which is the product of sales volume (X) and price (P), is then formulated. The paragraph concludes with an example of how to approximate the change in revenue for a one unit increase in sales when X equals 175, using the derivative of the revenue function.
📈 Profit Approximation and Percent Change
The seventh paragraph explores the use of differentials to approximate changes in profit when the production level changes from 50 to 51 units. The profit function is given, and its derivative is calculated to find the differential of profit (DP). The change in profit is then computed for the specified change in production level. Additionally, the paragraph shows how to calculate the percent change in profit, providing a method to understand the change in profit relative to the total profit.
🔍 Estimating Errors in Measurements
The eighth paragraph discusses the use of differentials to estimate possible errors in measurements, using the example of calculating the volume of a ball bearing with a given radius. The process involves finding the derivative of the volume formula with respect to the radius and then using this to approximate the change in volume (DV) for a possible error in the radius measurement. The calculation is performed, and the potential error in the volume is expressed as a plus or minus value.
📝 Summary and Offer for Help
The final paragraph provides a brief summary of the concepts covered in the video and offers additional help to viewers who may need it. The instructor emphasizes that the process involves separating components of derivatives, which is an extension of concepts already discussed. The video concludes with a sign-off until the next lesson.
Mindmap
Keywords
💡Differentials
💡Slope
💡Derivatives
💡Instantaneous Rate of Change
💡Marginal Analysis
💡Error Estimation
💡Chain Rule
💡Quotient Rule
💡Power Rule
💡Linear Demand Function
💡Profit Function
Highlights
Differentials are components of slope that can be separated into the differential of Y (Dy) and the differential of X (DX).
The concept of slope is introduced as the change in Y values with respect to the change in X values over a closed interval.
Derivatives are used to approximate the instantaneous slope or rate of change at a specific point by making the interval between X values infinitely small.
The generic formula for the differential of Y (Dy) is found by multiplying the derivative of Y with respect to X by the differential of X (DX).
The differential Dy can be used to approximate the change in Y for a given change in X at a specific point on a function.
An example is given where Y = 2x^3 - 5x, and the differential of Y is calculated at X = -2 with a change in X (DX) of 0.1, resulting in a Dy of 1.9.
The differential Dy provides the change in Y values as X increases or decreases from a starting value over a specified interval.
The concept of marginal analysis is introduced, which uses differentials to estimate changes in quantities such as revenue, profit, or cost with respect to changes in an independent variable.
An example of marginal analysis is provided, where the change in cost (DC) for a unit increase in sales is calculated using the differential of the cost function at X = 10 with a change in X (DX) of 1.
The revenue function is derived from a given demand function, and the change in revenue (Dr) for a one-unit increase in sales is approximated at X = 175.
The profit function is used to approximate the change in profit (DP) and the percent change in profit when the production level changes from 50 to 51 units.
Differentials are also used to estimate possible errors, such as in calculating the volume of a ball bearing when the radius measurement has a possible error of 0.1 inch.
The potential error in the volume of the ball bearing is calculated to be plus or minus 0.6158 cubic inches, demonstrating how differentials can estimate errors in physical quantities.
The application of differentials in practical situations such as economics and physics is emphasized to show their utility beyond theoretical mathematics.
The process of finding the differential of Y involves differentiating the function with respect to X and then solving for Dy by multiplying by DX.
The concept of differentials is applicable in various fields, including economics for marginal analysis and in physics for estimating errors in measurements.
The use of differentials to approximate changes in functions is illustrated through multiple examples, including cost, revenue, profit, and physical measurements like volume.
The importance of understanding both the calculation of differentials and their practical applications is stressed for a comprehensive grasp of the subject.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: