Washer method rotating around vertical line (not y-axis), part 1 | AP Calculus AB | Khan Academy

Khan Academy
9 Jan 201307:50
EducationalLearning
32 Likes 10 Comments

TLDRThis video script outlines the process of calculating the volume of a complex shape created by rotating a region between two curves around a vertical line. The method involves using the washer method to integrate with respect to y, setting up an integral over the interval where the curves intersect. The explanation is detailed, providing a step-by-step approach to finding the area of the washers and calculating their volume, ultimately summing them up to find the total volume of the rotated shape.

Takeaways
  • πŸ“ The video discusses calculating the volume of a solid formed by rotating a region between two curves around a vertical axis.
  • πŸ”„ The region to be rotated is bounded by y=√x and y=x^2, and the rotation occurs around the vertical line x=2.
  • 🎨 The resulting shape is a hollowed-out solid with the walls formed by the region between the two curves.
  • πŸ₯³ The method used to find the volume is the washer method, a variant of the disk method, which is suitable for volumes involving rotation around a vertical axis.
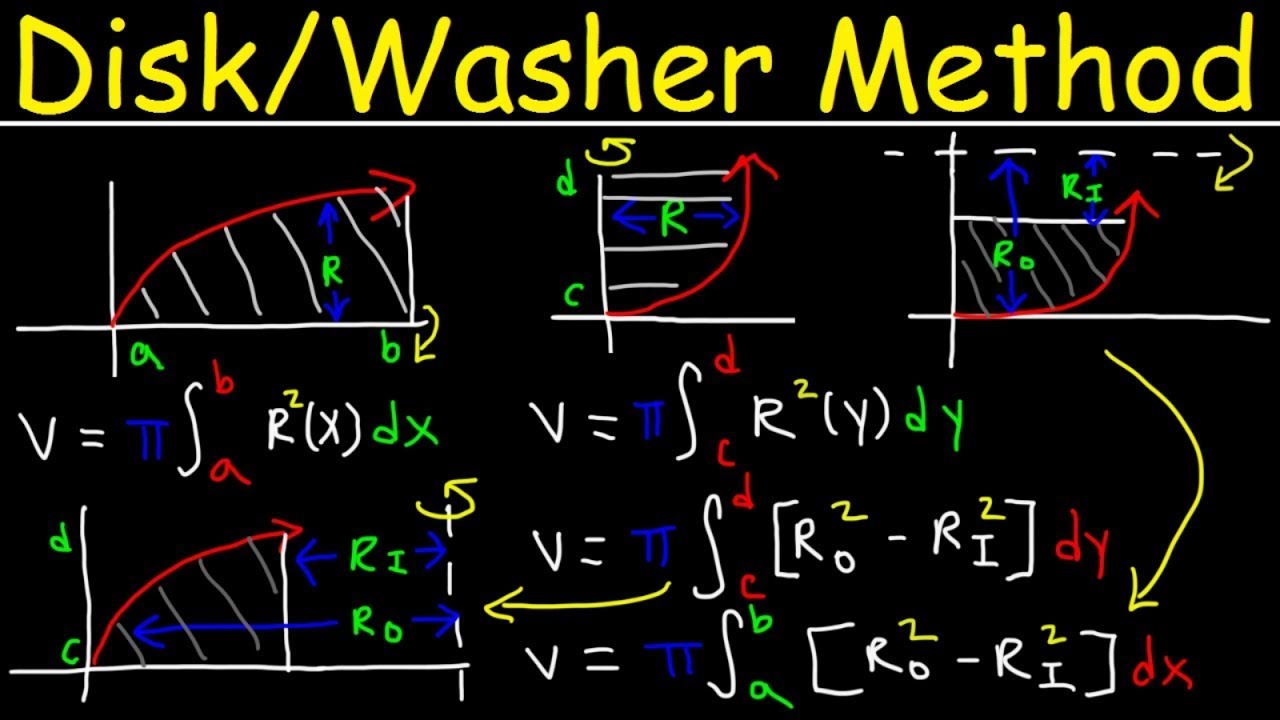
  • πŸ“Š To apply the washer method, the problem is approached by integrating with respect to y, using stacked rings in the y direction.
  • πŸ“ˆ The volume of a single ring is determined by finding the area of the outer and inner circles and calculating the difference.
  • πŸŒ€ The outer radius of a ring is given by the function 2 - y^2, derived from the curve y=√x.
  • πŸŒ€ The inner radius of a ring is given by the function 2 - √y, derived from the curve y=x^2.
  • πŸ”’ The area of a ring is calculated as Ο€ times the difference of the squares of the outer and inner radii.
  • πŸ“š The volume of each ring is found by multiplying the area of the ring by the infinitesimal height dy.
  • 🏞 The total volume of the solid is obtained by integrating the volume of the individual rings over the interval from y=0 to y=1, where the curves intersect.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is calculating the volume of a shape formed by rotating the region between two curves, y=sqrt(x) and y=x^2, around a vertical line x=2 using the washer method.

  • What are the two curves involved in creating the shape?

    -The two curves involved are y=sqrt(x) and y=x^2.

  • Around which vertical line is the region rotated?

    -The region is rotated around the vertical line x=2.

  • What method is used to calculate the volume of the shape?

    -The washer method is used to calculate the volume of the shape.

  • How is the volume of a single ring calculated?

    -The volume of a single ring is calculated by finding the area of the surface of the ring (which is the area of the outer circle minus the area of the inner circle) and multiplying it by its height (an infinitesimal change in y, dy).

  • What is the outer radius of a ring as a function of y?

    -The outer radius of a ring as a function of y is 2 - y^2.

  • What is the inner radius of a ring as a function of y?

    -The inner radius of a ring as a function of y is 2 - sqrt(y).

  • What is the expression for the area of one of the washers?

    -The expression for the area of one of the washers is pi * (outer radius squared) - pi * (inner radius squared), where the outer radius is (2 - y^2) and the inner radius is (2 - sqrt(y)).

  • What is the interval over which the rings are summed up?

    -The interval over which the rings are summed up is from y=0 to y=1, where the two curves intersect.

  • How is the volume of the entire shape found?

    -The volume of the entire shape is found by integrating the volume of a single ring over the interval from y=0 to y=1.

  • What will be done in the next video?

    -In the next video, the integral set up for the volume of the shape will be evaluated.

Outlines
00:00
πŸ“ Introduction to Calculating Volume of a Rotated Region

The paragraph introduces the concept of calculating the volume of a shape created by rotating a region bounded by two curves around a vertical axis that is not the y-axis. The specific region in focus is defined by the curves y = √x (bottom curve) and y = x^2 (top curve), and it is rotated around the vertical line x = 2. The speaker explains that the resulting shape has a hollowed middle and that the goal is to find the volume of this hollowed-out solid. The method of choice for this problem is the washer method, which involves integrating with respect to y and considering the volume contribution of infinitesimally thin rings or washers stacked along the y-axis.

05:02
πŸ“Š Deriving the Equations for Calculating the Volume

This paragraph delves into the specifics of setting up the integral for the volume calculation using the washer method. The speaker explains how to express the outer and inner radii of the washers as functions of y, which are derived from the equations of the curves. The outer radius is given by 2 - x (where x is a function of y, x = y^2), and the inner radius is 2 - √y. The area of the surface of a washer is calculated by taking the difference between the areas of the outer and inner circles, which is then multiplied by the height of the washer (dy) to get the volume of a single washer. The integral of this volume expression over the interval [0, 1] (where the curves intersect) will yield the total volume of the rotated shape, which will be addressed in a subsequent video.

Mindmap
Keywords
πŸ’‘Curves
Curves in this context refer to the mathematical functions y = sqrt(x) and y = x^2, which are being used to define a region. These curves are essential to the video's theme as they outline the area that will be rotated to form the volume of interest. The script describes how the region between these two curves is rotated around a vertical line to create a 3D shape.
πŸ’‘Rotation
Rotation in this context refers to the geometric operation of turning a shape around a point or an axis, resulting in a new shape or position. In the video, the region between the two curves is rotated around the vertical line x = 2 to form a 3D shape with a hollowed-out middle. This process is central to the video's theme of calculating the volume of a solid of revolution.
πŸ’‘Volume
Volume is the measure of the amount of space occupied by a solid object. In the video, the focus is on calculating the volume of the 3D shape formed by rotating the region between the two curves around the vertical line x = 2. The volume is a key concept as it is the ultimate quantity the video aims to find.
πŸ’‘Disk Method
The Disk Method, also known as the Ring Method or Washer Method, is a technique used in calculus to find the volume of a solid of revolution by considering it as made up of infinite thin disks or rings. In the video, this method is chosen to calculate the volume of the shape created by the rotation because the axis of rotation is a vertical line, not the y-axis.
πŸ’‘Integration
Integration is a fundamental concept in calculus that involves finding the antiderivative of a function and using it to calculate areas, volumes, or other accumulated quantities. In the video, integration is the process by which the volume of the shape is determined by summing up the volumes of infinitesimally thin rings created by the rotation of the region between the curves.
πŸ’‘Inner and Outer Radius
Inner and outer radius refer to the distances from the axis of rotation to the inner and outer edges of the rings formed during the rotation process. These radii are crucial in calculating the volume of the washers, which are then summed up to find the total volume of the shape. The script explains how to determine these radii as functions of y to apply in the volume calculation.
πŸ’‘Area of Rings
The area of rings, or washers, is the surface area of the individual thin slices of the solid that would be formed if the shape were cut horizontally. In the context of the video, calculating the area of these rings is a step towards finding their volume, which is then integrated over the entire range of the rotation to find the total volume of the solid.
πŸ’‘Infinitesimal Change
Infinitesimal change, often represented as 'dy', refers to an extremely small increment in a variable, approaching zero. In calculus, this concept is used to describe the limit ofεˆ†ε‰² a quantity into increasingly smaller parts. In the video, the height of the rings (dy) is considered infinitesimal as part of the process to calculate the volume using integration.
πŸ’‘Summation
Summation is the process of adding together all the terms of a sequence or collection of numbers. In the context of the video, summation refers to the addition of the volumes of all the infinitesimally thin rings to find the total volume of the rotated shape. This is done through the process of integration, which sums up the contributions of each infinitesimally small ring.
πŸ’‘Interval
Interval, in mathematical terms, refers to a range or a set of numbers lying within certain bounds. In the video, the interval defines the range of y-values over which the curves intersect, which is crucial for setting the limits for the integration process to calculate the volume of the shape.
πŸ’‘Integral
An integral is a mathematical object that represents the accumulated sum of a function over an interval. In the context of the video, the integral is the limit of the summation of the volumes of the rings as the number of rings approaches infinity, which is used to find the volume of the solid formed by the rotation of the region between the curves.
Highlights

The video demonstrates a method for calculating the volume of a solid formed by rotating a region between two curves around a vertical axis.

The specific curves involved are y = sqrt(x) and y = x^2.

The region is rotated around the vertical line x = 2, which is not the y-axis.

The resulting shape is hollowed out in the middle due to the y = x^2 curve.

The method used to calculate the volume is the washer method, a variation of the disk method.

Integration with respect to y is necessary for this problem.

The video describes the process of stacking rings in the y direction to approximate the volume.

Each ring is generated by rotating a rectangle of height dy around the line x = 2.

The volume of a single ring is calculated by finding the difference in areas of outer and inner circles.

The outer radius of a ring is determined by the function 2 - x, where x is a function of y (x = y^2).

The inner radius of a ring is determined by the function 2 - sqrt(y).

The area of a ring is calculated as pi * (outer radius squared - inner radius squared).

The volume of a ring is found by multiplying the area by its height (dy).

The total volume of the solid is obtained by integrating the volume of all rings over the interval from y = 0 to y = 1.

The intersection points of the curves y = sqrt(x) and y = x^2 within the first quadrant are y = 0 and y = 1.

The integral set up in the video will be evaluated in a subsequent video.

Transcripts

Browse More Related Video

Disk & Washer Method - Calculus

Generalizing the washer method | Applications of definite integrals | AP Calculus AB | Khan Academy

Solid of revolution between two functions (leading up to the washer method) | Khan Academy

2011 Calculus AB free response #3 (c) | AP Calculus AB | Khan Academy

Disc method rotating around vertical line | AP Calculus AB | Khan Academy

Disc/Washer Method vs. Shell Method (rotated about different lines)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathematicsVolume CalculationCurve Rotation Washer MethodGeometryIntegrationAnalytical SkillsEducational ContentMath TutorialVertical Axis