Introduction to Related Rates
TLDRThe video script introduces the concept of related rates, beginning with a review of implicit differentiation. It explains how to find derivatives implicitly using the chain rule when dealing with equations that are not explicitly written as a function of x. The importance of distinguishing between dependent and independent variables is emphasized, with x typically being the independent variable. The script then delves into related rates, which involve changes over time, with time being the independent variable and all others being dependent. Through examples, it demonstrates how to calculate the rates of change for dependent variables with respect to time. The summary prepares viewers for applying these concepts to real-world problems in subsequent videos.
Takeaways
- 📘 Implicit differentiation is used when an equation is not explicitly written as y = f(x), and involves using the chain rule to find dy/dx.
- 🔑 When differentiating y to a power, the chain rule is applied by multiplying the power by the derivative of y with respect to x (dy/dx).
- ⚖️ The dependent variable (y) is the one being differentiated in dy/dx, and the independent variable (x) does not require a dy/dx term.
- 🔍 To solve for dy/dx, algebraic manipulation such as factoring can be used to isolate the derivative.
- 📚 Reviewing past content on implicit differentiation can provide a more in-depth understanding of the process.
- 🔄 Understanding the roles of dependent and independent variables is crucial for correctly applying implicit differentiation.
- 📐 The dependent variable is the one that changes with respect to the independent variable, which is often given context in word problems.
- 🧮 Given an implicit function, to determine how one variable changes with respect to another, the derivative of the dependent variable with respect to the independent variable is found.
- 🕒 In related rates problems, the independent variable is always time, and all other variables are dependent on time.
- 📌 When solving related rates problems, it's important to identify which variables are changing over time and how they are related to each other.
- 🔢 To find the rates of change with respect to time (dp/dt and dq/dt), derivatives are taken implicitly treating all variables except time as dependent.
- 📝 The final step in a related rates problem is to algebraically solve for the rates of change of the dependent variables with respect to time.
Q & A
What is the concept of related rates in calculus?
-Related rates is a concept in calculus that deals with the rate of change of multiple quantities with respect to a third variable, often time, where the quantities are related by a given equation.
Why is implicit differentiation necessary?
-Implicit differentiation is necessary when an equation is not explicitly written as a function y = f(x), and we need to find the derivative dy/dx. It allows us to differentiate equations where x and y are mixed together.
What is the role of the chain rule in implicit differentiation?
-The chain rule is used in implicit differentiation to find the derivative of composite functions, especially when dealing with dependent variables like y in dy/dx.
How do you determine the dependent and independent variables in a given equation?
-The dependent variable is the one that changes with respect to the independent variable. In the context of dy/dx, the variable in the numerator (y) is the dependent variable, and the variable in the denominator (x) is the independent variable.
What is the significance of understanding dependent and independent variables in related rates problems?
-Understanding dependent and independent variables is crucial because it helps identify which variables change with respect to time in related rates problems, which is essential for applying the correct differentiation and solving the problem.
How does the process of finding dq/dp differ from finding dp/dt in related rates problems?
-Finding dq/dp involves differentiating an equation with respect to the independent variable p to find the rate at which q changes with respect to p. In contrast, finding dp/dt involves differentiating the same equation with respect to time t to find the rate at which p changes with respect to time.
What is the general approach to solving related rates problems?
-The general approach involves identifying the dependent and independent variables, differentiating the given equation with respect to the independent variable (usually time), and then solving for the desired rates of change (like dp/dt or dq/dt).
Why is time often considered the independent variable in related rates problems?
-Time is often considered the independent variable in related rates problems because many real-world applications involve quantities that change over time, making time a common and convenient reference for these changes.
How do you solve for the rate of change of one variable with respect to time when given an equation and initial conditions?
-First, implicitly differentiate the given equation with respect to time to find the rates of change (dp/dt and dq/dt). Then, use the initial conditions to solve for the specific values of these rates at the given time.
What is the purpose of factoring out terms when solving for dy/dx or dq/dp in an equation?
-Factoring out terms simplifies the equation and helps isolate the term containing the desired rate of change (dy/dx or dq/dp), making it easier to solve for that specific rate.
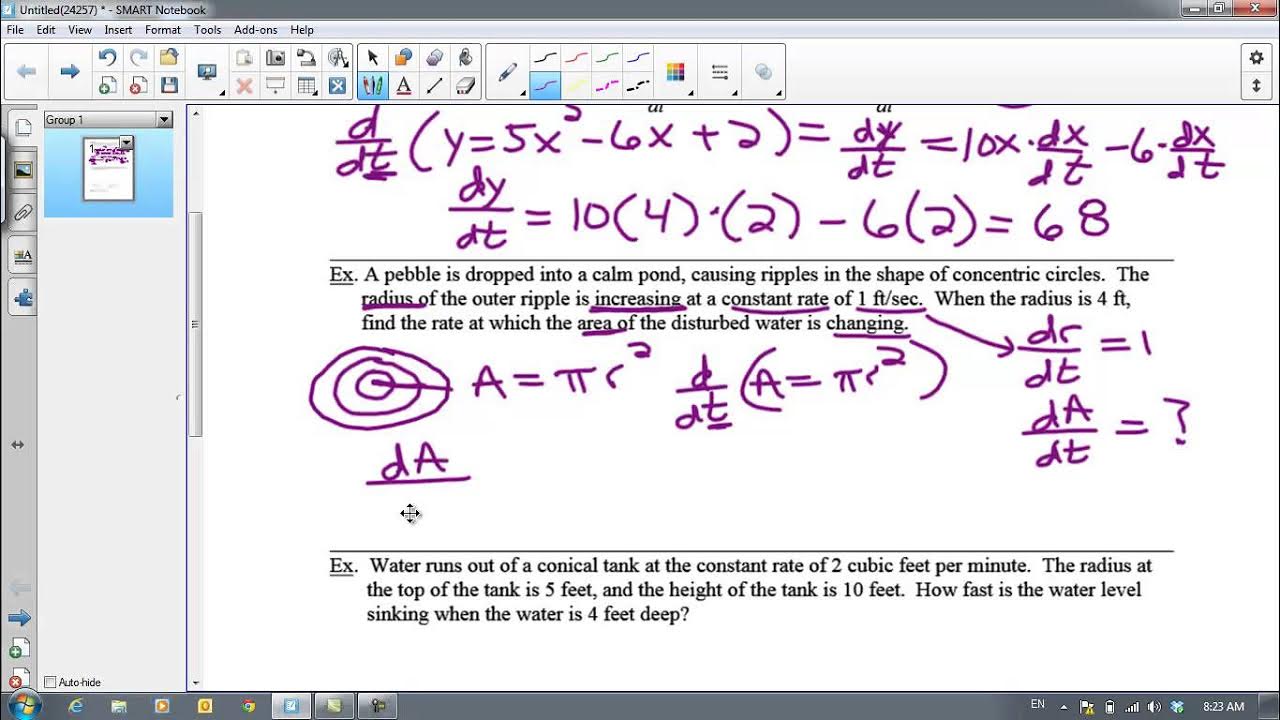
Can you provide an example of a real-world application where related rates might be used?
-An example of a real-world application of related rates is calculating the rate at which the radius of a water balloon expands with respect to time as it is being filled, which can help determine when the balloon will burst.
What is the Leibniz notation, and how does it relate to dependent and independent variables?
-The Leibniz notation, dq/dp, is a way to express the derivative of one quantity with respect to another. In this notation, q is the dependent variable that changes with respect to the independent variable p.
Outlines
📚 Implicit Differentiation Review
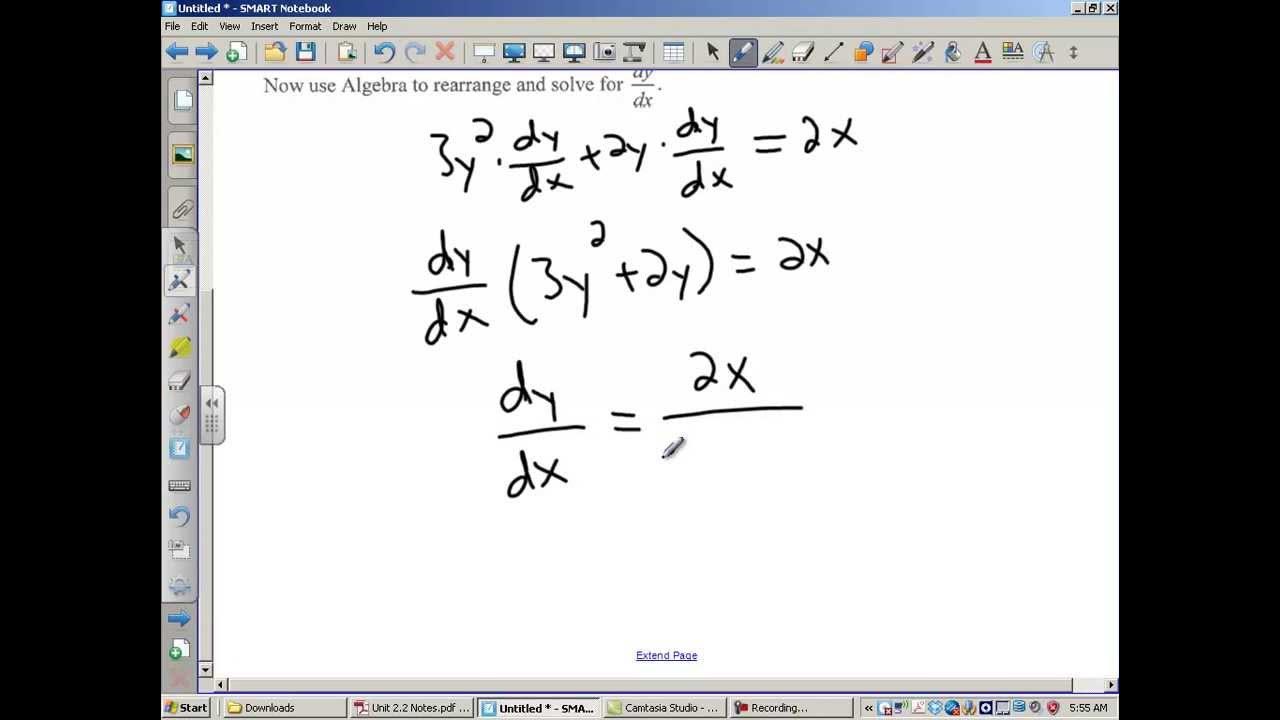
This paragraph introduces the concept of related rates and begins with a review of implicit differentiation. It explains that when an equation is not explicitly written as y = f(x), we need to find the derivative dy/dx implicitly using the chain rule. The example given involves taking the derivative of y^5 and then solving for dy/dx by factoring out terms. The importance of understanding dependent and independent variables is emphasized, with an example problem provided to illustrate how to determine the rate of change of q with respect to p (dq/dp). The paragraph concludes by recommending further review of implicit differentiation through additional resources.
🔍 Identifying Dependent and Independent Variables
The second paragraph focuses on the importance of identifying dependent and independent variables when performing implicit differentiation. It clarifies that the dependent variable is the one in the numerator of the derivative dy/dx, and the independent variable is the one in the denominator. The paragraph uses an example to show how to take the derivative of an implicit function to find dq/dp. It then transitions into discussing related rates, which involve changes over time. The independent variable in related rates problems is always time, with all other variables being dependent. An example is given to find the rates of change of p and q with respect to time (dp/dt and dq/dt), emphasizing the need to treat all variables in the equation as dependent when differentiating with respect to time.
🕒 Solving for Rates of Change Over Time
The final paragraph builds on the previous discussions to solve for rates of change over time in a related rates problem. It outlines the process of differentiating the given equation with respect to time, treating all variables as dependent. The paragraph provides the steps to find dp/dt and dq/dt, resulting in expressions that include these rates. It concludes by setting the stage for applying these concepts to an application problem in the next video, which will involve using the derived rates of change to solve a real-world scenario.
Mindmap
Keywords
💡Related Rates
💡Implicit Differentiation
💡Chain Rule
💡Dependent Variable
💡Independent Variable
💡Derivative
💡Leibniz Notation
💡Business Applications
💡Time
💡Algebraic Manipulation
💡Word Problem
Highlights
Introduction to the concept of related rates
Review of implicit differentiation
Using the chain rule for implicit differentiation
Derivative of y to the fifth using the chain rule
Solving for dy/dx using algebraic manipulation
Understanding dependent and independent variables
Determining which variable is dependent using the problem statement
Example of finding dq/dp for an implicit function
Related rates involve changes over time
In business applications, quantities like revenue, profit, costs, quantity, and price change over time
The independent variable in related rate problems is always time
Example of finding dp/dt and dq/dt for an equation involving p and q
Treating p and q as dependent variables when differentiating with respect to time
Solving for dp/dt and dq/dt using algebraic manipulation
Importance of knowing the dependent and independent variables in related rate problems
Next video will apply related rates to an application problem
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: