Squeeze/Sandwich Theorem
TLDRThis video provides an engaging explanation of the Squeeze Theorem, also known as the Sandwich Theorem, using the analogy of a sandwich to illustrate the concept. The presenter explains that to apply the theorem, one must find an upper and lower bound for a function, ensuring the function is always between these bounds. The focus of the video is on a limit as 'x' approaches zero for a function involving 'x' in the denominator, which cannot be directly evaluated using L'Hôpital's rule. The video guides viewers through the process of applying the Squeeze Theorem by identifying the bounds of the function, which in this case are the sine function and its exponential counterpart. By carefully constructing the 'sandwich' and taking the limit as 'x' approaches zero, the presenter demonstrates that the limit of the function is zero. The video concludes with an encouragement to never stop learning, emphasizing the importance of continuous education.
Takeaways
- 📚 The video is an educational resource aimed at explaining the Squeeze Theorem, also known as the Sandwich Theorem or the Two Policemen Chasing a Criminal Theorem.
- 🔢 It begins with an introduction to limits, particularly emphasizing situations where direct substitution in a function is not possible due to indeterminate forms (e.g., division by zero).
- 👨💻 The speaker employs common analogies to make the theorem more relatable and easier to understand, comparing it to constructing a sandwich.
- 🔨 The main goal of the Squeeze Theorem is described: to trap the target function between two bounding functions that converge to the same limit.
- 📱 Different parts of a complex function are analyzed to determine which parts can be bounded effectively, focusing primarily on the behavior of trigonometric functions like the sine function.
- 📡 An example is worked through where the function involves exponential and polynomial components, illustrating how to apply the theorem in practical scenarios.
- 🔥 The video details how to establish upper and lower bounds using properties of exponential functions and inequalities, ensuring that these bounds are finite and converge.
- 👏 The speaker provides a walkthrough of how to formalize the squeezing of the function step-by-step, reinforcing learning with visual and verbal metaphors.
- 📍 By the end, a limit is calculated using the established bounds, demonstrating the theorem’s utility in solving limit problems where direct evaluation is challenging.
- 💎 The video concludes with a strong educational message encouraging continuous learning, tying back to the practical and philosophical value of the mathematical concepts discussed.
Q & A
What is the Squeeze Theorem, also known as the Sandwich Theorem?
-The Squeeze Theorem is a method for finding the limit of a function as the input approaches a certain value. It involves bounding the function between two other functions for which the limit is known, and then showing that the limit of the original function must be the same as the common limit of the bounding functions.
Why is the Squeeze Theorem useful when dealing with limits that are not directly computable?
-The Squeeze Theorem is useful in situations where direct computation of a limit is not possible, such as when the function is undefined at the point of interest. By bounding the function between two other functions with known limits, we can deduce the limit of the original function without direct computation.
What is the role of the exponential function e in the context of the provided script?
-In the script, the exponential function e is used to create an upper and lower bound for the function sin(1/x) as x approaches zero. Since e raised to any real number is always positive, it helps to establish bounds that are always greater than or equal to zero, which is crucial for applying the Squeeze Theorem.
How does the sign function affect the bounds in the Squeeze Theorem?
-The sign function, which returns -1, 0, or 1 depending on whether the input is negative, zero, or positive, respectively, is used to set the bounds for the exponential function in the script. It ensures that the bounds are always between -1 and 1, which is a critical step in constructing the 'sandwich' for the theorem.
What is the significance of x^2 being always positive in the context of the Squeeze Theorem?
-The factor x^2 is significant because it is always non-negative, even when x approaches zero. This property allows it to be safely multiplied by the exponential terms without changing the sign of the inequality, thus maintaining the integrity of the bounds for the Squeeze Theorem.
Why is it not possible for the limit of the function in the script to be less than zero?
-According to the Squeeze Theorem, if both the lower and upper bounds of the function have a limit of zero as x approaches the point of interest, then the limit of the function itself must also be zero. It cannot be less than zero because both bounds are non-negative, making it impossible for the function to be negative.
What is the analogy used in the script to help understand the Squeeze Theorem?
-The analogy used in the script is that of a sandwich, where the function whose limit is being sought is the 'meat' and the bounding functions are the 'bread'. The idea is that if the 'meat' is squeezed between two pieces of 'bread', and the 'bread' has the same 'taste' (limit), then the 'meat' must also have that 'taste' (limit).
How does the script handle the issue of the function being undefined at x = 0?
-The script addresses the issue by not attempting to directly substitute x = 0 into the function, which would be undefined due to division by zero. Instead, it uses the Squeeze Theorem to find the limit by bounding the function with other functions that are defined at x = 0.
What is the role of the constant e in establishing the bounds for the Squeeze Theorem?
-The constant e is used as the base for the exponential function in the bounds. Since e^x is always positive for any real number x, it ensures that the bounds are also positive, which is necessary for the application of the Squeeze Theorem.
Why does the script mention that raising a number to an exponential function does not make it negative?
-The script mentions this to emphasize that the exponential function e^x is always positive, regardless of the value of x. This property is important for maintaining the non-negativity of the bounds in the Squeeze Theorem, ensuring that the inequality signs remain consistent.
What is the final conclusion of the script regarding the limit of the given function as x approaches zero?
-The final conclusion of the script, using the Squeeze Theorem, is that the limit of the function x^2 * e^(sin(1/x)) as x approaches zero is equal to zero.
Outlines
😀 Introduction to the Squeeze Theorem
The video begins with an introduction to the Squeeze Theorem, also known as the Sandwich Theorem. It addresses the audience who may not fully understand this concept, those who enjoy watching the presenter's videos, and those who may have forgotten the theorem. The presenter explains the theorem's application to a limit as X approaches zero for a function that cannot be directly evaluated at zero due to being in the denominator. The Squeeze Theorem is introduced as a method to set bounds on the function, ensuring it is always less than an upper bound and greater than a lower bound, which ultimately converge to the same value.
📚 Applying the Squeeze Theorem to a Function
The presenter continues by illustrating how to apply the Squeeze Theorem to a specific function. They discuss the need to find an upper and lower bound for the function and use the properties of the exponential function e^x, which is always positive. The video emphasizes the importance of maintaining the sign of the function while applying the theorem. It shows how to construct the bounds by considering the sign of the function and the fact that x^2 is always non-negative. The presenter then demonstrates how to combine these elements to form the 'sandwich' and take the limit as X approaches zero, showing that the limit of the function is zero.
🎓 Conclusion and Final Thoughts on the Squeeze Theorem
In the final paragraph, the presenter concludes the explanation of the Squeeze Theorem by reiterating that the limit of the given function as X approaches zero is zero. They emphasize the logical process of elimination used in the theorem to determine that the limit cannot be negative and must be zero. The video ends with an encouraging message to the audience to never stop learning, highlighting the importance of continuous education.
Mindmap
Keywords
💡Squeeze Theorem
💡Limit
💡Exponential Function
💡Denominator
💡Undefined
💡L'Hôpital's Rule
💡Bounds
💡Positive
💡Infinity
💡Analogies
💡Continuous Function
Highlights
The video provides a comprehensive explanation of the Squeeze Theorem, also known as the Sandwich Theorem.
The Squeeze Theorem is used to find limits of functions where direct substitution is not possible, particularly when the function is undefined at the point of interest.
The theorem involves finding an upper and lower bound ('bread') for the function in question ('meat') between which it is 'sandwiched'.
The function considered in the video is e^(sin(1/x)), which is undefined at x=0 due to the denominator.
The presenter uses the analogy of a sandwich to explain the concept, where the bread represents the bounds and the meat represents the function.
The smallest value that x^2 can take is zero, and it is always positive.
The sign of any number is always between -1 and 1, which can be used as bounds for the sine function in the given example.
The presenter emphasizes that exponential functions, such as e^x, are always positive, which helps in maintaining the inequality signs.
The video demonstrates how to apply the Squeeze Theorem step by step to the function e^(sin(1/x)) as x approaches zero.
The limits of the bounds as x approaches zero are calculated to be zero, providing the bounds for the original function.
By the Squeeze Theorem, if the bounds have the same limit, the function itself must also have that limit.
The final result of applying the Squeeze Theorem to the given function is that the limit is zero as x approaches zero.
The video concludes with the presenter reminding viewers to never stop learning as a way to continuously grow and understand complex mathematical concepts.
The use of relatable analogies, such as a sandwich, makes the concept of the Squeeze Theorem more accessible to a wider audience.
The presenter also cautions about the importance of maintaining the signs in inequalities when applying the theorem.
The video provides a clear demonstration of how to handle limits where L'Hôpital's Rule is not applicable.
The presenter explains the concept in a way that is both informative and engaging, making the video educational and entertaining.
The video is a valuable resource for those who wish to understand the Squeeze Theorem in the context of limits and mathematical analysis.
Transcripts
Browse More Related Video

Squeeze Theorem for Limits (1)

Finding limits at infinity using squeeze theorem | Squeeze or Sandwich Theorem - Calculus
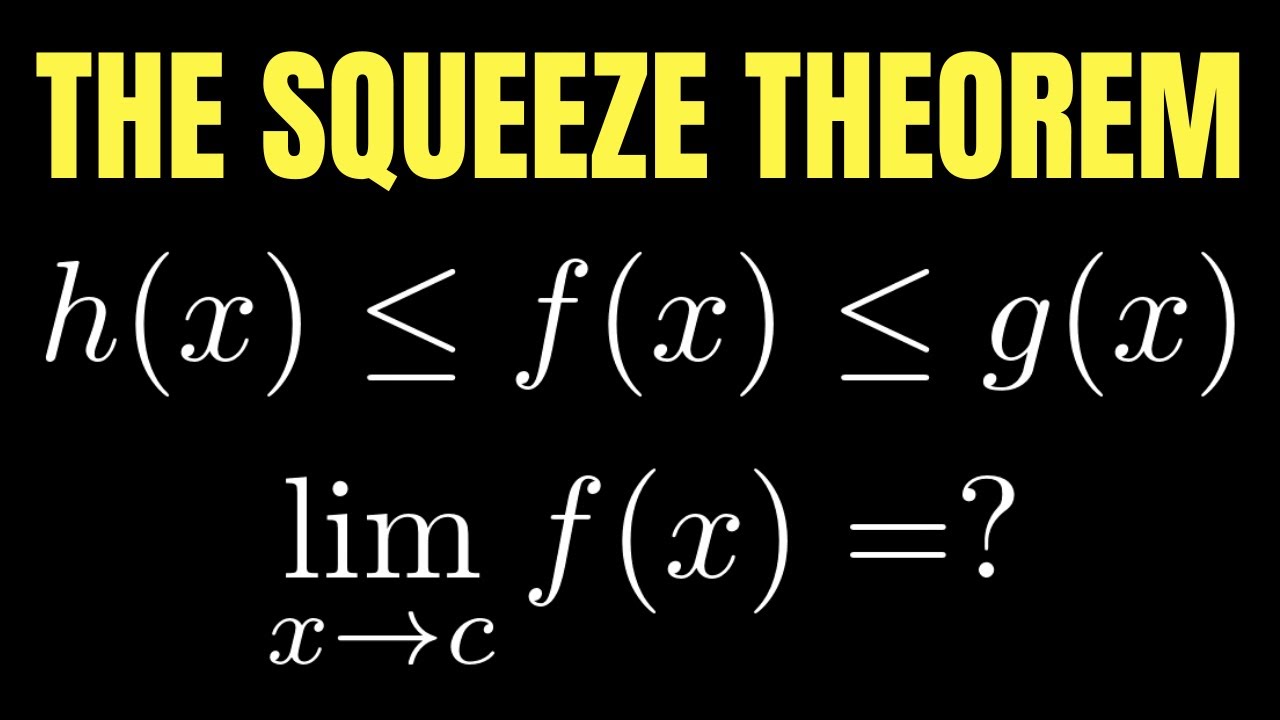
Calculus: The Squeeze Theorem Full Tutorial
Limits of Oscillating Functions and the Squeeze Theorem

Limit of x! over x^x as x goes to infinity

Calculus AB/BC – 1.8 Determining Limits Using the Squeeze Theorem
5.0 / 5 (0 votes)
Thanks for rating: