Limits and Their Properties

Chad Gilliland

26 Aug 201306:54

EducationalLearning

32 Likes 10 Comments

TLDRThis calculus video tutorial focuses on the concept of limits and their properties. The instructor explains how to apply different limit rules, such as the constant multiple and quotient rules, using examples to illustrate the process. Special trigonometric limits are demonstrated graphically, emphasizing the importance of approaching values from both sides. The video also covers indeterminate forms and the squeeze theorem, providing algebraic and graphical insights into solving limit problems. The session concludes with the promise of more practice in the next class.

Takeaways

📚 The video is a calculus lesson focusing on limits and their properties.
📈 The instructor references a table of limit properties but does not read it, instead opting to go through examples.
🔢 The first example demonstrates the use of the constant multiple rule (rule number five) to find the limit of a function as X approaches a.
🎯 The limit of 5 × G(X) as X approaches a is found by multiplying the limit of G(X) by 5, resulting in 15.
📉 In the second example, the quotient rule for limits is applied to find the limit of a ratio of two functions as X approaches a, yielding 2/3.
📊 The instructor uses graphical illustrations to explain two special trigonometric limits, showing how the values approach 1 and 0 as θ approaches 0.
🚫 The script clarifies that an indeterminate form, such as 0/0, does not mean the limit is undefined but requires further work to find the actual limit.
🔍 The video includes an example of how to manipulate an expression to match known limits, such as multiplying by a factor to simplify the expression.
📐 The instructor explains how to handle limits involving monomials and polynomials by separating them and evaluating each part individually.
🤏 The squeeze theorem is introduced as a method to find limits when direct evaluation is not possible, by 'squeezing' the function between two known functions.
📚 The lesson concludes with a reminder that students will practice limit problems in the next class.

Q & A

What is the first property of limits discussed in the video?
-The first property discussed is the constant multiple rule, which states that the limit of a constant times a function as x approaches a point is equal to the constant times the limit of the function as x approaches that point.
What is the limit of f(x) as x approaches 'a' given that the limit is 2?
-The limit of f(x) as x approaches 'a' is 2, meaning as x gets closer to 'a', the value of f(x) gets closer to 2.
What is the limit of G(x) as x approaches 'a' in the given example?
-The limit of G(x) as x approaches 'a' is 3, indicating that as x approaches 'a', the value of G(x) approaches 3.
How is the limit of 5 * G(x) as x approaches 'a' calculated using the constant multiple rule?
-The limit of 5 * G(x) as x approaches 'a' is calculated by taking 5 times the limit of G(x) as x approaches 'a', which is 5 * 3 = 15.
What is the quotient rule for limits and how is it applied in the video?
-The quotient rule for limits states that the limit of a quotient of two functions as x approaches a point is equal to the quotient of the limits of the numerator and denominator functions as x approaches that point. In the video, it is applied by taking the limit of f(x) over the limit of G(x) as x approaches 'a', resulting in 2/3.
What are the two special trigonometric limits discussed in the video?
-The two special trigonometric limits discussed are sin(x)/x as x approaches 0, which equals 1, and (1 - cos(x))/x as x approaches 0, which equals 0.
Why does the limit of sin(x)/x as x approaches 0 equal 1?
-The limit of sin(x)/x as x approaches 0 equals 1 because both the left and right limits approach 1, and since they match, the overall limit is 1.
What is an indeterminate form and why does it occur in the example of (1 - cos(x))/x as x approaches 0?
-An indeterminate form occurs when an expression results in 0/0 or similar undefined expressions. In the example of (1 - cos(x))/x, as x approaches 0, the expression results in 1 - 1 (since cos(0) = 1) divided by 0, which is an indeterminate form. However, the graphical approach shows that the limit is actually 0.
How can you use properties of limits to evaluate the limit of (sin(5x))/(5x) as x approaches 0?
-By factoring out a 1/5 from the expression, you can rewrite the limit as (1/5) * (sin(5x)/5x). Since the limit of sin(x)/x as x approaches 0 is 1, the overall limit becomes (1/5) * 1, which is 1/5.
What is the squeeze theorem and how is it demonstrated in the video?
-The squeeze theorem is a method used to find the limit of a function when direct substitution results in an indeterminate form. In the video, it is demonstrated by showing that if a function f(x) is always between two other functions, and those two functions have the same limit as x approaches a certain point, then f(x) must also have that limit.
How does the video use the squeeze theorem to find the limit of an unknown function f(x) that is always between 2 and x^2 + 2?
-The video uses the squeeze theorem by showing that since f(x) is always between the two functions y = 2 and y = x^2 + 2, and both of these functions have the limit of 2 as x approaches 0, f(x) must also have a limit of 2 at that point.

Outlines

00:00

📚 Introduction to Calculus Limits and Properties

This paragraph introduces a Calculus lesson focusing on limits and their properties. The instructor emphasizes the importance of understanding the provided table of properties but chooses not to read it aloud, instead opting to work through examples. The first example involves finding the limit as X approaches a certain value, where two functions, f(x) and G(x), approach specific y-values. The instructor applies the constant multiple rule to find the limit of a function multiplied by a constant. The second example uses the quotient rule for limits, dividing the limits of the numerator and denominator. The paragraph also mentions two special trigonometric limits, which are demonstrated graphically, showing how the limits approach specific values as the variable approaches zero. The instructor clarifies that these graphical representations help confirm the theoretical limits learned in pre-calculus.

05:03

📈 Graphical and Algebraic Approaches to Trigonometric Limits

The second paragraph delves deeper into trigonometric limits, using both graphical and algebraic methods to illustrate the concept. The instructor begins by graphing 'sin x / x' and explains that as the variable approaches zero, the limit is one, despite the function being undefined at that point. This introduces the concept of an indeterminate form, which requires further algebraic manipulation to resolve. The instructor then demonstrates algebraic techniques for resolving such forms, using an example to show how to manipulate the expression to find the limit. The paragraph also covers how to handle limits involving monomials and polynomials separately and concludes with an introduction to the squeeze theorem, a method for finding limits when direct calculation is not possible. The squeeze theorem is illustrated with a graph that shows a function trapped between two known functions, leading to the conclusion that the limit of the unknown function must be the same as the limits of the bounding functions.

Mindmap

Keywords

💡Limit

A limit in calculus is the value that a function or sequence 'approaches' as the input or index approaches some value. In the video, limits are central to understanding the behavior of functions as they approach certain points, such as 'the limit as X approaches a of f(x)'. The script provides examples of calculating limits, such as finding the limit of 5 * G(x) as X approaches a, which is a fundamental concept in the study of calculus.

💡Constant Multiple Rule

The Constant Multiple Rule is a property of limits that states the limit of a constant times a function is equal to the constant times the limit of the function. In the script, this rule is applied when calculating the limit of 5 * G(x) as X approaches a, illustrating how to factor out the constant and simplify the limit calculation.

💡Quotient Rule

The Quotient Rule for limits is a property that allows you to find the limit of a quotient by finding the limit of the numerator and the limit of the denominator separately and then dividing them. The script mentions this rule in the context of finding the limit of f(x)/G(x) as X approaches a, where the limits of f(x) and G(x) are already known.

💡Trig Limits

Trig Limits refer to the limits of trigonometric functions as their input approaches certain values. The script discusses two special trigonometric limits graphically, showing how the values of sin(x)/x and (1 - cos(x))/x approach as the input approaches zero, which are fundamental concepts in understanding the behavior of trigonometric functions at specific points.

💡Indeterminant Form

An indeterminant form in calculus occurs when an expression does not have a well-defined limit, such as 0/0. In the script, the term is used to describe the situation when plugging in 0 for Theta results in 1 - cos(0) divided by 0, which graphically is understood to be zero, but algebraically requires further work to determine the limit.

💡Squeeze Theorem

The Squeeze Theorem is a method in calculus used to find the limit of a function when direct methods are not possible. It involves 'squeezing' the function between two other functions whose limits are known. The script explains this concept by showing a function that is always between two graphs, y = 2 and y = x^2 + 2, and deducing that the limit of the unknown function must be the same as the limit of these two functions, which is 2.

💡Graphical Interpretation

Graphical Interpretation in the context of the script refers to the use of graphs to understand and find limits. The instructor uses graphs to show the behavior of functions as their input approaches certain values, such as sin(x)/x and (1 - cos(x))/x, providing a visual aid to comprehend the concept of limits.

💡Polynomial

A polynomial is an expression consisting of variables and coefficients, involving only the operations of addition, subtraction, multiplication, and non-negative integer exponents of variables. In the script, polynomials are used in the context of limit examples, such as 2x/x, where the limit as X approaches zero is calculated.

💡Monomial

A monomial is a single term algebraic expression, which can be a number, a variable, or the product of numbers and variables raised to whole number powers. The script mentions monomials in the context of dividing by a monomial on the bottom and having the right to separate the limit into two parts, as in the example of 2x/x.

💡Common Denominators

Common denominators are used in fractions to combine them into a single fraction. In the script, the concept is applied when the instructor separates the limit of 2x/x and sin(x)/x, which are then evaluated separately because they have common denominators, simplifying the process of finding the limit.

Highlights

Introduction to Calculus video on limits and their properties.

Reference to a table of properties for limits.

Explanation of the limit as X approaches a of f(x) being 2.

Use of the constant multiple rule for limits.

Calculation of the limit as X approaches a of 5 * G(x).

Application of the quotient rule for limits.

Graphical demonstration of trigonometric limits.

Limit of sin(x)/x as x approaches zero equals one.

Limit of (1 - cos(x))/x as x approaches zero equals zero.

Indeterminate form and its resolution in limits.

Manipulation of limits using properties to simplify.

Separation of limits in a monomial and polynomial.

Evaluation of limits separately for simplified calculations.

Introduction to the squeeze theorem in limits.

Graphical illustration of the squeeze theorem.

Conclusion on the limit of a function using the squeeze theorem.

Anticipation of further limit problems in the next class.

Transcripts

Browse More Related Video

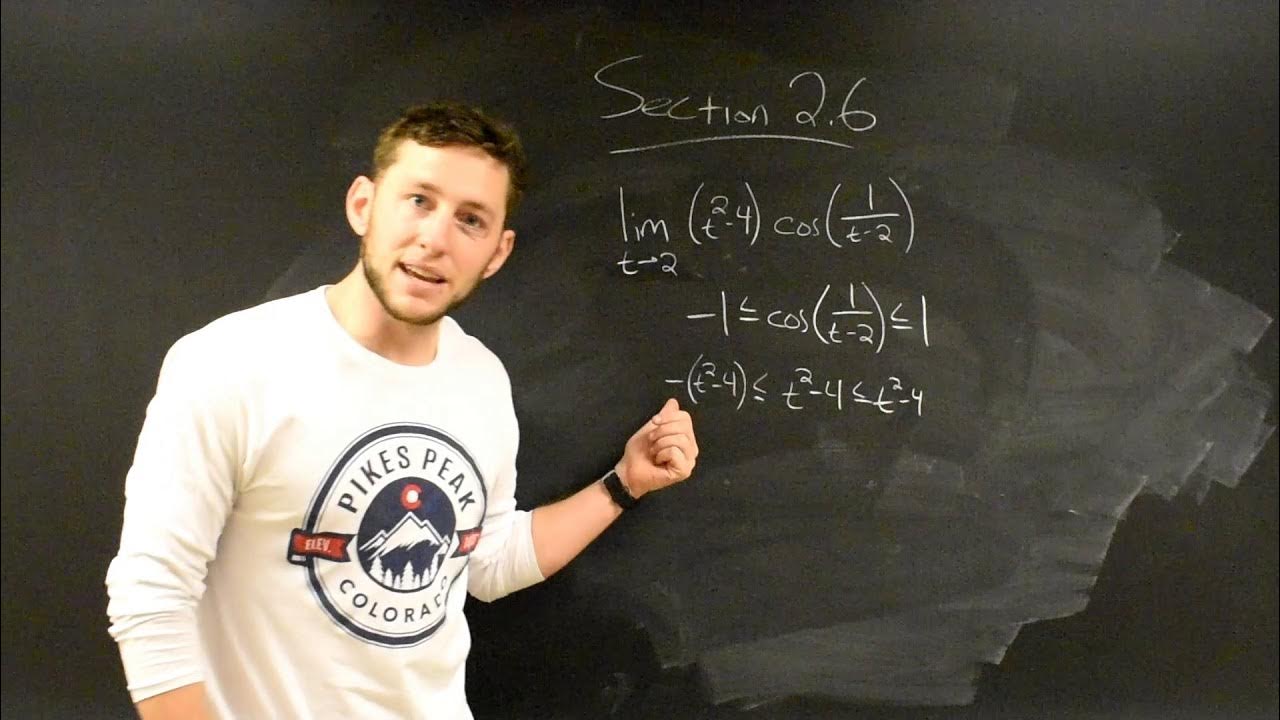
Limits Involving Sine and Cosine & The Squeeze Theorem!

AP Calculus AB: Understanding how to evaluate limits algebraically and analyze limits graphically

One Sided Limits, Graphs, Continuity, Infinity, Absolute Value, Squeeze Thereom - Calculus Review

Calculus AB Homework 1.3 Evaluating Limits

AP Calculus AB - 1.5 Determining Limits Using Algebraic Properties of Limits

AP Calculus AB - 1.6b Determining Limits Using Algebraic Manipulation

Limits and Their Properties

Takeaways

Q & A

What is the first property of limits discussed in the video?

What is the limit of f(x) as x approaches 'a' given that the limit is 2?

What is the limit of G(x) as x approaches 'a' in the given example?

How is the limit of 5 * G(x) as x approaches 'a' calculated using the constant multiple rule?

What is the quotient rule for limits and how is it applied in the video?

What are the two special trigonometric limits discussed in the video?

Why does the limit of sin(x)/x as x approaches 0 equal 1?

What is an indeterminate form and why does it occur in the example of (1 - cos(x))/x as x approaches 0?

How can you use properties of limits to evaluate the limit of (sin(5x))/(5x) as x approaches 0?

What is the squeeze theorem and how is it demonstrated in the video?

How does the video use the squeeze theorem to find the limit of an unknown function f(x) that is always between 2 and x^2 + 2?