How to Convert From Rectangular Coordinates to Polar Coordinates (Precalculus - Trigonometry 38)
TLDRThe video script is an educational guide on converting points between rectangular and polar coordinate systems. It emphasizes the process is straightforward from polar to rectangular due to the clear relationship between radius (r), angle (theta), x, and y coordinates. However, converting from rectangular to polar introduces complexities, as the arctangent function only spans angles from -π/2 to π/2. The script provides a step-by-step method to accurately determine the polar coordinates, including adjusting angles for points in different quadrants by adding π or 2π as necessary. It also addresses the treatment of angles when they fall outside the principal range of the arctangent function, ensuring the correct quadrant is used for the final polar representation. The explanation is supported with examples and highlights the importance of understanding the mathematical reasoning behind the conversion process.
Takeaways
- 📐 **Polar to Rectangular Conversion**: Use the Pythagorean theorem (r = √(x² + y²)) and trigonometric inverses (θ = tan^(-1)(y/x)) to convert polar coordinates (r, θ) to rectangular coordinates (x, y).
- 🔄 **Ambiguity in Reverse Conversion**: Converting rectangular coordinates to polar introduces ambiguity due to the periodic nature of the tangent function, which is only defined from -π/2 to π/2.
- 📍 **Quadrant Considerations**: When converting from rectangular to polar, the quadrant of the point affects the angle θ. For points in quadrants 1 or 4, the angle from tan^(-1) is correct, but for quadrants 2 or 3, add π to the angle.
- ➕ **Adjusting for Positive Angles**: If a positive angle is required and the point is in quadrant 4, add 2π to the angle obtained from tan^(-1) to keep it in the correct quadrant.
- 🤔 **Understanding Tangent Inverse Limitations**: Tangent inverse only provides angles within the range of -π/2 to π/2, which corresponds to quadrants 1 and 4. For other quadrants, adjustments are necessary.
- 😕 **Dealing with Undefined Tangent**: When the tangent function is undefined, such as at y = 0 with x ≠ 0, the angle is either π/2 or 3π/2, and the choice depends on the quadrant of the point.
- 📈 **Plotting the Point First**: Always plot the point on the rectangular coordinate system to determine its quadrant before attempting to find the polar coordinates.
- 🧮 **Using a Calculator for Irregular Values**: For points with non-integer coordinates, use a calculator to find the approximate value of the angle in radians.
- 🤓 **Retaining Exactness**: When possible, retain the exact mathematical form of r (such as √6.1) instead of rounding to a decimal approximation for precision.
- 🔢 **Approximation for Practicality**: In practical scenarios, it may be acceptable to use the approximate decimal value of r (such as 2.47 instead of √6.1) for simplicity.
- ⚙️ **Practical Application**: The process of converting between coordinate systems is essential for understanding different mathematical representations and is useful in fields where polar coordinates are prevalent.
Q & A
What are the two different representations of a point discussed in the video?
-The two different representations of a point discussed in the video are polar coordinates and rectangular coordinates.
How does the Pythagorean theorem relate to changing from rectangular to polar coordinates?
-The Pythagorean theorem states that x squared plus y squared equals r squared. This relationship allows you to calculate the radius (r) by taking the square root of the sum of the squares of x and y.
What is the range of angles that the tangent inverse function typically provides?
-The tangent inverse function typically provides angles in the range from negative pi over two to pi over two.
Why is it necessary to add pi to the angle obtained from tangent inverse when dealing with points in quadrants two or three?
-It is necessary to add pi to the angle obtained from tangent inverse when dealing with points in quadrants two or three because the tangent inverse function only provides angles in quadrants four and one. Adding pi adjusts the angle to the correct quadrant.
How can you determine the quadrant of a point when converting from rectangular to polar coordinates?
-You can determine the quadrant of a point by looking at the signs of the x and y coordinates. The signs will tell you which quadrant the point lies in, which is important for finding the correct angle (theta).
What is the formula used to convert x and y rectangular coordinates into r in polar coordinates?
-The formula used to convert x and y rectangular coordinates into r in polar coordinates is r = sqrt(x^2 + y^2).
What is the significance of the angle theta in polar coordinates?
-The angle theta in polar coordinates signifies the direction of the point from the origin (pole) and is measured in radians or degrees.
Why might you need to add 2 pi to the angle obtained from tangent inverse for points in quadrant four?
-You might need to add 2 pi to the angle obtained from tangent inverse for points in quadrant four if you require a positive angle. This adjustment keeps the angle within the same quadrant but makes it positive.
How does the video script guide viewers to find the angle theta when converting from rectangular to polar coordinates?
-The video script guides viewers to find the angle theta by using the tangent inverse of y over x, and then adjusting the angle based on the quadrant of the point. If the point is in quadrants two or three, pi is added to the angle. If the point is in quadrant four and a positive angle is needed, 2 pi is added.
What is the potential issue with using tangent inverse to find the angle theta for points in quadrants two and three?
-The potential issue with using tangent inverse to find the angle theta for points in quadrants two and three is that tangent inverse will only provide an angle that corresponds to quadrants four and one. Therefore, the angle obtained must be adjusted by adding pi to correctly represent the point's location in the respective quadrant.
How can you ensure that you are correctly converting rectangular coordinates to polar coordinates for points that do not lie on the unit circle?
-For points not on the unit circle, you can ensure correct conversion by first calculating the radius (r) using the Pythagorean theorem, then using a calculator to find the tangent inverse for theta. If the point is not in quadrants four or one, adjust the angle by adding pi or 2 pi as necessary to match the point's quadrant.
Outlines
😀 Introduction to Polar and Rectangular Coordinates Conversion
The video begins with a recap of the previous lesson on converting between polar and rectangular coordinates. The host explains that while converting from polar to rectangular is straightforward, the reverse process has some nuances to consider. The importance of understanding the angle's quadrant and the use of trigonometric identities to convert between the two systems are emphasized.
📐 Identifying Coordinates and Plotting Points
The host instructs viewers to identify the x and y values of a point in rectangular coordinates and then plot the point to determine its quadrant. This step is crucial for converting to polar coordinates, as it informs the calculation of r and the correct angle θ. The process of finding r using the Pythagorean theorem and θ using the tangent inverse is detailed.
🔢 Dealing with Tangent Inverse and Quadrants
The video discusses the limitations of the tangent inverse function, which only provides angles from negative π/2 to π/2. This means it cannot directly give angles for points in quadrants two or three. The host explains how to adjust the angle by adding π to match the correct quadrant for these points. Additionally, for points in quadrant four, if a positive angle is required, 2π should be added instead of π.
🤔 Understanding Tangent's Behavior in Different Quadrants
The host delves into why the tangent function behaves as it does, not distinguishing between a negative y over a positive x and a positive y over a negative x, both resulting in a negative ratio. This is why the tangent inverse can only provide one quadrant's worth of angles at a time, necessitating the addition of π or 2π to find the correct angle for other quadrants.
📈 Converting Specific Points to Polar Coordinates
The host works through several examples of converting specific points from rectangular to polar coordinates. Each example illustrates the process of finding r and θ, with attention given to adjusting the angle based on the point's quadrant. The importance of plotting the point to determine the quadrant before calculating the angle is emphasized.
🧮 Handling Decimal Coordinates and Approximations
The video addresses the conversion of points with decimal coordinates to polar coordinates. The host demonstrates how to handle decimal values by approximating them and using a calculator to find the tangent inverse. The process remains the same, with the quadrant determining whether π or 2π needs to be added to the angle for an accurate conversion.
🔍 Final Examples and Recap
The host concludes with more examples, reinforcing the process of converting rectangular coordinates to polar coordinates. Emphasis is placed on the importance of understanding the relationship between the angle given by the tangent inverse and the point's quadrant. A reminder is given to add π for points in quadrants two and three, and 2π for points in quadrant four if a positive angle is needed.
Mindmap
Keywords
💡Polar Coordinates
💡Rectangular Coordinates
💡Tangent Inverse (Arctan or Tan^-1)
💡Pythagorean Theorem
💡Quadrants
💡Ambiguity
💡Sine and Cosine
💡Angle Addition
💡Conversion Process
💡Trigonometric Functions
💡Unit Circle
Highlights
The video explains how to convert between rectangular and polar coordinates, emphasizing the difference in representation and the mathematical formulas involved.
Polar coordinates are represented as (r, θ), where r is the radius and θ is the angle, offering a different perspective from the Cartesian (x, y) system.
The conversion from polar to rectangular uses the formulas x = r * cos(θ) and y = r * sin(θ), derived from the properties of a right triangle.
To convert from rectangular to polar, one can use the Pythagorean theorem to find r, and the arctangent function to find θ.
The arctangent function has a limitation, as it only spans from -π/2 to π/2, which can lead to ambiguity when determining the correct quadrant for the angle.
For points in quadrants II or III, the angle obtained from the arctangent function must be adjusted by adding π to align with the correct quadrant.
Points in quadrant IV may require adding 2π to the angle if a positive angle is necessary, despite the period of tangent being π.
The video provides a step-by-step guide on how to identify the quadrant of a point and apply the correct mathematical adjustments to find the polar coordinates.
The importance of plotting the point and understanding the relationship between x, y, and r is emphasized for accurate conversion.
The video demonstrates multiple examples, including points with decimals, to illustrate the process of conversion and the handling of different quadrant scenarios.
Approximations are used for ease of understanding, but the video also shows how to work with exact values for a precise conversion.
The presenter clarifies the rationale behind adding π or 2π to the angle based on the quadrant in which the point lies, avoiding confusion with the tangent function's limitations.
The video concludes with a note on future lessons, which will cover converting equations from rectangular to polar and vice versa, expanding on the concepts introduced.
Throughout the video, the presenter stresses the importance of understanding the mathematical reasoning behind the conversions, rather than just memorizing formulas.
The use of a calculator for finding the arctangent of complex numbers is demonstrated, showing how to work with non-integer values in polar coordinates.
The video provides a comprehensive understanding of polar coordinates, making it an excellent resource for students and those interested in coordinate geometry.
Transcripts
Browse More Related Video

Introduction to Polar Coordinates (Precalculus - Trigonometry 36)
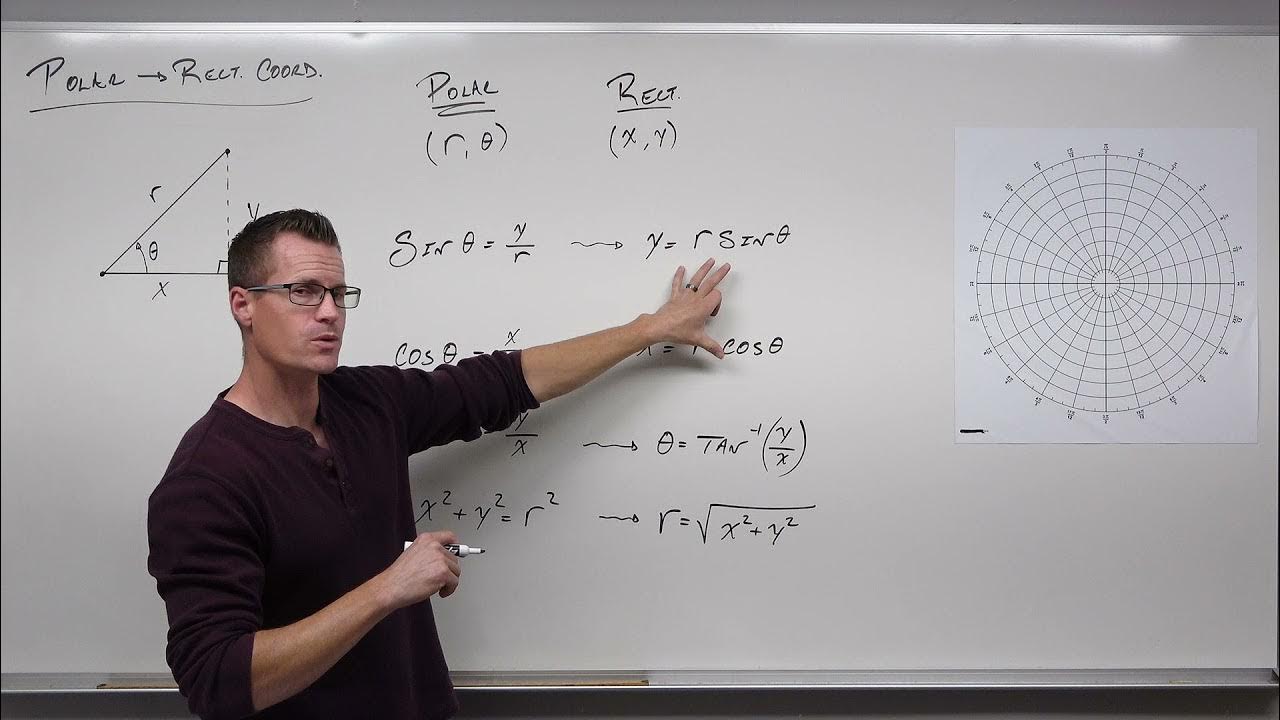
How to Convert From Polar Coordinates to Rectangular Coordinates (Precalculus - Trigonometry 37)

Polar coordinates 2 | Parametric equations and polar coordinates | Precalculus | Khan Academy

AP Precalculus Practice Exam Question 15
Polar Coordinates and Polar Graphs
Ch. 8.1 Polar Coordinates
5.0 / 5 (0 votes)
Thanks for rating: