13.3b Ex1 MJ20 P42 Q1 Rock Potential Energy | A2 Gravitational Fields | Cambridge A Level Physics

ETphysics

30 Jun 202126:56

EducationalLearning

32 Likes 10 Comments

TLDRThe video script discusses the concept of gravitational potential and its application to a rocket orbiting Earth. It delves into defining gravitational potential (phi) as work done per unit mass from infinity and illustrates how potential varies with distance from a solid sphere. The script then applies this knowledge to calculate the change in gravitational potential energy as a rock moves from 4r to 3r in a planet's gravitational field, emphasizing the conversion of potential energy to kinetic energy and the resulting increase in the rock's speed. The importance of negative potential in demonstrating gravity's attractive nature is highlighted.

Takeaways

📚 The definition of gravitational potential (phi) is the work done per unit mass to bring an object from infinity to a point in a gravitational field, with the potential at infinity considered zero.
📈 The gravitational potential varies inversely with the distance (r) from the center of a mass, following the equation phi = -GM/r, where G is the gravitational constant, M is the mass of the central body, and r is the distance from the center.
🚀 For a solid sphere (or a planet without an atmosphere), the gravitational potential energy (GPE) of an object is calculated using the formula GPE = -GMm/R, where m is the mass of the object and R is the distance from the center of the sphere/planet.
📉 When an object moves closer to a massive body (like a planet), its gravitational potential energy decreases, which is indicative of the attractive nature of gravity.
🌐 The change in gravitational potential energy is determined by the difference in potential energy between two points, calculated as ΔGPE = GPE(final) - GPE(initial).
🔄 The decrease in gravitational potential energy of an object approaching a planet is converted into an increase in kinetic energy, resulting in a faster speed.
🎨 When sketching graphs for gravitational potential and potential energy, it is crucial to accurately represent the negative values, the inverse relationship with distance, and the smooth curve progression.
📝 In exam scenarios, marks are often allocated for the correct application of formulas, accurate substitutions and calculations, and the correct explanation of physical concepts.
🕒 Time management is key during exams; aim to spend approximately one minute per mark on a question, focusing on understanding the question and then addressing each part efficiently.
📊 Sketching graphs can be worth a significant portion of the marks; ensure the graph accurately reflects the physical situation, including important values, the shape of the curve, and the correct polarity (positive/negative).
🌍 Understanding the relationship between gravitational potential, gravitational potential energy, and an object's distance from a central mass is essential for solving problems related to gravitational interactions.

Q & A

What is the definition of gravitational potential?
-Gravitational potential, denoted as phi, is the work done per unit mass in bringing an object from infinity to a point in a gravitational field. It is a measure of the potential energy at a point in the field due to gravity.
Why is gravitational potential considered to start from infinity?
-Gravitational potential is considered to start from infinity because by definition, the potential at infinity is zero. This provides a reference point from which to measure changes in potential energy as an object moves within a gravitational field.
How does the gravitational potential vary with distance from the center of a solid sphere?
-The gravitational potential varies inversely with the distance from the center of a solid sphere. As the distance (d) from the center increases, the potential decreases, following the equation phi = -GM/d, where G is the gravitational constant, M is the mass of the sphere, and d is the distance from the center.
What is the relationship between gravitational potential and the radius of a planet?
-The gravitational potential at a point on the surface of a planet is inversely proportional to the radius of the planet. As the radius increases, the potential at the surface decreases, following the same equation phi = -GM/r, where r is the distance from the center (which, at the surface, is equal to the radius).
How does the gravitational potential energy (GPE) of a rock change as it moves from a greater distance to a lesser distance from a planet's center?
-As a rock moves from a greater distance (4r) to a lesser distance (3r) from a planet's center, its gravitational potential energy decreases. This is because GPE is given by the formula GPE = -GMm/r, where M is the mass of the planet, m is the mass of the rock, and r is the distance from the center of the planet. When r decreases, the value of 1/r increases, leading to a more negative (lower) GPE.
What is the significance of the negative value of gravitational potential?
-The negative value of gravitational potential signifies that the gravitational force is attractive. It indicates that work is done against the gravitational field when an object is moved from infinity to a point within the field, and this work is stored as potential energy.
How does the change in gravitational potential energy of a rock relate to its kinetic energy as it approaches a planet?
-As a rock loses gravitational potential energy while approaching a planet, this energy is converted into kinetic energy. Since there is no atmosphere to cause energy loss through friction, the increase in kinetic energy results in an increase in the rock's speed.
What is the equation for gravitational potential in the context of a planet with mass M and radius r?
-The equation for gravitational potential at a distance r from the center of a planet with mass M and radius r is given by phi = -GM/r, where G is the gravitational constant.
How does the gravitational potential energy (GPE) equation relate to the conservation of energy?
-The GPE equation is consistent with the conservation of energy principle. When a rock moves closer to a planet and loses GPE, this energy is not lost but rather converted into kinetic energy. The total mechanical energy (potential plus kinetic) remains constant, assuming no external forces like air resistance or friction.
What is the expected outcome when a rock with mass m approaches a planet with mass M from a distance of 4r to 3r?
-When a rock with mass m approaches a planet with mass M from a distance of 4r to 3r, the change in gravitational potential energy (ΔGPE) is calculated as ΔGPE = -GMm/3r + GMm/4r. This results in a decrease in GPE, indicating that the rock gains kinetic energy and its speed increases as it moves closer to the planet.
How can one determine the change in gravitational potential energy without a graph?
-The change in gravitational potential energy can be determined by using the GPE equation and calculating the difference in potential energy between two points. The change in potential energy (ΔGPE) is the final potential energy minus the initial potential energy, which, using the equation ΔGPE = -GMm/3r + GMm/4r, can be solved by substituting the known values and performing the calculation.

Outlines

00:00

🌌 Gravitational Potential and Rocket's Energy Change

This paragraph introduces the concept of gravitational potential and its relevance to the change in potential energy of a rocket orbiting the Earth. It emphasizes the definition of gravitational potential (phi) as the work done per unit mass to bring an object from infinity to a point in a gravitational field, with the convention that potential at infinity is zero. The discussion then shifts to a specific problem involving a solid sphere with mass m concentrated at its center, and the variation of gravitational potential with distance from the center of the sphere.

05:02

📉 Negative Gravitational Potential and Its Proportionality

The paragraph delves into the negative nature of gravitational potential, explaining that it is inversely proportional to the radius (r). This is demonstrated through a step-by-step analysis of how the potential changes as the distance (d) from the center of a sphere varies. The summary highlights the importance of understanding the relationship between gravitational potential and radius, and how this relationship can be visually represented in a graph, with the potential becoming more negative as the distance decreases.

10:04

🚀 Calculating Change in Gravitational Potential Energy

This section focuses on the calculation of the change in gravitational potential energy as a rock moves from a distance of 4r to 3r from the center of a planet. It explains the formula for gravitational potential energy and how to apply it to find the change in energy. The explanation includes the consideration of the mass of the planet and the rock, and the significance of the negative sign in the equation, indicating a decrease in potential energy as the rock moves closer to the planet.

15:06

🌍 Impact of Gravitational Potential Energy on Rock's Speed

The paragraph discusses the implications of the change in gravitational potential energy on the kinetic energy and, consequently, the speed of a rock approaching a planet. It clarifies that with no atmosphere to cause energy loss through friction, the loss of gravitational potential energy is fully converted into kinetic energy. The summary explains the calculation process and the resulting decrease in potential energy, leading to an increase in the rock's speed as it gets closer to the planet.

20:07

📈 Visualizing Gravitational Potential and Energy Change

This part of the script provides guidance on sketching the graph of gravitational potential and potential energy change against distance. It underscores the importance of accurately representing the negative gravitational potential and its inverse proportionality to the radius. The summary also touches on the expected decrease in gravitational potential energy and the corresponding increase in kinetic energy, as well as the significance of the graph's shape and the placement of key points to earn marks in an exam setting.

Mindmap

Keywords

💡Gravitational Potential

Gravitational potential, denoted by phi, is the work done per unit mass to move an object from infinity to a point within a gravitational field. In the context of the video, it is a key concept used to understand the change in potential energy of a rocket orbiting the Earth. The video explains that gravitational potential is inversely proportional to the distance from the center of a gravitational source, such as a planet, and is always negative, reflecting the attractive nature of gravity.

💡Potential Energy

Potential energy is the energy an object possesses due to its position in a force field, such as gravity. In the video, the change in gravitational potential energy (GPE) of a rock falling towards a planet is calculated. The GPE is related to the work done against gravity and is given by the formula -G * (mass of the planet * mass of the object) / r, where G is the gravitational constant, and r is the distance from the center of the planet. As the rock moves closer to the planet, its GPE decreases, indicating a loss of potential energy which is converted into kinetic energy.

💡Rocket Orbit

A rocket orbit refers to the path followed by a rocket as it revolves around a celestial body, such as the Earth, due to the gravitational pull of that body. The video discusses the concept of gravitational potential and potential energy in the context of a rocket orbiting the Earth. The orbit is influenced by the gravitational forces and the energy exchanges that occur as the rocket moves through different points in its path.

💡Work Done

In physics, work done refers to the transfer of energy that occurs when a force causes an object to move through a distance. The video emphasizes that gravitational potential is related to the work done per unit mass to move an object from infinity to a specific point in a gravitational field. The concept is crucial for understanding how much energy is required to move an object against the gravitational pull of a planet or other celestial bodies.

💡Law of Universal Gravitation

The Law of Universal Gravitation, also known as Newton's law of gravitation, states that every point mass attracts every other point mass by a force acting along the line intersecting both points. The force is proportional to the product of the two masses and inversely proportional to the square of the distance between them. In the video, this law is fundamental to understanding gravitational potential and potential energy, as it describes the gravitational force that acts on objects in space and influences their orbits around Earth.

💡Infinite Distance

In the context of gravitational potential, infinite distance refers to a reference point outside the influence of a gravitational field, where the potential is defined as zero. This concept is used to establish a baseline from which changes in potential can be measured. The video explains that all measurements of gravitational potential are made starting from this point of zero potential at infinity.

💡Solid Sphere

A solid sphere in the context of the video is an idealized geometrical object used to illustrate the concept of gravitational potential. It is assumed to have all its mass concentrated at its center, which simplifies the calculations of gravitational forces and potentials. The video uses the example of a solid sphere to show how gravitational potential varies with the distance from the center of the sphere.

💡Graph Sketching

Graph sketching is the process of visually representing data or relationships between variables through a graph. In the video, it is an essential skill for illustrating the variation of gravitational potential with distance and for understanding the changes in potential energy. The video emphasizes the importance of accurately plotting points and connecting them with a smooth curve to reflect the correct relationship between variables.

💡Kinetic Energy

Kinetic energy is the energy an object possesses due to its motion. In the video, it is explained that as a rock falls towards a planet and loses gravitational potential energy, this energy is converted into kinetic energy. The increase in kinetic energy implies an increase in the speed of the rock as it gets closer to the planet.

💡Energy Conservation

Energy conservation is the principle that the total amount of energy in an isolated system remains constant, though it may change from one form to another. In the video, this principle is applied to explain that the loss of gravitational potential energy by a rock falling towards a planet is converted into kinetic energy, without any loss to friction or air resistance due to the absence of an atmosphere.

💡Mark Scheme

A mark scheme is a set of guidelines used to award marks for answers in an examination. It outlines the criteria that need to be met for each mark to be awarded. In the video, the mark scheme is referenced to explain how students can structure their answers to maximize the number of marks obtained, particularly in the context of sketching graphs and explaining concepts related to gravitational potential and potential energy.

Highlights

Definition of gravitational potential as work done per unit mass from infinity to a point in a gravitational field, with gravitational potential at infinity being zero.

Gravitational potential is inversely proportional to the radius, indicating its negative nature due to the attractive property of gravity.

The variation of gravitational potential with distance from the center of a solid sphere is discussed, highlighting the relationship between potential and radius.

The importance of visual representation in understanding gravitational potential, with the suggestion to draw a sphere for context.

The equation for gravitational potential is derived as negative GM/r, where G is the gravitational constant, M is the mass of the celestial body, and r is the distance from the center.

The potential at the surface of a sphere is given as negative, emphasizing the fundamental property of gravitation being attractive.

A detailed explanation of how the gravitational potential changes with varying radius values (r, 2r, 3r, 4r), and the corresponding potential values.

The significance of plotting the gravitational potential graph for theory papers, with marks allocated for the shape, important values, and the negative polarity of the potential.

The calculation of the change in gravitational potential energy as a rock moves from a distance of 4r to 3r from the center of a planet, using the derived equation.

The explanation of the conversion of gravitational potential energy into kinetic energy as a rock approaches a planet without atmospheric friction.

The expectation of a decrease in gravitational potential energy and the corresponding increase in kinetic energy, indicating an increase in the rock's speed.

The application of the gravitational potential energy equation and the correct substitution of values to calculate the change in potential energy.

The marking scheme for the question is explained, emphasizing the independent nature of the marks and the importance of each step in the calculation and explanation process.

The practical application of the concepts discussed, such as the impact of gravitational potential and kinetic energy on a rock approaching a planet's surface.

The importance of understanding the negative nature of gravitational potential and its implications for the attractive property of gravity.

The comprehensive approach to explaining the relationship between gravitational potential, potential energy, and kinetic energy, providing a clear understanding of the concepts.

Transcripts

Browse More Related Video

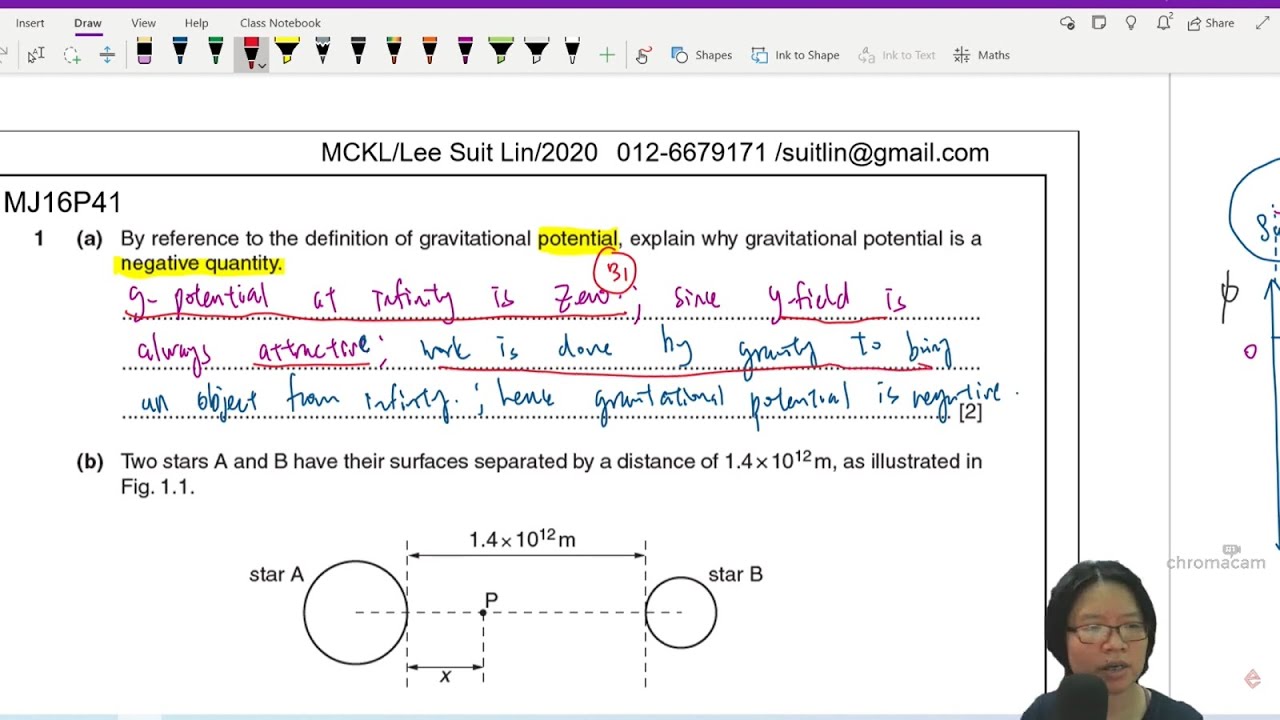
MJ16 P41 Q1 Gravitational Potential Between 2 Stars | A2 G-fields | Cambridge A Level 9702 Physics

13.3a Gravitational Potential Theory | A2 G-Fields | Cambridge A Level Physics

Gravitational Potential Questions | A Level Physics | Formulas, Key Words, Graphs

Gravitational Potential and Gravitational Potential Energy

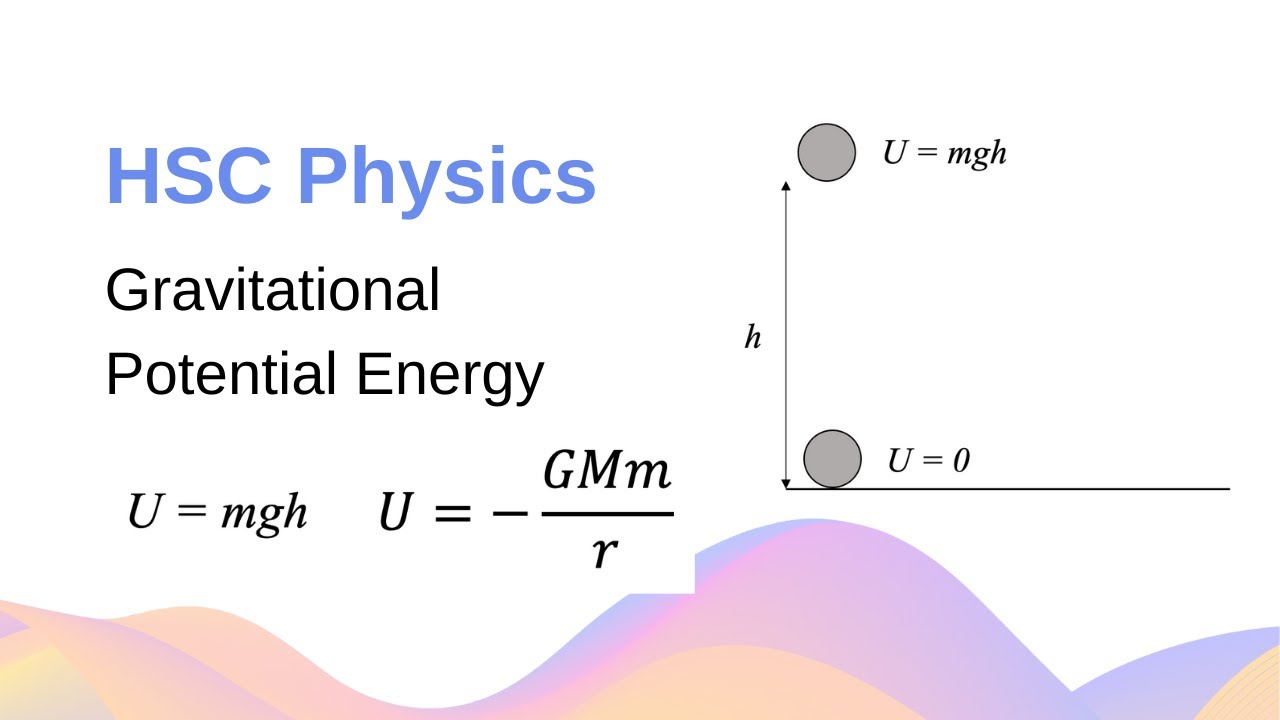
Gravitational Potential Energy & Work Done + Calculation Example // HSC Physics

Gravitational potential energy at large distances | AP Physics 1 | Khan Academy

Related Tags

GravitationalPotential PotentialEnergy RocketOrbit PhysicsConcepts CelestialMechanics EnergyConversion SpaceExploration AstrophysicalProcesses EducationalContent TechnicalExplanation