Gravitational potential energy at large distances | AP Physics 1 | Khan Academy

Khan Academy
30 Mar 201805:04
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video delves into the concept of gravitational potential energy, emphasizing its relationship with an object's mass, position, and the Earth's gravitational field. It introduces a more precise formula for calculating gravitational potential energy, considering the non-constant nature of the gravitational field. The video also discusses Newton's Law of Gravity, highlighting how the potential energy becomes less negative with increasing distance and approaches zero as distance goes to infinity, providing a comprehensive understanding of the concept.

Takeaways
  • πŸ“š The concept of gravitational potential energy is reviewed, focusing on its calculation when an object's position changes in the vertical direction on Earth.
  • 🌍 The gravitational field (G) is assumed constant near the Earth's surface for simplicity, but it can vary with distance from the object generating the field.
  • πŸ”„ Newton's Law of Gravity is introduced to derive a more precise formula for gravitational potential energy, considering the masses of two objects and the distance between their centers of mass.
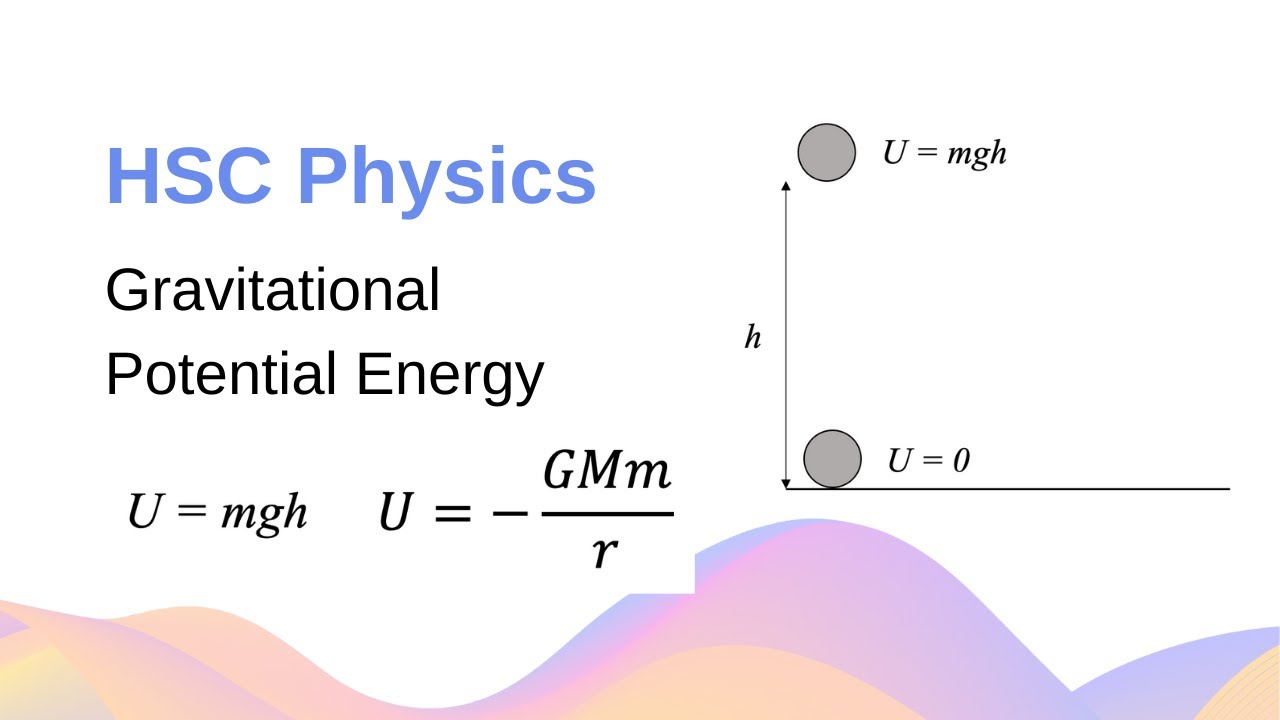
  • πŸ“ˆ The gravitational potential energy (PE) is given by the formula PE = -G * (M1 * M2) / r, where M1 is the mass of the object experiencing the force, M2 is the mass generating the field, and r is the distance between the centers of mass.
  • 🌐 The potential energy is negative and becomes less negative with increasing distance, approaching zero as r goes to infinity, reflecting the balance between the gravitational force and the object's position.
  • πŸ”§ The script suggests a practical approach to understanding gravitational potential energy by combining the principles of Newton's Law of Gravity with the concept of potential energy.
  • πŸ“Š The change in gravitational potential energy (Ξ”PE) is calculated as the product of the mass of the object (M), the gravitational field (G), and the change in vertical position (Ξ”y).
  • 🌟 The script emphasizes the importance of understanding the relationship between the gravitational field, the masses involved, and the distance between them to accurately calculate gravitational potential energy.
  • πŸ”„ The potential energy is related to the work done against gravity when an object is raised or lowered, which is a key concept in classical mechanics.
  • πŸ“š The script sets the stage for future discussions on applying the concept of gravitational potential energy to solve more complex problems.
Q & A

  • What is the concept of gravitational potential energy discussed in the script?

    -Gravitational potential energy is the energy an object possesses due to its position in a gravitational field, specifically in the vertical direction on Earth.

  • How is the change in gravitational potential energy calculated?

    -The change in gravitational potential energy is calculated by multiplying the mass of the object (M), the gravitational field (G), and the change in vertical position (delta y).

  • What is the assumption made regarding the gravitational field when calculating potential energy?

    -The assumption made is that the gravitational field (G) is constant, which is reasonable when near the surface of a planet and for relative calculations.

  • What does Newton's Law of Gravity state?

    -Newton's Law of Gravity states that the force between two objects is equal to the gravitational constant (G) times the product of their masses (M1 and M2) divided by the square of the distance (r) between their centers of mass.

  • How does the gravitational field strength vary with distance?

    -The gravitational field strength is inversely proportional to the square of the distance (r) from the object generating the field, meaning it decreases as the distance increases.

  • What is the absolute formula for gravitational potential energy?

    -The absolute formula for gravitational potential energy is given by the mass of the object (M1) times the gravitational field strength (G * M2 / r^2) times the height above the center of mass of the object generating the field.

  • Why is the potential energy considered negative in the absolute formula?

    -The potential energy is considered negative to account for the fact that as distance (r) increases, the potential energy becomes less negative, and at infinity, it approaches zero.

  • What happens to gravitational potential energy as the distance from the gravitational source increases?

    -As the distance from the gravitational source increases, the gravitational potential energy becomes less negative, indicating an increase in potential energy.

  • At what point does gravitational potential energy approach zero?

    -Gravitational potential energy approaches zero as the distance (r) becomes infinitely large, or as the object moves far away from the gravitational field source.

  • How does the script relate the concept of gravitational potential energy to Newton's Law of Gravity?

    -The script shows that the formula for gravitational potential energy is derived from Newton's Law of Gravity, with a negative sign in front and dividing by r instead of r squared.

  • What is the significance of the absolute formula for gravitational potential energy?

    -The absolute formula for gravitational potential energy provides a precise and universal way to calculate potential energy, regardless of the object's position, and aligns with the idea that potential energy increases with distance from the gravitational source.

Outlines
00:00
πŸ“š Gravitational Potential Energy Review and Precision

This paragraph begins with a review of the concept of gravitational potential energy, emphasizing the need for precision in understanding its calculation. The tutor introduces the scenario of an object with mass M being moved vertically in Earth's gravitational field, represented by G. The change in gravitational potential energy is described as the product of the object's mass, the gravitational field, and the change in vertical position (delta y). The discussion then delves into the assumption of a constant gravitational field, questioning whether there's a way to determine an absolute value for gravitational potential energy. The tutor revisits Newton's Law of Gravity to explore how the gravitational field is not constant but varies with the distance between two masses (r). This leads to the derivation of an absolute formula for gravitational potential energy, highlighting that it is negative and becomes less negative with increasing distance, approaching zero as r goes to infinity.

Mindmap
Keywords
πŸ’‘potential energy
Potential energy is the stored energy an object possesses due to its position relative to other objects, forces, or fields. In the context of this video, gravitational potential energy is the focus, which is the energy an object has because of its position in a gravitational field. The video explains how changing an object's position vertically on Earth's surface affects its gravitational potential energy.
πŸ’‘gravitational potential energy
Gravitational potential energy is a specific type of potential energy associated with the position of an object within a gravitational field, such as Earth's. It is directly related to the object's mass, the gravitational field strength, and its height above a reference point. The video delves into the concept by discussing how the change in height results in a change in gravitational potential energy, denoted as Ξ”U = Mgy, where M is the mass, g is the acceleration due to gravity, and y is the height change.
πŸ’‘gravitational field
The gravitational field is a region in space where a gravitational force is exerted. It is produced by masses, such as planets, and affects objects within its influence. In the video, the Earth's gravitational field is assumed to be constant for simplicity, but the tutor also explores the concept of varying gravitational fields with distance, leading to a more precise formula for gravitational potential energy.
πŸ’‘Newton's Law of Gravity
Newton's Law of Gravity states that every point mass attracts every other point mass by a force acting along the line intersecting both points. The force is proportional to the product of the two masses and inversely proportional to the square of the distance between them. This law is fundamental in understanding how the gravitational potential energy is related to the masses and the distance between them, as discussed in the video.
πŸ’‘mass
Mass is a measure of the amount of matter in an object, and it is a fundamental property that determines the strength of the gravitational force acting on the object. In the video, the mass of the object (M) is a key factor in calculating its gravitational potential energy. The greater the mass, the greater the gravitational force and, consequently, the greater the potential energy at a given height.
πŸ’‘vertical direction
The vertical direction refers to the direction perpendicular to the Earth's surface. In the context of the video, it is the axis along which the object's position is changed to illustrate the concept of gravitational potential energy. The change in the vertical position (delta y) of the object results in a change in its gravitational potential energy.
πŸ’‘change in potential energy
Change in potential energy refers to the difference in potential energy before and after a change in the position of an object within a force field. In the video, this concept is used to explain how the gravitational potential energy of an object changes when its position in the Earth's gravitational field is altered. The formula Ξ”U = Mgy is used to calculate this change, where M is the mass, g is the gravitational field strength, and y is the change in height.
πŸ’‘absolute formula
An absolute formula is a mathematical expression that provides a precise and universally applicable relationship between variables. In the video, the tutor derives an absolute formula for gravitational potential energy by considering the non-constant nature of the gravitational field and applying Newton's Law of Gravity. This formula allows for the calculation of gravitational potential energy at any point in space, not just near the Earth's surface.
πŸ’‘negative potential energy
Negative potential energy refers to the convention used in physics where potential energy in a gravitational field is considered negative because it represents the energy an object has due to being lifted against the gravitational force. In the video, the tutor explains that gravitational potential energies are always negative, becoming less negative as one moves further away from the source of the gravitational field, and approaching zero as the distance goes to infinity.
πŸ’‘center of mass
The center of mass is the point at which the mass of an object, or a system of objects, is concentrated for the purposes of understanding its motion. It is the balance point of the system. In the video, the concept is used to discuss the height above the center of mass of the Earth when calculating the gravitational potential energy, which is a crucial factor in the derived absolute formula for potential energy.
πŸ’‘infinite distance
Infinite distance refers to a theoretical point that is infinitely far away from a reference point. In the context of the video, it is used to discuss the behavior of gravitational potential energy as the distance from the Earth (or any massive object) becomes extremely large. The video explains that as the distance approaches infinity, the gravitational field strength approaches zero, and consequently, the potential energy also approaches zero.
Highlights

Review of potential energy with a focus on gravitational potential energy.

An object with mass M changes position vertically in Earth's gravitational field G.

The change in gravitational potential energy is given by the mass times the gravitational field times the change in vertical position (delta y).

Assumption of a constant gravitational field is suitable for calculations near the Earth's surface and on a relative basis.

Absolute calculation of gravitational potential energy requires revisiting Newton's Law of Gravity.

Newton's Law of Gravity states that the force between two masses (M1 and M2) is proportional to the product of their masses and inversely proportional to the square of the distance between their centers of mass (r).

Gravitational field strength varies with distance, being given by the gravitational constant times the mass of the object generating the field divided by r squared.

The absolute formula for gravitational potential energy is derived by considering the mass of the object in the field (M1), the mass of the field-generating object (M2), and the height above the field-generating object's center of mass.

The potential energy at the center of mass of the field-generating object is considered zero for the sake of calculation.

As distance (r) from the field-generating object's center of mass increases, the gravitational potential energy becomes less negative, approaching zero at infinity.

The gravitational potential energy formula is represented as negative the gravitational constant times the product of the two masses divided by the distance (r).

The formula for gravitational potential energy aligns with the concept that potential energy increases with distance from the source, becoming less negative.

At infinity, the gravitational field and potential energy both approach zero.

The absolute formula for gravitational potential energy provides a comprehensive understanding and meets the necessary properties for all scenarios.

The application of the absolute gravitational potential energy formula will be explored in future videos.

Transcripts

Browse More Related Video

What is Gravitational Potential Energy - a deeper understanding

AP Physics 1: Universal Gravitation Review

Potential energy and gravity

Gravitational Potential Energy & Work Done + Calculation Example // HSC Physics

Gravitational Potential and Gravitational Potential Energy

Gravitational Potential Questions | A Level Physics | Formulas, Key Words, Graphs

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Physics ConceptsGravitational EnergyNewton's LawGravitational FieldPotential EnergyAbsolute FormulaEarth's CenterInfinite DistanceEducational ContentScientific Exploration