What is Gravitational Potential Energy - a deeper understanding
TLDRIn the video, the presenter delves into the concept of gravitational potential energy using a teddy bear as a relatable example. The discussion covers the relationship between an object's position in a gravitational field and its energy, emphasizing that gravitational potential energy is relative and depends on changes in position. The video also clarifies the difference between gravitational potential energy and work done in a gravitational field, and introduces the formula for calculating gravitational potential energy, highlighting its dependence on the distance from the gravitational source and the limitations of the classical mgh formula. The use of graphical analysis and calculus to understand the work done by the gravitational field is also explored, ultimately providing a deeper comprehension of how gravitational potential energy influences an object's movement within a gravitational field.
Takeaways
- 🌐 Gravitational potential energy increases with the height of an object lifted in a gravitational field.
- 📈 The change in gravitational potential energy is related to the work done against or by the gravitational field.
- 🎈 Gravitational energy and gravitational potential energy are often used interchangeably, but the latter emphasizes position in a gravitational field.
- 🔨 Work is done on an object when its gravitational energy changes, either by lifting or dropping it.
- 🚀 The conservation of energy principle states that the total energy remains constant, shifting between potential and kinetic forms.
- 📉 As an object with mass moves towards a gravitational field, gravitational energy decreases and kinetic energy increases.
- 📱 The mgh formula for gravitational potential energy is limited and assumes constant gravitational field strength.
- 🌌 Gravitational field strength varies with distance according to Newton's law of universal gravitation (g m m / r squared).
- 📊 Graphical analysis and calculus can be used to find the area under the force-displacement graph, representing work done.
- 🌠 The change in gravitational energy is given by the formula U = -G * (m1 * m2) / r, where U is negative and increases as distance (r) decreases.
- 🚀 Understanding gravitational energy is essential for calculating escape velocity and other space-related phenomena.
Q & A
What is gravitational potential energy?
-Gravitational potential energy is the energy an object possesses due to its position in a gravitational field, typically related to its height above the ground or another reference point.
How does lifting an object affect its gravitational potential energy?
-Lifting an object increases its gravitational potential energy because it is being raised to a higher position in the gravitational field, thus increasing the potential energy due to gravity.
What happens to the gravitational potential energy when an object is dropped?
-When an object is dropped, its gravitational potential energy decreases as it falls and its position in the gravitational field lowers.
What is the relationship between gravitational potential energy and an object's position in a gravitational field?
-The gravitational potential energy of an object is directly related to its position in a gravitational field. The higher the object is lifted, the greater its gravitational potential energy. Conversely, the lower the object is, the less gravitational potential energy it has.
How does the concept of work relate to gravitational potential energy?
-Work is done on an object when it is lifted or dropped, changing its displacement in a gravitational field. This work is equivalent to the change in gravitational potential energy of the object.
What is the formula for calculating gravitational potential energy?
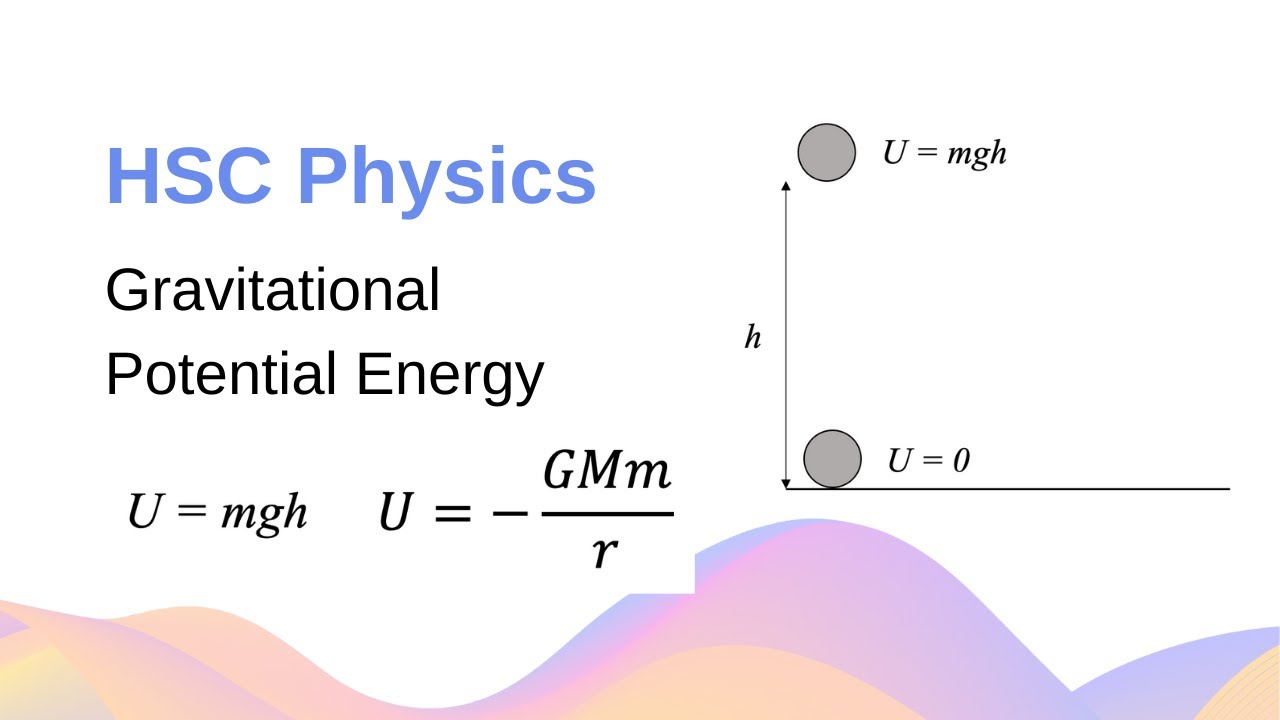
-The formula for calculating gravitational potential energy is U = mgh, where U is the gravitational potential energy, m is the mass of the object, g is the acceleration due to gravity, and h is the height of the object above the reference point.
Why is the mgh formula for gravitational potential energy considered limited?
-The mgh formula is considered limited because it assumes that the gravitational acceleration (g) is constant, which is not the case. The actual gravitational field strength varies depending on the distance from the objects involved, following Newton's law of universal gravitation, which states that the force between two masses is proportional to the product of their masses and inversely proportional to the square of the distance between them.
How does the concept of work relate to changes in gravitational potential energy?
-Work is related to changes in gravitational potential energy in that work done on an object by lifting it (applying an upward force) increases its gravitational potential energy, while work done by the gravitational field on a falling object (the object being accelerated by gravity) decreases its gravitational potential energy.
What is the significance of the conservation of energy principle in the context of gravitational potential energy?
-The conservation of energy principle states that the total energy in an isolated system remains constant. In the context of gravitational potential energy, when an object falls and loses gravitational potential energy, it gains an equivalent amount of kinetic energy, maintaining the total energy of the system.
How does the gravitational field strength vary with distance according to Newton's law of universal gravitation?
-According to Newton's law of universal gravitation, the gravitational field strength varies with the square of the distance between two objects. The force between two masses is directly proportional to the product of their masses and inversely proportional to the square of the distance between them. This means that as the distance increases, the gravitational field strength decreases, and vice versa.
What is the alternative formula for gravitational potential energy that accounts for the varying gravitational field strength?
-The alternative formula for gravitational potential energy that accounts for the varying gravitational field strength is U = -GMm/r, where U is the gravitational potential energy, G is the gravitational constant, M and m are the masses of the two objects involved, and r is the distance between the centers of the two masses.
Outlines
🌟 Introduction to Gravitational Potential Energy
The video begins with an introduction to gravitational potential energy, explaining how it is related to the height an object is lifted. The speaker uses a teddy bear as a demonstrative tool, drawing parallels to a previous video that utilized a cartoon image. The aim is to provide a deeper understanding of gravitational potential energy, clarifying that the energy is about the object's position in a gravitational field rather than being stored within the object. The speaker also reviews key concepts such as the interchangeability of 'gravitational energy' and 'gravitational potential energy,' and the importance of understanding work in relation to changes in gravitational energy.
📚 Gravitational Energy and the mgh Formula
This paragraph delves into the limitations of the mgh formula, which is often used to calculate changes in gravitational potential energy. The speaker explains that the gravitational field strength is not constant and varies with distance, making the mgh formula less accurate for large-scale scenarios. The concept of work is further explored, with the speaker emphasizing that work is done on an object when its displacement changes due to an applied force. The speaker introduces a graphical analysis to illustrate how the work done is represented by the area under the force-displacement graph, leading to a new formula for calculating changes in gravitational energy that accounts for the inverse square law of Newton's gravitational law.
📈 Understanding Gravitational Energy through Graphs
The speaker introduces the concept of using graphs to understand gravitational energy. By graphing force against displacement, the area under the curve represents the work done, which is equivalent to the change in gravitational potential energy. The speaker explains that calculus, specifically integration, is used to calculate this area. The new formula derived from the graphical analysis is U = -G * (m1 * m2) / r, where G is the gravitational constant, m1 and m2 are the masses of the objects, and r is the distance between their centers. The speaker emphasizes that the negative sign indicates the direction of the energy change and that the gravitational energy is considered zero at infinity for simplicity.
🚀 Gravitational Energy in Earth's Field and Escape Velocity
In the final paragraph, the speaker discusses how the concept of gravitational energy can be applied to understand the escape velocity, which is the minimum speed required for an object to break free from a gravitational field. The speaker clarifies the graphical representation of gravitational energy as a negative value that increases when moving away from the Earth, indicating an increase in energy. The speaker concludes by encouraging viewers to like, share, and subscribe for more content on similar topics, and signs off with a promise to cover escape velocity in a future video.
Mindmap
Keywords
💡Gravitational Potential Energy
💡Conservation of Energy
💡Work
💡Displacement
💡Gravitational Field
💡Newton's Law of Universal Gravitation
💡Inverse Square Law
💡Calculus
💡Escape Velocity
💡Relative
💡Kinetic Energy
Highlights
The bowling ball has gravitational potential energy that increases with height.
The video uses a teddy bear to demonstrate the concept of gravitational potential energy.
Gravitational energy and gravitational potential energy are often used interchangeably, but the latter relates to an object's position in a gravitational field.
Changing an object's gravitational energy involves doing work on it, whether lifting it up or allowing it to fall.
The change in gravitational energy is represented by the formula u = mgh, where u is the change in energy, m is mass, g is gravitational acceleration, and h is height.
The conservation of energy principle states that as an object falls and gains kinetic energy, it loses gravitational potential energy.
Gravitational energy is relative and not necessarily zero when an object is not moving; it depends on the object's position in the gravitational field.
The mgh formula is limited because it assumes a constant gravitational field strength, which is not the case in larger scales.
The gravitational field strength varies with distance and is determined by Newton's law of gravitation, which is an inverse square relationship.
A better model for gravitational energy change involves the formula u = -GMm/r, where G is the gravitational constant, M and m are masses, and r is the distance between centers of the two masses.
Work done is represented by the area under the force-displacement graph, which is integral to understanding changes in gravitational energy.
Calculus, specifically integration, is used to determine the area under the graph and thus the work done or change in gravitational energy.
The gravitational energy is negative because the starting point of zero gravitational energy is defined at infinity, where the gravitational field strength is effectively zero.
As an object moves closer to the Earth within a gravitational field, its gravitational energy decreases, and it gains kinetic energy.
The concept of gravitational energy can be applied to calculate escape velocity, which is the speed needed for an object to break free from a gravitational field.
The video aims to provide a deeper understanding of gravitational potential energy using a relatable and visual approach.
The demonstration with the teddy bear is intended to build upon a previous video that used a cartoon image for similar educational purposes.
Transcripts
Browse More Related Video

Gravitational Potential and Gravitational Potential Energy

Gravitational potential energy at large distances | AP Physics 1 | Khan Academy

Gravitational Potential Questions | A Level Physics | Formulas, Key Words, Graphs

Potential energy and gravity
Gravitational Potential Energy & Work Done + Calculation Example // HSC Physics

GCSE Physics - Gravity, Weight and GPE #3
5.0 / 5 (0 votes)
Thanks for rating: