Inverting 3x3 part 1: Calculating matrix of minors and cofactor matrix | Precalculus | Khan Academy
TLDRThe video script outlines the process of manually inverting a 3x3 matrix, a tedious task that is better suited for computational methods. The speaker guides the audience through constructing a matrix of minors, calculating determinants, and applying a checkerboard pattern to obtain the cofactor matrix. The final step involves using the determinant to find the inverse of the matrix, emphasizing the complexity and potential for error in manual computation.
Takeaways
- 🧠 Inverting a 3x3 matrix is a complex and computationally-intensive task that is better performed by a computer.
- 🤔 The process begins by constructing a matrix of minors, which involves creating a new matrix and replacing each element with the determinant of the remaining elements after crossing out its row and column.
- 🔢 To find the minor of an element, remove the row and column corresponding to that element and calculate the determinant of the remaining submatrix.
- 🎨 The script provides a step-by-step example of calculating the minors for a given 3x3 matrix, emphasizing the potential for human error and the time-consuming nature of the process.
- 🔄 After obtaining the matrix of minors, the next step is to create the cofactor matrix by applying a checkerboard pattern of positive and negative signs to the minors.
- 🔢 The determinant of each minor is calculated by following standard rules for finding the determinant of a 2x2 matrix.
- 💠 The cofactor matrix is derived from the matrix of minors by alternating signs in a pattern resembling a checkerboard.
- 📈 The final step to find the inverse of a matrix is to use the cofactor matrix and the determinant of the original matrix.
- 🌟 The inverse of a matrix is obtained by multiplying each element of the cofactor matrix by 1 over the determinant of the original matrix.
- 📚 The script serves as an educational example of the matrix inversion process, highlighting the importance of precision and patience.
- 🚫 Matrix inversion of larger matrices, such as 4x4 or 5x5, is even more challenging and time-consuming, potentially leading to more errors if done manually.
Q & A
What is the main task being discussed in the transcript?
-The main task discussed in the transcript is inverting a 3x3 matrix manually, which is a computationally-intensive process.
Why is inverting a matrix considered better done by a computer?
-Inverting a matrix is considered better done by a computer because it is a complex and error-prone process when done manually, especially for larger matrices, which can take a long time and increase the likelihood of making careless mistakes.
What is the first step in inverting a 3x3 matrix as described in the transcript?
-The first step in inverting a 3x3 matrix, as described in the transcript, is to construct a matrix of minors by replacing each element with the determinant of the elements that remain after crossing out the corresponding row and column.
How is the matrix of minors related to the original matrix?
-The matrix of minors is directly related to the original matrix as it is constructed by finding the determinants of the submatrices formed by removing each element's corresponding row and column from the original matrix.
What is the significance of the checkerboard pattern in the cofactor matrix?
-The checkerboard pattern in the cofactor matrix is significant because it represents the alternating signs that are applied to the elements of the matrix of minors to obtain the cofactors. This pattern helps in remembering and applying the correct signs to each cofactor.
How does one obtain the cofactor matrix from the matrix of minors?
-To obtain the cofactor matrix from the matrix of minors, one applies a checkerboard pattern of positive and negative signs to each element of the matrix of minors, starting with a positive sign at the top left and alternating thereafter.
What is the final step in finding the inverse of a matrix?
-The final step in finding the inverse of a matrix is to multiply the cofactor matrix by the reciprocal of the original matrix's determinant.
Why might one want to invert a matrix?
-One might want to invert a matrix to solve systems of linear equations, as the inverse of a matrix can be used to find the solution to such systems when the matrix is square and non-singular.
What is the determinant of a 2x2 matrix in the context of the script?
-In the context of the script, the determinant of a 2x2 matrix is found by multiplying the top left element by the bottom right element and subtracting the product of the top right element and the bottom left element.
How does the process of inverting a matrix relate to computational intensity?
-The process of inverting a matrix is computationally intensive because it involves multiple steps of calculating determinants, constructing matrices of minors and cofactors, and finally dividing by the determinant. This complexity increases exponentially with the size of the matrix.
What is the significance of the size of the matrix in the inverting process?
-The size of the matrix significantly impacts the complexity and time required for the inverting process. Larger matrices, such as 4x4 or 5x5, make the process more difficult, time-consuming, and prone to errors, which is why it's often preferred to use computational tools for such tasks.
Outlines
🤔 Inversion of a 3x3 Matrix
The speaker begins by expressing their dislike for manually inverting a 3x3 matrix, noting its computational intensity and the potential for errors. They explain that while this method can solve systems, it's more efficient to use a computer. The speaker then describes the process of constructing a matrix of minors, which involves crossing out the corresponding row and column for each element and replacing it with the determinant of the remaining elements. They provide a step-by-step guide on how to create this matrix, including the calculations needed for each minor. The speaker emphasizes the importance of attention to detail to avoid mistakes, and they proceed to calculate the determinants for each minor, demonstrating the process of inverting the matrix.
📝 Calculation of the Cofactor Matrix
Continuing from the previous paragraph, the speaker now focuses on obtaining the cofactor matrix from the matrix of minors. They explain that this is achieved by applying a checkerboard pattern of positive and negative signs to the minors. The speaker goes through the process of evaluating each minor to get numeric values and then signs them according to the checkerboard pattern. They detail the calculations for each element, resulting in the cofactor matrix. The speaker emphasizes the significance of this step, as it paves the way for finding the inverse of the matrix. They conclude by mentioning that the final step would be to multiply the cofactor matrix by the reciprocal of the determinant to obtain the inverse of the original matrix.
Mindmap
Keywords
💡invert a matrix
💡computationally-intensive
💡matrix of minors
💡determinant
💡cofactor matrix
💡checkerboard pattern
💡careless mistake
💡systems of equations
💡4 by 4 or 5 by 5 matrix
💡identity matrix
💡determinant of two-by-twos
Highlights
The process of inverting a 3x3 matrix by hand is introduced as computationally intensive and prone to errors.
A matrix of minors is constructed to begin the inversion process.
The speaker methodically crosses out rows and columns to find the minors, which involve calculating determinants of 2x2 matrices.
Each element of the original matrix is replaced with the determinant of the remaining elements after crossing out the respective row and column.
Step-by-step determination of minors is emphasized to minimize careless errors.
The process is detailed for all nine elements of the 3x3 matrix, showing a meticulous approach to matrix inversion.
The determinants of the 2x2 matrices are calculated to form the matrix of minors.
The speaker switches colors frequently in their demonstration to keep the elements distinct and clear.
External distractions are mentioned, highlighting the concentration required for accurate calculation.
The numeric values of the matrix of minors are finalized, converting the determinants into actual numbers.
A checkerboard pattern is used to determine the signs for the cofactor matrix, illustrating an important step in matrix inversion.
The cofactor matrix is formed by applying the checkerboard sign pattern to the matrix of minors.
Positive and negative signs are applied systematically to the elements of the cofactor matrix based on their positions.
The final steps towards finding the matrix inverse are outlined, emphasizing the application of the determinant of the original matrix.
The detailed, step-by-step tutorial concludes with a discussion of the final calculation to obtain the inverse matrix, highlighting the mathematical journey involved.
Transcripts
Browse More Related Video

Classic video on inverting a 3x3 matrix part 1 | Matrices | Precalculus | Khan Academy

Inverse of a 3x3 Matrix | Co-factor Method

Inverting 3x3 part 2: Determinant and adjugate of a matrix | Matrices | Precalculus | Khan Academy

Inverse of a 3x3 Matrix - (THE SIMPLE WAY)
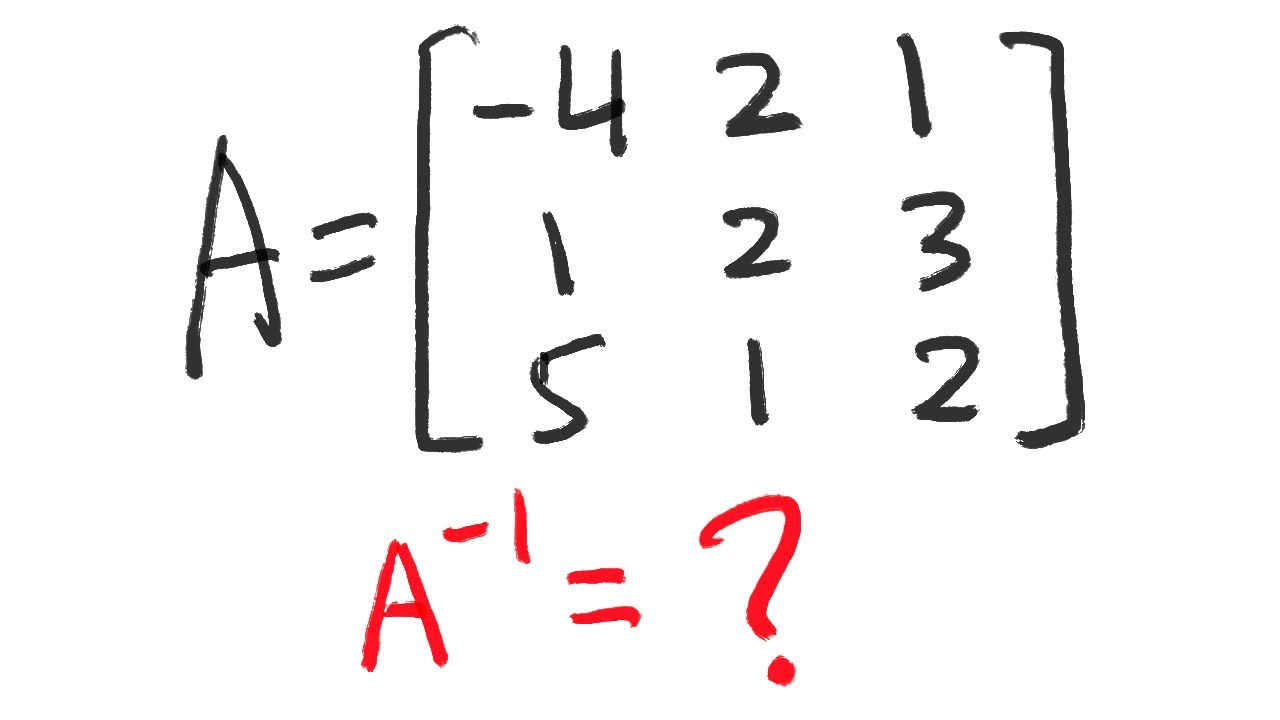
How to find the inverse of a 3 by 3 matrix (3 methods you need to know)
How To Find The Determinant of a 3x3 Matrix
5.0 / 5 (0 votes)
Thanks for rating: