Inverting 3x3 part 2: Determinant and adjugate of a matrix | Matrices | Precalculus | Khan Academy

Khan Academy
13 Jul 201506:22
EducationalLearning
32 Likes 10 Comments

TLDRThe video script outlines the process of finding the inverse of a three-by-three matrix, emphasizing the calculation of the determinant and the use of the adjugate matrix. It demonstrates two methods for computing the determinant and proceeds to detail each step in deriving the inverse matrix, ultimately highlighting the complexity of the task and suggesting that it might be better suited for computational tools rather than traditional algebra courses.

Takeaways
  • 🧩 The goal is to find the inverse of a 3x3 matrix.
  • 🔍 The first step is to calculate the determinant of the matrix.
  • 📐 There are multiple methods to find the determinant; one involves using cofactors.
  • 🤔 Another technique is to rewrite the first two columns and use diagonal products.
  • 🧮 The determinant calculation results in the value of 23 for the given matrix.
  • 🔄 The inverse of a matrix is obtained by taking the transpose of the cofactor matrix, also known as the adjugate.
  • 📈 The adjugate is found by turning rows into columns and dividing each element by the determinant.
  • 🏁 The home stretch involves multiplying 1/determinant (1/23) with the adjugate.
  • 📝 The final result is the inverse matrix, with specific elements like 1/23, 18/23, and 3/23.
  • 💻 The process is tedious and better suited for a computer, potentially not ideal for an Algebra 2 curriculum.
  • 🎓 The script suggests that such matrix inversion should not be a typical part of math education due to its abstract nature.
Q & A

  • What is the main topic of the transcript?

    -The main topic of the transcript is the process of finding the inverse of a three-by-three matrix.

  • How many techniques were mentioned for finding the determinant of a matrix?

    -Two techniques were mentioned for finding the determinant: one involves taking the product of the cofactors of the top row and summing them, and the other involves rewriting the first two columns and calculating the determinant using the top left diagonals.

  • What is the first method for finding the determinant?

    -The first method involves multiplying each element of the top row by its corresponding cofactor and then summing these products.

  • What is the second method for finding the determinant?

    -The second method involves rewriting the first two columns, calculating the product of the top left diagonals, summing them, and then subtracting the product of the top right diagonal to the bottom left.

  • What is the determinant of the given matrix C?

    -The determinant of the given matrix C is 23.

  • What is the formula for finding the inverse of a matrix?

    -The formula for finding the inverse of a matrix is 1 over the determinant times the adjugate (transpose of the cofactor matrix).

  • What is the adjugate of a matrix?

    -The adjugate of a matrix is the transpose of its cofactor matrix.

  • How is the adjugate of matrix C calculated?

    -The adjugate of matrix C is calculated by taking the transpose of the cofactor matrix, where each row becomes a column.

  • What is the final result of the inverse of matrix C?

    -The final result of the inverse of matrix C is a matrix with elements 1/23, 18/23, -4/23, -7/23, -11/23, 5/23, 5/23, and -2/23.

  • Why does the speaker suggest that finding the inverse of a matrix should not be part of a typical Algebra 2 curriculum?

    -The speaker suggests that finding the inverse of a matrix should not be part of a typical Algebra 2 curriculum because it tends to be taught in a non-contextual way, which may not be as effective for understanding.

  • What does the speaker imply about the use of computers for finding the inverse of a matrix?

    -The speaker implies that using computers to find the inverse of a matrix is more efficient and preferable over manual calculation, as it reduces the chances of making errors.

Outlines
00:00
📊 Determining the Inverse of a 3x3 Matrix

This paragraph delves into the process of finding the inverse of a 3x3 matrix. It begins by discussing the calculation of the determinant, which is a crucial step in the inversion process. The speaker explains two techniques for finding the determinant: one involves taking the top row of the matrix and multiplying each term by its corresponding cofactor and summing them up, while the other technique involves rewriting the first two columns and using the product of the top-left diagonals minus the product of the top-right to bottom-left diagonals. The speaker opts for the second technique and demonstrates its application, resulting in a determinant of 23. The paragraph concludes by outlining the final steps to find the inverse, which involves taking the transpose of the cofactor matrix (adjugate) and multiplying it by the reciprocal of the determinant (1/23).

05:00
🔢 Finalizing the Inverse Calculation

The second paragraph focuses on completing the matrix inversion process. It starts by listing the elements of the adjugate matrix, which is derived from the cofactor matrix obtained in the previous paragraph. The speaker then proceeds to divide each element of the adjugate matrix by the determinant (23) to find the inverse. The resulting inverse matrix is presented with its elements as fractions, illustrating the final outcome of the matrix inversion. The speaker also reflects on the practicality of including such calculations in the Algebra 2 curriculum, suggesting that it might be better handled by a computer due to the potential for human error and the abstract nature of the process.

Mindmap
Keywords
💡inverse of a matrix
The inverse of a matrix is a fundamental concept in linear algebra that refers to finding a matrix which, when multiplied with the original matrix, results in the identity matrix. In the context of the video, the main goal is to calculate the inverse of a 3x3 matrix, which is a process that involves finding the determinant and the adjugate of the matrix.
💡determinant
The determinant of a square matrix is a scalar value that can be computed from the elements of the matrix and is used to understand the matrix's properties, such as invertibility. In the video, the determinant is calculated using two different methods: one involving the cofactors of the top row and another using the first two columns, which both yield the same result.
💡cofactor
A cofactor of a matrix is a derived matrix obtained by deleting a row and a column from the original matrix and then applying a specific pattern of signs to the remaining elements. In the context of the video, cofactors are used to calculate the determinant and subsequently the adjugate matrix, which is essential for finding the inverse of the matrix.
💡adjugate matrix
The adjugate matrix, also known as the adjoint matrix, is the transpose of the cofactor matrix of a square matrix. It plays a crucial role in finding the inverse of a matrix because the inverse is obtained by dividing the adjugate matrix by the determinant of the original matrix.
💡transpose of a matrix
The transpose of a matrix is a new matrix obtained by interchanging the rows and columns of the original matrix. This operation is essential in various matrix operations, including finding the adjugate matrix, which is the transpose of the cofactor matrix.
💡three-by-three matrix
A three-by-three matrix, also known as a 3x3 matrix, is a square matrix with three rows and three columns. It is a common type of matrix used in various mathematical and computational applications. In the video, the focus is on finding the inverse of a 3x3 matrix, which involves specific steps and calculations.
💡linear algebra
Linear algebra is a branch of mathematics that deals with linear equations, vector spaces, and matrices. It is a foundational area of study in mathematics with numerous applications in science, engineering, and computer science. The video's content is an example of a typical topic in linear algebra, specifically matrix inversion.
💡identity matrix
An identity matrix is a special square matrix with ones on the diagonal and zeros elsewhere. When multiplied by any matrix of the same size, the result is the original matrix. The identity matrix is crucial in the context of matrix inversion because the inverse of a matrix, when multiplied by the original matrix, yields the identity matrix.
💡Algebra 2
Algebra 2 is a high school mathematics course that builds upon the principles of Algebra 1, covering more advanced topics such as quadratic equations, functions, and matrices. The video's discussion of matrix inversion is a topic that could be found in an Algebra 2 curriculum, although the speaker suggests that it may be better handled by a computer due to its complexity.
💡computer-assisted calculation
Computer-assisted calculation refers to the use of computational tools or software to perform mathematical operations that may be complex, time-consuming, or prone to human error. In the context of the video, the speaker suggests that the process of manually calculating the inverse of a matrix is better suited for computer assistance.
Highlights

The quest is to find the inverse of a three-by-three matrix.

The determinant of the matrix is the first step in finding its inverse.

There are multiple techniques to calculate the determinant, such as using cofactors or rewriting columns.

The determinant calculation involves summing products of diagonals and subtracting appropriate terms.

The example demonstrates a methodical approach to simplify the matrix for easier determinant calculation.

The final calculated determinant of the matrix is 23.

The inverse of a matrix is found by taking the adjugate of the cofactor matrix and transposing it.

Each element of the adjugate matrix is divided by the determinant to find the inverse.

The process of inverting a matrix is detailed step-by-step, emphasizing precision and avoiding mistakes.

The inverse of the matrix C is given as 1/23 times the transposed cofactor matrix.

The final inverse matrix elements are calculated as fractions divided by 23.

The example concludes with the successful inversion of the three-by-three matrix.

The speaker suggests that matrix inversion is better performed by computers and may not be suitable for a typical Algebra 2 curriculum.

The transcript provides a comprehensive guide on matrix inversion, emphasizing the importance of accuracy and methodical steps.

The process is shown to be complex and time-consuming, highlighting the value of computational tools in handling such tasks.

The example serves as an educational resource for understanding the theoretical underpinnings of matrix inversion.

Transcripts

Browse More Related Video

Inverting 3x3 part 1: Calculating matrix of minors and cofactor matrix | Precalculus | Khan Academy

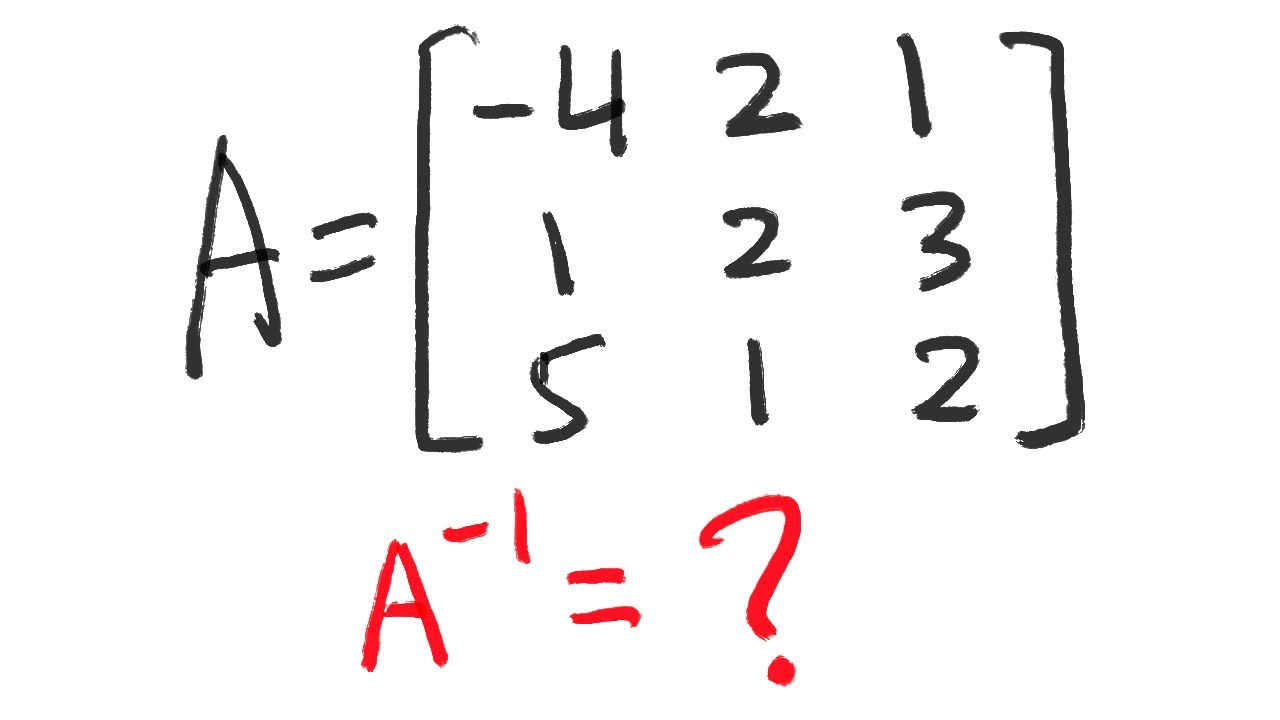
How to find the inverse of a 3 by 3 matrix (3 methods you need to know)

Classic video on inverting a 3x3 matrix part 1 | Matrices | Precalculus | Khan Academy

Inverse of 3x3 matrix

Inverse of a 3x3 Matrix | Co-factor Method

Inverse Matrices and Their Properties

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Matrix InversionDeterminant CalculationCofactor MatrixMathematics TutorialAlgebra ConceptsEducational ContentInverse ApplicationsMath PracticeLinear AlgebraComputer Algebra