Cramer's Rule Explained
TLDRThis instructional video delves into solving simultaneous equations using Cramer's Rule, applicable for 2x2, 3x3, and even 4x4 matrices. The key to this method is understanding how to calculate determinants. The video provides step-by-step examples for 2x2 and 3x3 matrices, demonstrating how to find the values of variables by forming matrices and calculating determinants. The process is clearly explained, with the video encouraging viewers to pause and attempt the calculations themselves before revealing the solutions.
Takeaways
- 📚 The Chromatic Rule is a method used to solve simultaneous equations involving systems of linear equations with matrices of various sizes, such as 2x2, 3x3, and even 4x4.
- 🔍 Understanding determinants is crucial when applying the Chromatic Rule, as it involves calculating the determinant of matrices to find the values of the variables in the equations.
- 🎯 The first step in using the Chromatic Rule is to form a matrix using the coefficients from the equations, and then find the determinant of this matrix (denoted as 'D').
- 📐 For a 2x2 system, the determinant is found by multiplying the products of the diagonals and subtracting the off-diagonal products.
- 🔢 To find the value of 'x', create a new matrix by replacing the column of 'x' coefficients with the constants from the equations, calculate its determinant (DX), and divide DX by D to get the value of 'x'.
- 📏 Similarly, for 'y', maintain the 'x' coefficients and replace the 'y' coefficients with the constants to form a new matrix, calculate its determinant (DY), and divide DY by D to find 'y'.
- 📊 For 3x3 systems, the process is more complex and involves creating three 2x2 matrices from the original 3x3 matrix, each with a different variable's coefficients replaced by the constants.
- 🤝 The values of 'x', 'y', and 'z' are found by dividing the determinants of the respective 2x2 matrices (DX, DY, DZ) by the original 3x3 matrix's determinant (D).
- 📝 It's important to practice and verify the calculations, as the accuracy of the determinants directly affects the correctness of the solution set for the variables.
- 🌟 The Chromatic Rule is a powerful tool for solving systems of linear equations, but it requires a solid grasp of matrix operations and determinant calculations to be effective.
Q & A
What is the primary focus of the video?
-The primary focus of the video is to demonstrate how to solve simultaneous equations using a method known as Cramer's rule.
What types of matrices can Cramer's rule be applied to?
-Cramer's rule can be applied to solve simultaneous equations involving matrices of sizes 2x2, 3x3, and even 4x4.
How does one begin solving a system of equations using Cramer's rule?
-To begin solving a system of equations using Cramer's rule, one must first know how to determine the determinants of the matrices involved.
What is the formula for finding the determinant of a 2x2 matrix?
-The determinant of a 2x2 matrix is found by taking the product of the entries along the main diagonal and subtracting the product of the entries along the other diagonal.
How does the video demonstrate the process of finding the determinant for a given matrix?
-The video demonstrates the process by first forming a matrix with given coefficients, then calculating the determinant using the formula for the specific size of the matrix.
What is the role of the determinant in solving simultaneous equations using Cramer's rule?
-The determinant is crucial in Cramer's rule as it helps in finding the values of the variables in the simultaneous equations by forming new matrices and calculating their determinants.
How does the video show the process of finding the values of the variables X and Y?
-The video shows the process by creating new matrices with the coefficients of the variables replaced by the constants from the equations, then calculating the determinants of these matrices and using them to find the values of X and Y.
What is the significance of the determinant 'D' in Cramer's rule?
-The determinant 'D' is the original determinant of the coefficient matrix, and it's used as a reference to find the values of the variables by dividing the determinants of the new matrices (DX, DY, etc.) by 'D'.
How does the video address the concept of finding determinants for 3x3 matrices?
-The video explains the process by first forming a 3x3 matrix, then breaking it down into smaller 2x2 matrices to calculate the determinant, which is a more complex process than for 2x2 matrices.
What is the final solution set provided in the video for a given set of determinants?
-The final solution set provided in the video is X = 7, Y = -3, and Z = -4, based on the given determinants D, DX, DY, and DZ.
What does the video suggest for viewers who are unfamiliar with finding determinants?
-The video suggests that viewers who are unfamiliar with finding determinants should first go through the provided link in the description to learn how to determine the determinants before proceeding with Cramer's rule.
Outlines
📚 Introduction to Cramer's Rule
The video begins with an introduction to Cramer's Rule, a method for solving simultaneous equations. The speaker explains that this technique can be applied to matrices of various sizes, including 2x2, 3x3, and even 4x4. The importance of understanding how to calculate determinants is emphasized, as this is a fundamental step in applying Cramer's Rule. The speaker provides a link for viewers to learn about determinants if they are unfamiliar with the concept. The video then proceeds with examples to demonstrate how to find the values of variables given by simultaneous equations.
🔢 Solving 2x2 Equations with Cramer's Rule
In this segment, the speaker focuses on solving 2x2 simultaneous equations using Cramer's Rule. The process starts with forming a 2x2 matrix using the coefficients from the equations. The determinant of this matrix (denoted as D) is calculated, which is crucial for the subsequent steps. The speaker then explains how to create two more matrices to find the values of the variables x and y. These new matrices are formed by replacing the coefficients of the variables with the constants from the equations. The determinants of these matrices (DX and DY) are calculated, and the values of the variables are found by dividing DX and DY by D. The speaker provides a worked-out example, demonstrating the steps and calculations involved in solving the equations.
📐 Expanding Cramer's Rule to 3x3 Matrices
The speaker now extends the application of Cramer's Rule to 3x3 matrices, which involves more complex calculations. The process is similar to the 2x2 case but involves additional steps and a larger matrix. The speaker explains how to form the 3x3 matrix and calculate its determinant (D). The video then details the creation of three new matrices (DX, DY, and DZ) by replacing the coefficients of the variables X, Y, and Z with the constants from the equations. The determinants of these matrices are calculated, and the values of the variables are found by dividing each determinant by D. The speaker provides a detailed example, walking through the calculations and explaining the concept of finding determinants for 3x3 matrices.
🔢 Solving 3x3 Equations with Cramer's Rule
This part of the video continues the discussion on solving 3x3 simultaneous equations using Cramer's Rule. The speaker provides a comprehensive walkthrough of the process, including the formation of the 3x3 matrix and the calculation of its determinant (D). The video then moves on to the creation of the three determinants (DX, DY, and DZ) by substituting the coefficients of the variables X, Y, and Z with the constants from the equations. The speaker demonstrates how to calculate these determinants and use them to find the values of the variables x, y, and z. The detailed calculations and step-by-step explanation help viewers understand the process of applying Cramer's Rule to 3x3 matrices.
📝 Review and Practice with Cramer's Rule
The speaker concludes the tutorial by reviewing the process of using Cramer's Rule for 3x3 matrices and encourages viewers to practice the method. The speaker provides a set of determinants (D, DX, DY, and DZ) and asks viewers to find the values of the variables X, Y, and Z using the previously explained steps. This interactive approach allows viewers to apply their understanding of the method and check their work against the speaker's forthcoming solutions. The speaker emphasizes the importance of practicing to avoid mistakes and gain proficiency in using Cramer's Rule for solving simultaneous equations.
🎓 Final Solutions and Closing Remarks
In the final segment, the speaker presents the correct solutions for the provided determinants and compares them with the solutions that viewers might have found. The speaker's solutions are X=7, Y=-3, and Z=-4, which are derived from the calculated determinants. The speaker invites viewers to ask questions in the comments section if they have any, and concludes the video with a thank you message. This closing section serves as a recap and an opportunity for viewers to clarify any doubts they may have about the application of Cramer's Rule.
Mindmap
Keywords
💡Simultaneous Equations
💡Cramer's Rule
💡Determinants
💡Matrix
💡Linear Equations
💡Coefficients
💡Variables
💡Diagonal
💡Minor Diagonal
💡Invertible Matrix
💡Substitution
Highlights
Introduction to solving simultaneous equations using Cramer's rule.
Cramer's rule is applicable for solving systems of equations with 2x2, 3x3, and even 4x4 matrices.
The importance of knowing how to determine determinants for matrices of various sizes.
Link provided in the description for those unfamiliar with finding determinants.
Explanation of forming a 2x2 matrix using coefficients from the equations.
Calculation of the determinant (d) for the 2x2 matrix.
Creation of a 2x1 matrix to find the value of x by replacing the constants in the original matrix.
Derivation of the determinant (DX) for the value of x.
Process of finding the value for y by creating a new matrix with the coefficients of y replaced.
Explanation of finding the determinant (DY) for the value of y.
Method for solving a system of equations with a 3x3 matrix using Cramer's rule.
Detailed steps for calculating the determinant of a 3x3 matrix.
Formation of matrices for DX, DY, and DZ to find the values of x, y, and z respectively.
Final solution set for the variables x, y, and z using the determinants DX, DY, DZ, and D.
Presentation of an example with given determinant values for x, y, and z.
Invitation for the audience to try solving the example and compare their results with the provided solution.
Transcripts
Browse More Related Video

Cramer's Rule - 2x2 & 3x3 Matrices - Solving Systems of Linear Equations - 2 & 3 Variables

PreCalculus - Matrices & Matrix Applications (30 of 33) Find the Determinant of a 3x3 Matrix 1

Inverse of a 3x3 Matrix | Co-factor Method

Ch. 10.6 Determinants and Cramer's Rule

Determinant of 3x3 Matrices, 2x2 Matrix, Precalculus Video Tutorial
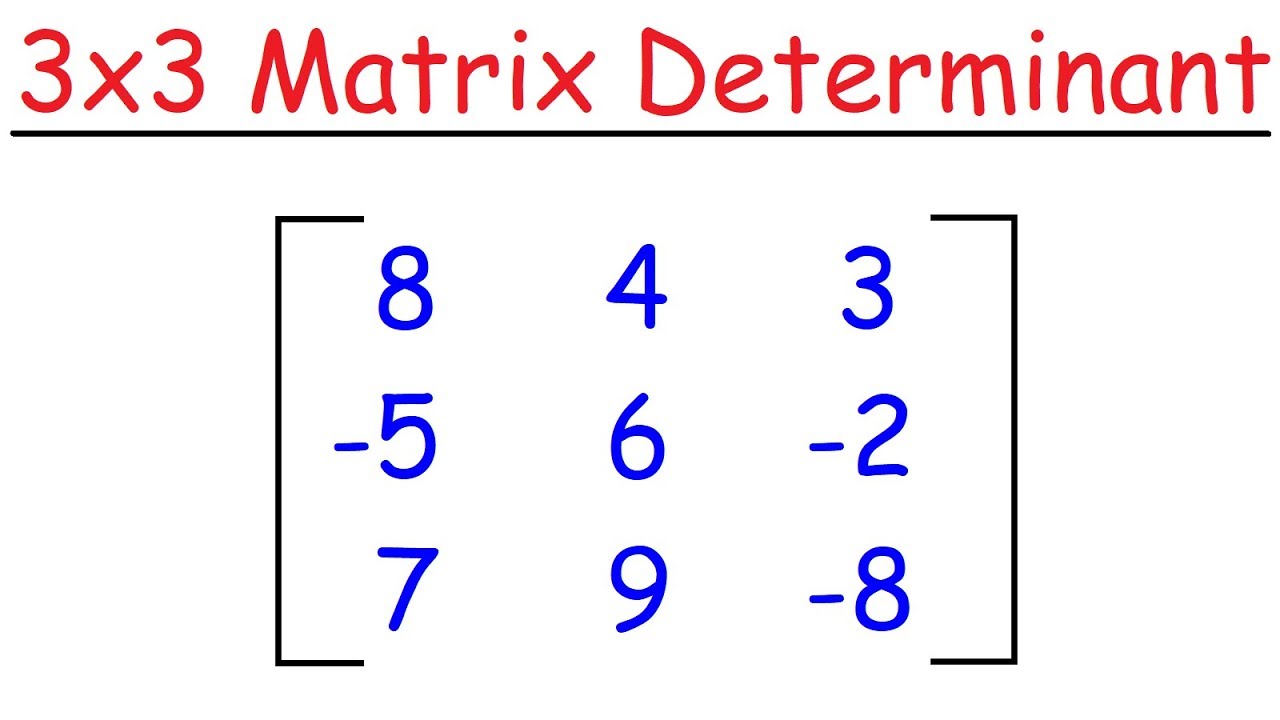
How To Find The Determinant of a 3x3 Matrix
5.0 / 5 (0 votes)
Thanks for rating: