13 - Adding Two Vectors Graphically in Physics (Vector Sum & Resultant Vectors)
TLDRThis educational video script delves into the concept of vector addition, emphasizing the importance of considering both magnitude and direction when combining vectors graphically. It explains the process through simple examples, such as pushing on a box or calculating the resultant force acting on an object. The script also touches on the commutative property of vector addition, highlighting that the order in which vectors are added does not affect the outcome. The lesson aims to transition learners from graphical methods to more practical, calculation-based approaches for solving vector problems.
Takeaways
- 📚 Vectors are quantities with both magnitude and direction, represented by arrows in physics.
- 🤝 To graphically add vectors, align them tail to head and draw a straight line from the tail of the first vector to the head of the second.
- 🔢 The resultant vector represents the combined effect of the individual vectors and is the vector you would get if you added the effects separately.
- 🎯 The direction and magnitude of the resultant vector give the overall effect of the individual vectors acting on an object.
- 🔄 Vector addition is not commutative, meaning the order in which vectors are added can affect the resultant vector.
- 📐 The graphical method of vector addition is useful for understanding the concept but may not be practical for solving complex problems.
- 🚀 Examples of vector quantities include force, displacement, velocity, and acceleration in physics.
- 🌟 The graphical addition of vectors can be used to solve problems involving multiple forces acting on an object, such as pushing a box in different directions.
- 🛤️ The resultant displacement vector does not depend on the path taken but on the overall change in position.
- 📈 In the next sections, we will learn more advanced methods for adding multiple vectors without relying solely on graphical representations.
Q & A
What is the main topic of the lesson?
-The main topic of the lesson is learning how to add two vectors graphically.
What is the difference between a scalar and a vector?
-A scalar is just a number, while a vector is a number with a direction, representing both magnitude and direction.
How are vectors represented in physics problems?
-Vectors are represented as arrows, where the length of the arrow indicates the magnitude of the vector and the direction of the arrow indicates the direction of the vector.
Why is it important to learn how to add vectors graphically?
-It is important because in physics, we often have to solve problems where multiple forces or vectors are acting on an object, and we need to find the resultant or combined effect of these vectors.
What happens when two vectors with the same magnitude and direction are added?
-When two vectors with the same magnitude and direction are added, the resultant vector will be twice as long as each of the original vectors, pointing in the same direction.
What happens when two vectors with the same magnitude but opposite directions are added?
-When two vectors with the same magnitude but opposite directions are added, they cancel each other out, resulting in a resultant vector of zero.
How do you graphically add two vectors that are at 90 degrees to each other?
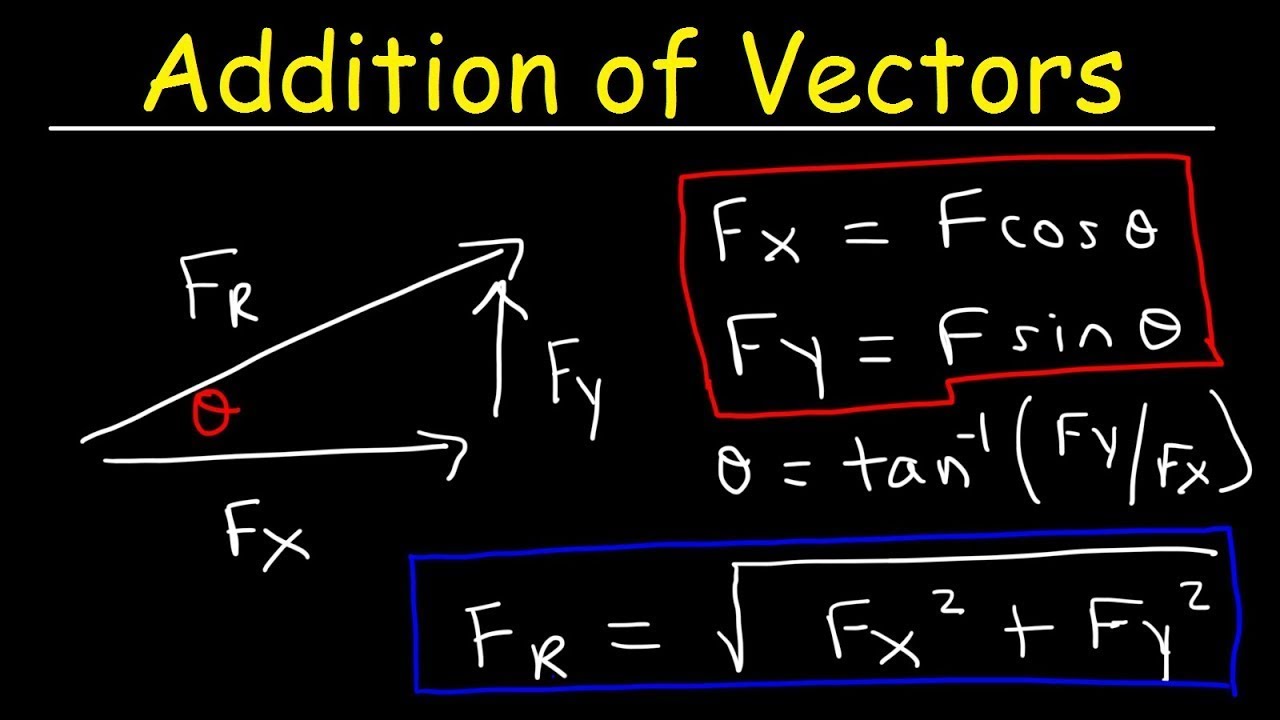
-When adding two vectors that are at 90 degrees to each other graphically, the resultant vector will be pointing at an angle that bisects the angle between the two original vectors, and its magnitude will be the square root of the sum of the squares of the magnitudes of the original vectors.
What is the graphical method for adding vectors called?
-The graphical method for adding vectors is called vector addition by the head-to-tail method, where you align the tail of one vector to the head of the other and then draw the resultant vector from the tail of the first to the head of the second vector.
What is the resultant vector?
-The resultant vector is the single vector that represents the combined effect of adding two or more vectors together.
How does the order of vector addition affect the resultant vector?
-The order of vector addition does not affect the resultant vector because vector addition is commutative, meaning that the resultant vector will be the same regardless of the order in which the vectors are added.
What are some examples of vector quantities in physics?
-Examples of vector quantities in physics include force, displacement, velocity, and electric field.
Outlines
📚 Introduction to Vector Addition
The paragraph introduces the concept of vector addition, emphasizing the importance of understanding not just the magnitude but also the direction of vectors. It explains that vectors are quantities with both magnitude and direction, represented by arrows, and that physical problems often require adding vectors together. The example of forces acting on a box illustrates the need to consider both the strength and direction of the forces to determine the box's movement. The paragraph also mentions that while the graphical method of vector addition will be covered in detail, there are other methods that will be introduced later that do not require drawing arrows.
🔍 Understanding Vector Direction and Magnitude
This paragraph delves deeper into the concept of vector direction and magnitude using the example of two people pushing a box. It explains how the direction of the force matters when adding vectors and that vectors cannot be added simply by combining their magnitudes. The paragraph uses the intuitive understanding that if two forces act in opposite directions, they cancel each other out. It also introduces the idea of resultant vectors, which are the outcome of adding two or more vectors, and emphasizes that the resultant depends on both the magnitude and the direction of the individual vectors.
🎯 Graphical Method for Vector Addition
The paragraph outlines the graphical method for adding vectors, which involves drawing and combining the vector arrows. It explains the step-by-step process of aligning the tail of one vector with the head of another to find the resultant vector. The explanation is supported by examples of different scenarios, such as forces acting at 90 degrees, forces acting at an angle, and forces with different magnitudes. The paragraph emphasizes that this method is not just for forces but applies to any type of vector, including displacement and velocity.
🤔 Reflecting on Vector Addition
This paragraph encourages reflection on the concept of vector addition. It uses the analogy of pulling a car with two chains to illustrate how the direction and magnitude of forces affect the resultant force. The paragraph also discusses the idea of resultant vectors in different situations, such as when forces are lined up, when they are at an angle, and when they are almost in the same direction. It emphasizes the importance of understanding vector addition not just as a mathematical concept but as a tool for solving real-world physics problems.
🛠️ Practical Application of Vector Addition
The paragraph discusses the practical application of vector addition in solving physics problems. It explains that instead of dealing with multiple forces, one can find a single resultant force that has the same effect on an object. This simplifies the problem and makes it easier to manage. The paragraph also introduces the notation for vector addition and provides examples with forces, velocities, and electric fields, highlighting that the addition process is the same for all types of vectors.
📈 Graphical Addition of Displacement Vectors
This paragraph focuses on the graphical addition of displacement vectors. It uses the example of walking from a front porch to a mailbox in different ways to illustrate how the resultant displacement vector remains the same, regardless of the path taken. The paragraph emphasizes that the resultant vector represents the entire trip and that there are many different ways to reach the final displacement using vector addition. It also briefly touches on the concept of velocity as a vector and how it can be added graphically, using the example of a spaceship being pushed in different directions by engines.
🔄 Commutative Property of Vector Addition
The paragraph concludes the discussion on vector addition by highlighting the commutative property of vector addition. It explains that the order in which vectors are added does not affect the resultant vector, just as the order of numbers in addition does not change the sum. The paragraph reinforces the idea that vector addition is a powerful tool for visualizing and solving physics problems, and it sets the stage for learning more advanced methods of vector addition without the need for drawing arrows.
Mindmap
Keywords
💡vector
💡scalar
💡magnitude
💡direction
💡resultant
💡commutative
💡displacement
💡velocity
💡graphical method
💡arrows
Highlights
The lesson focuses on adding two vectors graphically, providing an intuitive understanding of vector addition.
Scalars are numbers, while vectors are numbers with a direction, represented by arrows with varying lengths and orientations.
In physics, it's essential to add vectors together, such as forces acting on an object, to determine the object's motion.
Graphical vector addition is a method that involves drawing and combining vector arrows to find the resultant vector.
The magnitude and direction of a vector must both be considered when adding vectors, not just the numerical values.
The lesson provides simple examples using boxes and forces to illustrate the process of vector addition.
When two vectors have the same magnitude and are in the same direction, their resultant vector is an arrow twice as long as the individual vectors.
If two vectors have the same magnitude but are in opposite directions, they cancel each other out, resulting in a resultant vector of zero.
The lesson introduces the concept of resultant vector, which is the single vector that represents the combined effect of the individual vectors.
The graphical method of vector addition is emphasized as an essential tool for understanding, but it will be gradually phased out in favor of more practical methods.
The lesson also discusses the addition of vectors in different contexts, such as forces, velocities, and electric fields.
The process of adding vectors graphically involves aligning the tail of one vector to the head of another and then drawing a new vector from the tail of the first to the head of the second.
The direction and magnitude of the resultant vector depend on the directions and magnitudes of the original vectors, as demonstrated with various examples.
The lesson emphasizes the importance of understanding vector addition for solving physics problems, even though the graphical method will not be used extensively in practice.
The commutative property of vector addition is introduced, meaning that the order in which vectors are added does not affect the resultant vector.
The lesson concludes with a discussion on how to add more than two vectors graphically and an introduction to methods that do not require drawing arrows.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: