Reflection of light from two perpendicular flat mirror numerical
TLDRThe video script presents a geometrical problem involving the deflection of light between two perpendicular mirrors. It explains how an incident beam of light, making a 15-degree angle with the first mirror, reflects off both mirrors and determines the unknown angles using the properties of reflection and the fact that the mirrors are perpendicular to each other. The solution is methodically derived, leading to the conclusion that the outgoing beam makes a 75-degree angle with the second mirror, which is parallel to the incident beam. The explanation is clear, engaging, and encourages viewers to subscribe for more educational content.
Takeaways
- 📚 The problem is a geometrical question involving the deflection of light between two perpendicular mirrors.
- 🌟 An incident beam of light strikes the first mirror at an angle of 15 degrees.
- 🔄 The light reflects off the first mirror and hits the second mirror at a right angle since they are perpendicular.
- 🔢 The angle of reflection (theta one) equals the angle of incidence, which is 15 degrees.
- ✴️ In the right-angled triangle formed, one angle (theta two) is 90 degrees, and another (theta three) is unknown.
- 📐 By the rule that the sum of angles in a triangle equals 180 degrees, we can calculate the unknown angle (theta three) to be 75 degrees.
- 🌈 The reflected light from the second mirror will also make an angle of 75 degrees, as reflection angles are equal to incidence angles.
- 🔄 The outgoing beam of light will be parallel to the incident beam, making an angle of 15 degrees with the second mirror.
- 🎓 This problem demonstrates the application of the law of reflection and the properties of perpendicular lines.
- 💡 Understanding the relationship between incident and reflected angles is crucial for solving such problems.
- 🎥 The video provides a clear explanation and visual representation of the light's path and the angles involved.
Q & A
What is the main topic of the video script?
-The main topic of the video script is solving a geometrical problem related to the deflection of light from two perpendicular mirrors.
How does the incident beam of light interact with the first mirror?
-The incident beam of light makes an angle of 15 degrees with the first mirror, and according to the law of reflection, the angle of incidence is equal to the angle of reflection. Therefore, the light will reflect back at a 15-degree angle from the first mirror.
What is the angle between the two mirrors?
-The angle between the two mirrors is 90 degrees because the mirrors are perpendicular to each other.
How is the unknown angle (theta three) calculated?
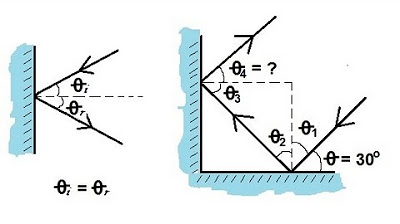
-Since all angles in a triangle add up to 180 degrees, and we know two angles (theta one is 15 degrees and theta two is 90 degrees), we can find the third angle (theta three) by subtracting the sum of the known angles from 180. So, theta three (γ) is calculated as 180 - (15 + 90) = 75 degrees.
What is the outgoing angle of the light beam after reflecting off the second mirror?
-After reflecting off the second mirror, the light beam makes an angle of 75 degrees with the second mirror, as the incident angle equals the reflected angle.
What is the relationship between the outgoing beam and the incident beam?
-The outgoing beam will be parallel to the incident beam, and they will make the same angle (15 degrees) with the second mirror.
Why is the law of reflection important in this problem?
-The law of reflection is important because it establishes that the angle of incidence is equal to the angle of reflection. This principle allows us to predict the path of the light beam after it interacts with each mirror.
What is the significance of the 90-degree angle between the mirrors?
-The 90-degree angle between the mirrors is significant because it creates a right angle, which simplifies the geometrical calculations and helps in determining the angles involved in the deflection of the light beam.
How does the video script help in understanding the concept of reflection?
-The video script provides a step-by-step explanation of how light reflects off mirrors, using a specific example with clear geometrical configurations. This helps viewers understand the principles of reflection in a practical and visual manner.
What are the practical applications of understanding light reflection from mirrors?
-Understanding light reflection from mirrors has practical applications in various fields such as optics, astronomy, and the design of mirrors for specific purposes like telescopes, periscopes, and reflective signs for safety.
How can the information in the video script be applied to real-world scenarios?
-The information in the video script can be applied to real-world scenarios like designing optical systems, understanding how light interacts with surfaces at specific angles, and creating devices that utilize the principles of reflection for various purposes.
Outlines
📚 Solving a Geometrical Optics Problem
This paragraph introduces a numerical problem involving the reflection of light between two perpendicular mirrors. The problem is based on the deflection of light from an incident beam that makes a 15-degree angle with the first mirror. The explanation emphasizes the geometrical nature of the question and outlines the steps to determine the unknown angle, theta, using basic principles of reflection and the properties of triangles. The key points include the equality of the incident and reflected angles, the 90-degree angle between the perpendicular mirrors, and the use of the triangle angle sum property to find the third angle. The solution concludes with the determination of the outgoing beam's angle with the second mirror, which is found to be 75 degrees, and the final observation that the outgoing beam will be parallel to the incident beam.
Mindmap
Keywords
💡Numerical
💡Mirors
💡Deflection of Light
💡Incident Beam
💡Reflection
💡Angle of Incidence
💡Perpendicular
💡Triangle
💡Sum of Angles
💡Law of Reflection
💡Parallel
Highlights
The problem discussed is a numerical one frequently appearing in examinations.
The scenario involves the deflection of light from two perpendicular mirrors.
The incident beam of light makes an angle of 15 degrees with the first mirror.
The mirrors are perpendicular to each other, which is a key aspect of the problem.
The light reflects off the first mirror and strikes the second one.
The angle of reflection (theta) is unknown and is the main focus of the problem.
The principle that the angle of incidence is equal to the angle of reflection is used.
The problem is purely geometrical and does not involve physical properties of light.
The incident angle with the first mirror is given as 15 degrees.
The angle between the light and the second mirror after reflection is calculated.
The sum of angles in a triangle is 180 degrees, which is used to find the unknown angle.
The third angle (theta 3) is found to be 75 degrees by subtracting from 180.
The outgoing beam's angle with the second mirror is also 75 degrees.
The outgoing beam is parallel to the incident beam, with the same angle of 15 degrees.
The problem-solving approach is clearly explained, making it easy to follow.
The video provides an engaging and educational explanation of a common geometrical problem.
The solution to the problem is presented in a step-by-step manner.
The video encourages viewers to subscribe for more educational content.
Transcripts
Browse More Related Video

Laws of Reflection | #aumsum #kids #science #education #children

The Law Of Reflection. Measuring the angle of incidence and angle of reflection.

Law of Reflection - Geometric Optics - Physics
Physics 51 - Optics: Reflections (1 of 2) Introduction
Physics 15 Torque (19 of 25) More Examples: 1 T=? of Cable Holding Fish

Ray Diagrams - Mirrors
5.0 / 5 (0 votes)
Thanks for rating: