Law of Reflection - Geometric Optics - Physics

The Organic Chemistry Tutor
10 Jan 201803:24
EducationalLearning
32 Likes 10 Comments

TLDRThis video script introduces the law of reflection, a fundamental principle stating that the angle of incidence equals the angle of reflection. Using a flat surface and a normal line as a reference, it demonstrates how a light ray striking at 30 degrees bounces back at the same angle. The script also solves a problem involving two mirrors, calculating the angles of incidence and reflection to find the angle at which a light ray exits the second mirror, concluding with the angle being 20 degrees.

Takeaways
  • 🔍 The law of reflection is the main topic of the video, explaining how light bounces off surfaces.
  • 📐 The law states that the angle of incidence is equal to the angle of reflection.
  • 📏 An example is given with a flat surface, normal line, and a light ray at an angle of incidence of 30 degrees.
  • 🤓 The angle of incidence is the angle between the light ray and the normal line.
  • 💡 The angle of reflection is the angle between the reflected light ray and the normal line, which is the same as the angle of incidence.
  • 🧭 The normal line is always perpendicular to the surface, forming a 90-degree angle with it.
  • 📐 The complementary nature of the angles is highlighted, with the sum of the angles around the normal being 90 degrees.
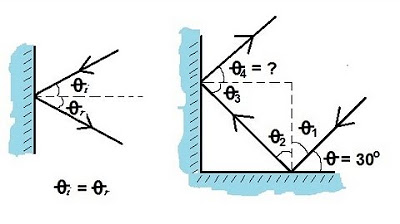
  • 📝 A problem-solving scenario is presented where a light ray strikes a mirror at an angle of 30 degrees from the horizontal.
  • 🔢 The calculation of the angle of incidence for the first mirror is demonstrated, resulting in a 60-degree angle of reflection.
  • 📐 The problem continues with determining the angle at which the light ray leaves the second mirror, involving the use of triangle angle sum property.
  • 🎯 The final calculation reveals that the light ray leaves the second mirror at an angle of 20 degrees, with the angle of reflection being 70 degrees.
Q & A

  • What is the law of reflection?

    -The law of reflection states that the angle of incidence is equal to the angle of reflection. This means that the angle at which a light ray strikes a surface is the same as the angle at which it bounces off.

  • What is the angle of incidence in the context of the law of reflection?

    -The angle of incidence is the angle between the incoming light ray and the normal line, which is perpendicular to the surface at the point of incidence.

  • How does the normal line relate to the surface in the law of reflection?

    -The normal line is always perpendicular to the surface at the point where the light ray strikes it, forming a right angle with the surface.

  • What is the complementary relationship between the angles of incidence and reflection?

    -The angles of incidence and reflection are complementary because they add up to 90 degrees when considering the normal line, which forms a right angle with the surface.

  • In the example provided, what is the angle of incidence for the light ray striking the first mirror?

    -In the example, the light ray strikes the first mirror at an angle of incidence of 30 degrees from the horizontal, which means the angle of incidence is 60 degrees with respect to the normal line.

  • What is the angle of reflection for the first mirror in the example?

    -According to the law of reflection, the angle of reflection for the first mirror is also 60 degrees, equal to the angle of incidence.

  • How is the angle of incidence for the second mirror calculated in the example?

    -The angle of incidence for the second mirror is calculated by subtracting the missing angle (y) from 90 degrees. The missing angle is found by using the fact that the sum of angles in a triangle is 180 degrees.

  • What is the missing angle y in the triangle formed by the light ray and the mirrors?

    -The missing angle y is calculated by subtracting the sum of the other two angles (30 degrees from the horizontal and 130 degrees from the first reflection) from 180 degrees, resulting in 20 degrees.

  • What is the angle of reflection for the second mirror in the example?

    -The angle of reflection for the second mirror is 70 degrees, which is equal to the angle of incidence for the second mirror.

  • What is the angle x where the light ray leaves the second mirror?

    -The angle x, where the light ray leaves the second mirror, is found by subtracting the angle of reflection (70 degrees) from 90 degrees, resulting in 20 degrees.

  • Why do the angles in the triangle formed by the light ray and the mirrors add up to 180 degrees?

    -The angles in the triangle add up to 180 degrees because they form a straight line when extended, which is a fundamental property of Euclidean geometry for any triangle.

Outlines
00:00
🔄 Law of Reflection Explained

This paragraph introduces the law of reflection, a fundamental principle in optics. It explains that the angle of incidence, the angle between the incoming light ray and the normal line to the surface, is equal to the angle of reflection, the angle between the reflected light ray and the normal. The paragraph uses an example involving a flat surface and a light ray striking it at a 30-degree angle to illustrate the concept. It emphasizes that the normal line is perpendicular to the surface and that the angles of incidence and reflection are complementary, summing up to 90 degrees.

Mindmap
Keywords
💡Law of Reflection
The law of reflection is a fundamental principle in the study of optics that describes how light behaves when it strikes a reflective surface. It states that the angle at which the light strikes the surface, known as the angle of incidence, is equal to the angle at which it reflects off the surface, known as the angle of reflection. In the video, this law is central to understanding how light rays interact with mirrors, as demonstrated in the example where a light ray strikes a surface at a 30-degree angle and reflects at the same angle.
💡Angle of Incidence
The angle of incidence refers to the angle formed between the incoming light ray and the normal line, which is an imaginary line perpendicular to the surface at the point of incidence. It is a key concept in the law of reflection and is used to predict how light will reflect off a surface. In the video script, the angle of incidence is calculated as 60 degrees when a light ray strikes a mirror at an angle of 30 degrees from the horizontal.
💡Normal Line
The normal line is an imaginary line drawn perpendicular to the surface at the point where the light ray strikes it. It serves as a reference for measuring the angle of incidence and the angle of reflection. In the context of the video, the normal line is used to determine the angles at which light rays interact with the mirror, helping to illustrate the law of reflection.
💡Angle of Reflection
The angle of reflection is the angle formed between the reflected light ray and the normal line to the surface. According to the law of reflection, this angle is equal to the angle of incidence. The video script uses this concept to explain that when a light ray reflects off a mirror, the angle at which it leaves the mirror is the same as the angle at which it arrived.
💡Flat Surface
A flat surface in the context of the video refers to a mirror or any other surface that can reflect light. The flatness of the surface is important because it ensures that the light rays will reflect in a predictable manner, following the law of reflection. The script uses a flat surface as the basis for demonstrating the behavior of light rays when they encounter a mirror.
💡Light Ray
A light ray is a straight line that represents the path of light traveling in a particular direction. In the video, light rays are used to illustrate the principles of reflection. The script describes a scenario where a light ray strikes a mirror at a certain angle and reflects off at the same angle, demonstrating the law of reflection.
💡Complementary Angles
Complementary angles are two angles that add up to 90 degrees. In the context of the video, the angles of incidence and reflection are complementary to the angle formed between the normal line and the surface. The script explains that the normal line and the surface form a right angle, making the angles of incidence and reflection complementary to each other.
💡Problem Solving
The video script includes a problem-solving scenario where the viewer is guided through the process of determining the angle at which a light ray leaves a second mirror after reflecting off a first mirror. This process involves applying the law of reflection and using geometric principles to calculate the unknown angles.
💡Triangle Angles
The script mentions that the three angles of a triangle must add up to 180 degrees. This is a fundamental principle of geometry that is used in the problem-solving part of the video to find the missing angle 'y' in the scenario involving two mirrors and a light ray.
💡Incident Ray
The incident ray is the initial light ray that strikes a reflective surface before it reflects. In the video script, the incident ray is used to demonstrate the calculation of the angle of incidence and how it relates to the angle of reflection when the light ray interacts with the first mirror.
💡Reflected Ray
The reflected ray is the light ray that has bounced off a reflective surface. The video script discusses the angle at which the reflected ray leaves the second mirror, which is a key part of understanding the overall path of the light after multiple reflections.
Highlights

The law of reflection states that the angle of incidence is equal to the angle of reflection.

The angle of incidence is the angle between the light ray and the normal line, which is perpendicular to the surface.

The angle of reflection is also between the normal line and the reflected light ray.

The normal line always forms a right angle (90 degrees) with the surface.

The angles of incidence and reflection are complementary, summing up to 90 degrees.

Example problem: A light ray strikes a mirror at an angle of 30 degrees from the horizontal.

Calculating the angle of incidence: 90 degrees minus the angle from the horizontal.

The angle of reflection for the first mirror is equal to the angle of incidence, which is 60 degrees.

Using the law of reflection to determine the angles for the second mirror.

The three angles of a triangle must add up to 180 degrees.

Calculating the missing angle (y) in the triangle formed by the light ray and mirrors.

Determining the angle of incidence for the second mirror: 90 degrees minus the missing angle (y).

The angle of reflection for the second mirror is equal to its angle of incidence, which is 70 degrees.

Calculating the angle (x) where the ray leaves the second mirror: 90 degrees minus the angle of reflection.

The reflected ray leaves the second mirror at an angle of 20 degrees.

Transcripts

Browse More Related Video

Physics 51 - Optics: Reflections (2 of 2) Inbound and Exit Ray

Laws of Reflection | #aumsum #kids #science #education #children

Physics 51 - Optics: Reflections (1 of 2) Introduction

Specular Reflection

GCSE Physics - Reflection #62

The Law Of Reflection. Measuring the angle of incidence and angle of reflection.

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Law of ReflectionPhysicsOpticsEducationalLight RaysMirrorsAnglesProblem SolvingScience VideoLearning