Understanding the Range Equation of Projectile Motion

Flipping Physics
10 Jun 201408:52
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, the concept of projectile range is introduced, explaining it as the horizontal displacement of a projectile when its overall Y displacement is zero. The range equation is derived, highlighting that the range is maximized at an initial launch angle of 45 degrees, given the same initial velocity. The importance of using consistent units and the relationship between complementary angles and their equal ranges are also discussed, providing a comprehensive understanding of projectile motion.

Takeaways
  • 📌 The range of a projectile refers to its horizontal displacement when the Y displacement is zero.
  • 📈 The range equation is derived from the horizontal component of the initial velocity and the acceleration due to gravity.
  • 🌟 The maximum range is achieved when the projectile is launched at an angle of 45 degrees.
  • 🔄 Complementary angles (e.g., 30° and 60°) result in the same range due to the symmetry of the sine function.
  • 📐 The acceleration due to gravity (g) on Earth is a positive value of 9.81 meters per second squared.
  • 🛫 The initial velocity vector includes both magnitude and direction, which is why it does not need to be resolved into components for the range equation.
  • 📊 The sine of an angle can never exceed one, which influences the maximum possible range of a projectile.
  • 🔄 The sine curve repeats every 180 degrees, but with sine(2θ), the cycle is halved to 90 degrees.
  • 🎯 The maximum height and time of flight for a projectile vary with different launch angles, even if the range is the same.
  • 📑 The range equation is R = (V_i^2 * sin(2θ_i)) / g, where R is the range, V_i is the initial velocity, θ_i is the launch angle, and g is the acceleration due to gravity.
Q & A

  • What is the definition of the range of a projectile in physics?

    -The range of a projectile in physics is the horizontal displacement of the projectile when the overall displacement in the Y direction of the projectile equals zero. It refers to the distance the object travels in the X direction at the point where it returns to its initial height.

  • Why is the range sometimes referred to as the horizontal range?

    -The range is sometimes referred to as the horizontal range because it specifically measures the horizontal displacement of the projectile, as opposed to its total displacement which includes both horizontal and vertical components.

  • What are the variables involved in the range equation for projectile motion?

    -The variables involved in the range equation are R (the range of the projectile), V sub i (the magnitude of the initial velocity vector), theta sub i (the initial angle or launch angle of the projectile), and g (the acceleration due to gravity on Earth).

  • How does the value of g, the acceleration due to gravity, affect the range equation?

    -The value of g (9.81 m/s^2 on Earth) is a constant in the range equation and affects the calculation of the range by being in the denominator. A higher value of g would result in a shorter range for a given initial velocity and angle, while a lower value would result in a longer range.

  • What is the maximum value for the sine function, and how does it relate to the range equation?

    -The maximum value for the sine function is 1. In the context of the range equation, this means that the maximum range is achieved when the sine of two times the launch angle is at its maximum, which occurs at 45 degrees or π/4 radians.

  • What is the significance of complementary angles in the context of projectile motion?

    -Complementary angles, which are two angles that add up to 90 degrees, are significant in projectile motion because they result in the same range, given the same initial velocity magnitude. For example, launch angles of 30 and 60 degrees, or 75 and 15 degrees, will produce the same range.

  • How does the shape of the sine theta graph relate to the range equation?

    -The shape of the sine theta graph is crucial for understanding the range equation because it shows how the sine function behaves with respect to different angles. In the range equation, we deal with the sine of two times the launch angle, which results in two full cycles of the sine wave within 360 degrees, with a maximum at 45 degrees.

  • What are the units for the variables in the range equation?

    -The units for the variables in the range equation are meters for R (range), meters per second for V sub i (initial velocity), and the acceleration due to gravity g is 9.81 meters per second squared. The initial angle can be in either degrees or radians, but the calculator mode should match the units used.

  • What happens to the range if the launch angle is not 45 degrees?

    -If the launch angle is not 45 degrees, the range will be smaller. This is because the maximum range is achieved at a launch angle of 45 degrees, and deviating from this angle results in a lower sine value for two times the launch angle, leading to a reduced range.

  • How does the initial velocity magnitude affect the range of the projectile?

    -The initial velocity magnitude directly affects the range of the projectile. The larger the initial velocity, the longer the range will be, assuming the same launch angle and considering the acceleration due to gravity remains constant. This relationship is quadratic, as seen in the range equation where the initial velocity is squared.

  • What is the relationship between the launch angle and the maximum height achieved by the projectile?

    -The launch angle affects the maximum height achieved by the projectile. A larger initial angle results in a higher maximum height, and consequently, the projectile will spend more time in motion before returning to its initial height. This is because the vertical component of the velocity is affected by the launch angle, with steeper angles leading to greater vertical displacements.

Outlines
00:00
📚 Introduction to Projectile Motion and Range Equation

This paragraph introduces the concept of projectile motion, specifically focusing on the range equation. Mr. P explains that the range is the horizontal displacement of a projectile when its overall displacement in the Y direction is zero. The discussion involves clarifying misconceptions about the motion in the Y direction and the conditions for the total displacement to be zero. The variables in the range equation are defined, including the initial velocity (V sub i), the launch angle (Theta sub i), and the acceleration due to gravity (g). The equation is expressed as R equals the initial velocity squared times the sine of two times the launch angle, divided by g. The importance of using consistent units and the maximum value of the sine function for achieving maximum range are also discussed. The paragraph concludes with the determination that a launch angle of 45 degrees will yield the maximum range for a given initial velocity.

05:05
📈 Understanding the Sine Function and Complementary Angles in Projectile Motion

This paragraph delves deeper into the sine function's role in the range equation and how it relates to the launch angle. The shape of the sine theta graph is reviewed, highlighting the maximum value at 45 degrees and the cyclical nature of the sine function. The concept of complementary angles is introduced, explaining that angles which are complementary (adding up to 90 degrees) will result in the same range. This is demonstrated both graphically and mathematically, with the sine of two times the initial angle equating to the sine of two times (90 minus the initial angle). The paragraph also compares projectile motion parabolas for various launch angles with the same initial velocity, emphasizing that while certain angles yield the same range, they follow different paths and have different maximum heights and durations in motion. The summary reinforces the key points about the range equation, the significance of the launch angle, and the impact of complementary angles on the range.

Mindmap
Keywords
💡Projectile Motion
Projectile motion refers to the motion of an object that is launched into the air and moves under the influence of gravity and air resistance (if considered). In the video, this concept is central as it discusses the physics behind how an object moves when thrown or launched, focusing on the horizontal displacement of the projectile when it reaches the same height from where it was launched.
💡Range Equation
The range equation is a mathematical formula used to calculate the maximum horizontal distance an object in projectile motion will travel before it hits the ground. It is derived from the equations of motion and incorporates the object's initial velocity, launch angle, and the acceleration due to gravity. In the video, the range equation is introduced to help understand how to calculate the range of a projectile.
💡Horizontal Displacement
Horizontal displacement is the change in position of an object in a horizontal direction. In the context of projectile motion, it is the distance the object travels along the ground before it lands. The video emphasizes the importance of horizontal displacement in determining the range of a projectile, which is the maximum horizontal distance achieved by the object.
💡Acceleration Due to Gravity
Acceleration due to gravity is the constant rate of change of velocity that an object experiences due to the gravitational pull of the Earth. On the surface of the Earth, it is approximately 9.81 meters per second squared, directed downwards. In the video, this value is crucial for calculating the range of a projectile, as it affects the object's vertical motion.
💡Initial Velocity
Initial velocity, often denoted as V_i, is the speed at which an object is launched or thrown. It includes both the magnitude (speed) and the direction of the velocity vector. In the context of projectile motion, the initial velocity influences both the horizontal and vertical components of the object's motion, and thus affects the range.
💡Launch Angle
The launch angle, also known as the initial angle, is the angle between the initial velocity vector and the horizontal direction when the object is launched or thrown. It plays a significant role in determining the trajectory of the projectile and, consequently, its range. The video explains how varying the launch angle affects the range and identifies the angle that maximizes it.
💡Sine Function
The sine function is a trigonometric function that relates the ratio of the opposite side to the hypotenuse in a right-angled triangle to the angle in that triangle. In the context of the range equation, the sine function is used to calculate the component of the initial velocity that contributes to the horizontal motion of the projectile.
💡Complementary Angles
Complementary angles are two angles whose sum is 90 degrees. The concept is important in the context of projectile motion because it reveals that certain angles, which are complementary, will result in the same range despite being different.
💡Maximum Range
Maximum range is the greatest horizontal distance that a projectile can travel before landing. It is determined by optimizing the launch angle and initial velocity in such a way that the projectile's trajectory results in the longest possible horizontal displacement.
💡Trigonometry
Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles, particularly right-angled triangles. In the context of projectile motion, trigonometry is used to analyze and calculate the motion of the projectile by relating the angles and the components of the initial velocity to the object's trajectory.
💡Dimensions and Units
Dimensions and units are fundamental concepts in physics that describe the physical quantities and their magnitudes. In the context of the video, it is important to use consistent dimensions and units for the initial velocity, the range, and the acceleration due to gravity to ensure the calculations are accurate.
Highlights

Introduction to the concept of projectile motion range

Definition of range as horizontal displacement when Y displacement is zero

Explanation of the variables involved in the range equation

Clarification on the importance of the initial angle for achieving maximum range

Discussion on the significance of the initial velocity's magnitude

Understanding the role of gravity in projectile motion with the value of g on Earth

Maximizing range by setting the sine of double the launch angle to its maximum value

The revelation that a 45-degree launch angle results in the maximum range

Explanation of the relationship between sine values and the launch angle for optimal range

Discussion on the dimensions required for the range and initial velocity

Clarification on the use of degrees or radians for the initial angle and ensuring calculator mode matches

Illustration of the sine curve and its impact on the range equation

Demonstration that complementary angles (e.g., 30 and 60 degrees) yield the same range

Comparison of projectile motion paths for different launch angles with the same initial velocity

Explanation of how larger initial angles affect the maximum height and time of projectile motion

Summary of the key components of the range equation and the conditions for maximum range

Engagement of the class in understanding the principles of projectile motion and range optimization

Transcripts

Browse More Related Video

Why Does 45º Launch Angle Give Maximum Range? // HSC Physics

NEET Physics | Projectile Motion | Theory & Problem-Solving | In English | Misostudy

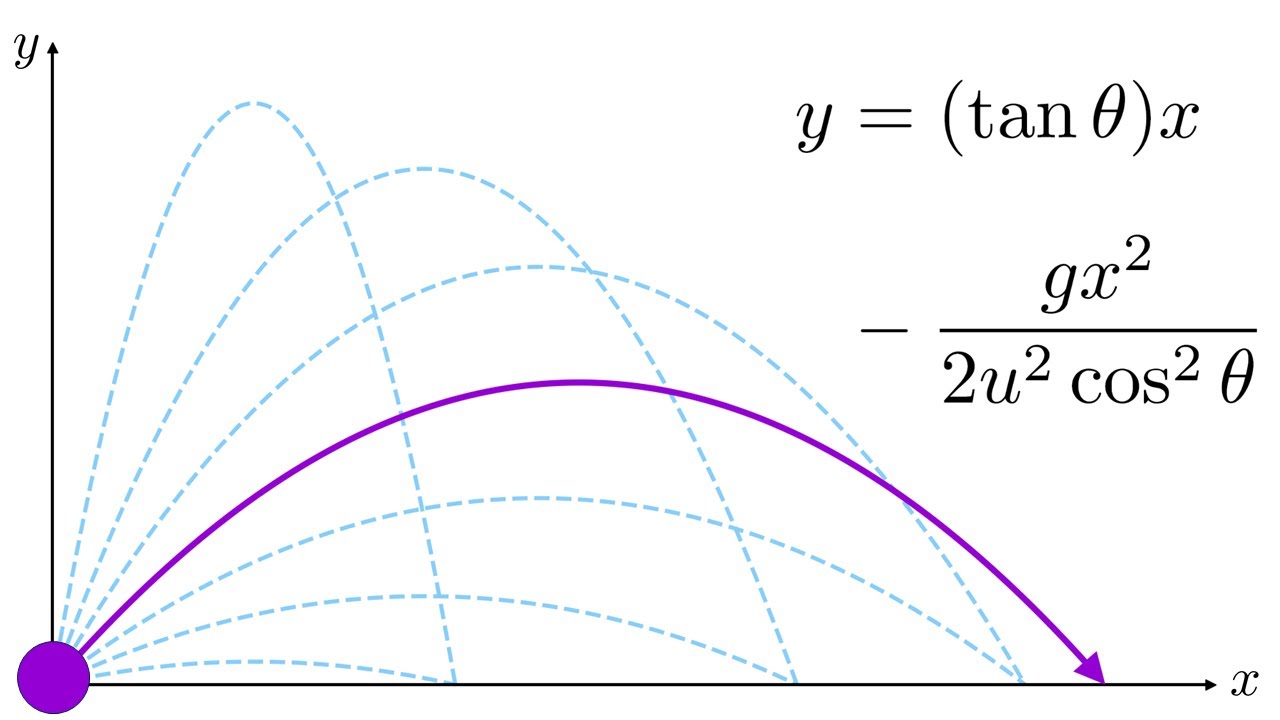
Trajectory of a projectile without drag

Projectile Motion: Finding the Maximum Height and the Range

AP Physics B Kinematics Presentation #82

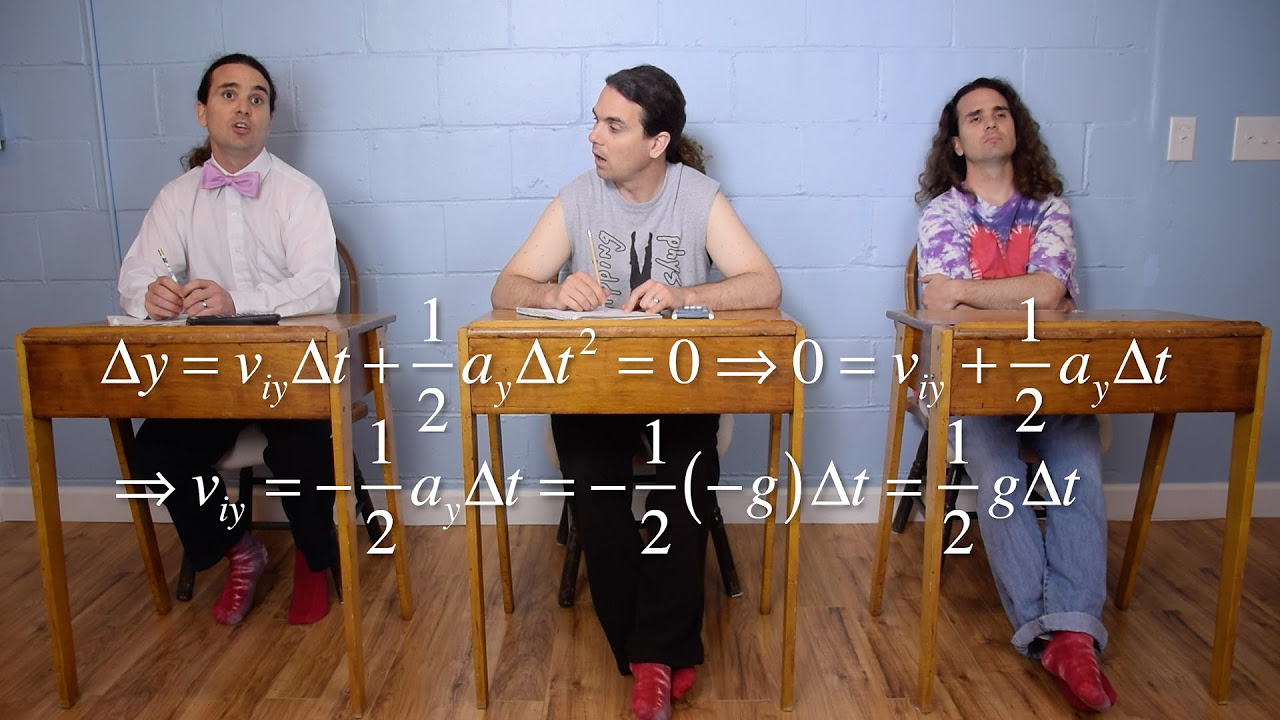
Deriving the Range Equation of Projectile Motion

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Projectile MotionPhysics ConceptsRange EquationOptimal LaunchEducational ContentInteractive LearningMathematicsPhysics EducationSine FunctionsComplementary Angles