How to calculate the angle of projection - Projectile Motion
TLDRThe video script presents a detailed analysis of a projectile motion problem, where an object is launched from level ground, reaches a peak height of 7.5 meters, and lands 10 meters away. The focus is on deriving and applying formulas for vertical and horizontal displacement to find the angle of projection. By equating and solving for velocity expressions from both displacement formulas, the video guides viewers through the mathematical process, ultimately using trigonometric identities to determine the projection angle as 71.6 degrees.
Takeaways
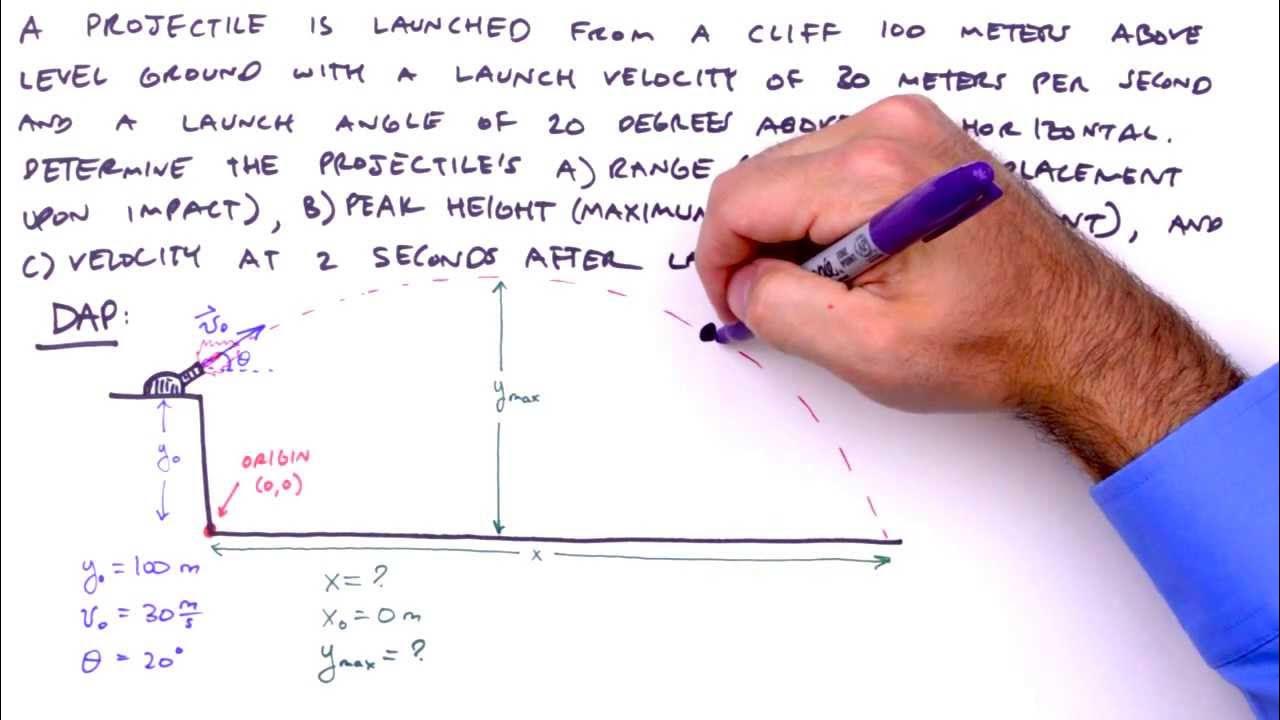
- 📌 The problem discussed involves a projectile launched from level ground with its peak height and horizontal distance given.
- 🎯 The projectile reaches a maximum height of 7.5 meters and lands 10 meters away from the launch point.
- 🔍 The goal is to find the angle of projection for the object, which is not directly provided in the problem.
- 📐 Two key formulas are used: one for vertical displacement (height) and another for horizontal displacement (range).
- 👓 The vertical displacement formula is h = (V^2 * sin^2(θ)) / (2 * g), where h is the height, V is the velocity, θ is the angle, and g is the acceleration due to gravity.
- 🏁 The horizontal displacement formula is R = (V^2 * sin(2θ)) / g, where R is the range.
- 🔢 By making velocity (V^2) the subject in both formulas, we can solve for the angle of projection (θ) without knowing the velocity's actual value.
- 🔍 The process involves equating the two formulas and eliminating V^2 to solve for θ using the given values of height and range.
- 📐 After simplification and using trigonometric identities, we find that tan(θ) = (4 * H) / R.
- 📊 By substituting the given values (H = 7.5 m, R = 10 m), we determine that tan(θ) = 3.
- 📈 The angle of projection (θ) is found by taking the inverse tangent (arctan) of 3, which results in θ = 71.6 degrees.
Q & A
What type of projectile motion is being discussed in the script?
-The script discusses the motion of a normal projectile launched from level ground and landing on level ground.
What are the given parameters for the projectile motion problem?
-The given parameters are a maximum height of 7.5 meters and a horizontal displacement of 10 meters.
What is the significance of the height and horizontal displacement in this problem?
-The height and horizontal displacement are used to derive the formulas for vertical and horizontal motion, which are essential for finding the angle of projection.
How is the angle of projection determined in the script?
-The angle of projection is determined by using the formulas for vertical displacement and horizontal displacement, and solving for the angle using the given values of height and range.
What is the formula for vertical displacement in the context of the script?
-The formula for vertical displacement is given by h = (V^2 * sin^2(θ)) / (2 * g), where h is the height, V is the velocity, θ is the angle of projection, and g is the acceleration due to gravity.
What is the formula for horizontal displacement in the context of the script?
-The formula for horizontal displacement is given by R = (V^2 * sin(2θ)) / g, where R is the range and other variables are as previously defined.
Why is it important to derive the formulas for vertical and horizontal displacement?
-Deriving the formulas is important because it allows for a better understanding of the motion and enables the calculation of the angle of projection given certain conditions.
How does the script handle the situation where the velocity is not given?
-The script makes velocity the subject of the formulas and uses the given height and range to solve for the angle of projection without directly needing the velocity value.
What trigonometric identities are used in the process of solving for the angle of projection?
-The script uses the double angle identity (sin(2θ) = 2sin(θ)cos(θ)) and the tangent identity (tan(θ) = sin(θ)/cos(θ)) to solve for the angle.
What is the final calculated angle of projection?
-The final calculated angle of projection is 71.6 degrees.
How can the audience access more information on deriving the formulas?
-The audience can follow a link provided in the video description or comment section to learn how to derive the formulas used in the problem.
What is the role of acceleration due to gravity (g) in the formulas?
-The acceleration due to gravity (g) is a constant that appears in both the vertical and horizontal displacement formulas, affecting the calculation of the projectile's motion.
Outlines
📐 Projectile Motion Analysis
This paragraph discusses the analysis of projectile motion, specifically focusing on a scenario where an object is launched from level ground and lands on the same level. The main theme revolves around the problem of finding the angle of projection given the maximum height and horizontal displacement of the projectile. The speaker emphasizes the importance of understanding how to derive the formulas used for vertical displacement and horizontal displacement. A rough diagram is introduced to visually represent the problem, and the process of using the given formulas to find the angle of projection is explained in detail.
🧮 Solving for the Angle of Projection
The second paragraph continues the discussion on projectile motion by delving into the mathematical process of solving for the angle of projection. The speaker uses the given height and range to form two equations and then manipulates these equations to eliminate the unknown velocity. By comparing and combining the equations, the speaker derives a relationship between the variables. The use of trigonometric identities, such as the double angle formula and the tangent function, is highlighted to solve for the angle. The final result is the angle of projection, calculated as the arctangent of the ratio of 4 times the height to the range, which is found to be approximately 71.6 degrees.
Mindmap
Keywords
💡Projectile Motion
💡Peak Height
💡Horizontal Displacement
💡Acceleration Due to Gravity
💡Velocity
💡Angle of Projection
💡Trigonometry
💡Derived Formulas
💡Sine and Cosine Functions
💡Tangent Function
💡Double Angle Identity
Highlights
The problem discussed involves a projectile launched from level ground and landing on the same level ground.
The projectile reaches a maximum height of 7.5 meters at the peak of its trajectory.
The horizontal distance from the point of launch to where it lands is 10 meters.
The goal is to find the angle of projection given the height and horizontal displacement.
The vertical displacement formula used is h = (V^2 * sin^2(θ)) / (2 * g), where h is the height, V is the velocity, θ is the angle, and g is the acceleration due to gravity.
The horizontal displacement or range formula is R = (V^2 * sin(2θ)) / g.
The process involves deriving formulas, which is important for solving such problems.
A video link is provided for those who need to understand how to derive the formulas.
The method starts by making velocity the subject of the formulas to eliminate it from the equations.
By equating the two formulas and simplifying, the value of θ can be found using trigonometric identities.
The double angle formula for sine is used, which is sin(2θ) = 2 sin(θ) cos(θ).
The final step involves solving for θ using the tangent function and the given values for height and range.
The angle of projection is found to be the tan inverse of 3, which is approximately 71.6 degrees.
The explanation is clear and detailed, guiding the audience through the physics and mathematics involved in solving the problem.
The use of trigonometric identities and the process of elimination are emphasized as key to solving the problem.
The practical application of the problem is understanding the motion of a projectile launched from level ground.
The problem and its solution are relevant to the study of physics and can be applied in various real-world scenarios.
The transcript provides an educational and informative walkthrough for those interested in learning about projectile motion.
The solution process is engaging and encourages the audience to follow along and understand the steps involved.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: