Ka - calculating the pH of a weak acid

Allery Chemistry
19 Oct 201407:55
EducationalLearning
32 Likes 10 Comments

TLDRThe video script by Chris Harris from alerts.com explains the process of calculating the pH of a weak acid using the Ka constant. It emphasizes the importance of understanding the dissociation of weak acids and the assumption that the concentrations of H+ and A- are equal at equilibrium. The example calculation demonstrates how to use the Ka expression and the relationship between H+ concentration and pH. The video also highlights the impact of temperature on Ka and the importance of verifying the sensibility of the calculated pH value.

Takeaways
  • 📚 The video discusses the calculation of pH for weak acids, highlighting the importance of the Ka constant.
  • 🌟 Ka is the acid dissociation constant, a key factor in determining the pH of weak acids due to their partial dissociation in solution.
  • 🔄 Weak acids do not fully ionize, leading to an equilibrium that lies to the left, meaning the concentration of H+ does not equal the concentration of the weak acid.
  • 📈 The Ka expression is set up as the ratio of products (H+ and the conjugate base) to the reactant (the weak acid), similar to the equilibrium constant Kc.
  • 🤔 An assumption is made that the concentrations of H+ and the conjugate base are equal when a weak acid dissociates, simplifying the Ka expression for pH calculation.
  • 🧪 The example given involves calculating the pH of a 0.01 moles per DM Cub of ethanoic acid with a Ka value of 1.15 * 10^-5 at a fixed temperature.
  • 🌡️ The process of finding the pH involves rearranging the Ka expression to solve for H+ concentration, taking the square root to find H+, and then using the pH formula to calculate the final pH value.
  • 📊 The calculated pH of the given example is 3.48, which is consistent with expectations for a weak acid, typically ranging between 2 to 3.
  • ⚠️ It's crucial to check the calculated pH value for sensibility; if it's greater than 7, there's likely an error in the calculation.
  • 📝 Understanding the assumptions and the reasoning behind them is essential, as they may be examined in an academic setting.
  • 🎓 The video provides a clear and concise method for calculating the pH of weak acids, emphasizing the step-by-step approach and the importance of accuracy and verification in the process.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is calculating the pH of a weak acid, with a focus on understanding and applying the Ka expression.

  • Why can't we assume that the concentration of a weak acid equals the concentration of H+?

    -We cannot assume that the concentration of a weak acid equals the concentration of H+ because weak acids dissociate weakly and do not ionize properly, resulting in a significant difference between the concentrations of the acid and the produced H+ ions.

  • What is the role of the Ka constant in the context of weak acids?

    -The Ka constant is the acid dissociation constant used to determine the extent of dissociation of a weak acid. It is the ratio of the concentrations of the products (H+ and the conjugate base) to the concentration of the reactant (the weak acid) at equilibrium.

  • What is the assumption made in the calculation of pH for weak acids?

    -The assumption made is that the concentrations of H+ and the conjugate base (A-) produced from the dissociation of the weak acid (HA) are equal, which allows us to simplify the Ka expression to Ka = [H+]/[HA].

  • How does temperature affect the Ka value?

    -The Ka value can be altered by changes in temperature, as it is a constant that is specific to a given temperature. Different temperatures can result in different Ka values for the same weak acid.

  • What is the example problem presented in the video?

    -The example problem is to calculate the pH of a 0.01 moles per liter solution of ethanoic acid (CH3COOH), with a given Ka value of 1.15 * 10^-5 at a certain temperature.

  • What is the significance of the equation pH = -log[H+] in the context of acids and bases?

    -The equation pH = -log[H+] is fundamental in understanding the acidity or basicity of a solution. It relates the pH, a measure of acidity, to the concentration of H+ ions, which are responsible for acidic properties.

  • How is the concentration of H+ squared (H+^2) related to the Ka expression?

    -In the Ka expression, [H+]^2 represents the concentration of H+ ions squared. This term is derived from the fact that the weak acid (HA) dissociates into H+ and its conjugate base (A-), and at equilibrium, the product of their concentrations equals the Ka constant times the concentration of the weak acid.

  • What is the step-by-step process for calculating the pH of a weak acid solution?

    -The process involves: 1) Establishing the Ka expression, 2) Making the assumption that [H+] = [A-], 3) Rearranging the Ka expression to solve for [H+], 4) Calculating [H+] by taking the square root of [H+]^2, and 5) Using the concentration of H+ in the pH equation to find the pH value.

  • What is the calculated pH value for the example problem?

    -The calculated pH value for the example problem is 3.48, which is a typical pH range for weak acids.

  • How can you verify if your calculated pH value is correct?

    -You can verify the correctness of your calculated pH value by checking if it falls within a sensible range for the type of acid (weak or strong) and ensuring that no mathematical errors were made during the calculation process. If the pH value is greater than 7, it indicates an error in the calculation.

Outlines
00:00
📚 Introduction to Calculating pH of Weak Acids

This paragraph introduces the topic of calculating the pH of weak acids, highlighting the importance of the Ka constant. Chris Harris explains that weak acids partially dissociate in solution, which is why the concentration of the weak acid does not equal the concentration of H+ ions. The Ka expression is introduced as a tool to determine the pH of weak acids, and an assumption is made that the concentrations of H+ and the acid's anion are equal. The paragraph sets the stage for an example calculation and emphasizes the significance of the relationship between acids, bases, and their pH values.

05:03
🧪 Example Calculation: pH of Ethanoic Acid

In this paragraph, the process of calculating the pH of a specific weak acid, ethanoic acid (CH3COOH), is detailed. The example involves a 0.01 moles per DM cubed solution of ethanoic acid at a given Ka value of 1.15 * 10^-5. The calculation involves using the Ka expression with the assumption that the concentration of H+ squared equals the Ka value times the concentration of the weak acid. After solving for H+ concentration, the square root is taken to find the actual H+ concentration. This value is then used to calculate the pH using the formula pH = -log[H+]. The resulting pH of 3.48 is a sensible value for a weak acid, and the paragraph concludes with advice on checking the reasonableness of the calculated pH value.

Mindmap
Keywords
💡pH
pH is a measure of the hydrogen ion concentration in a solution, which indicates its acidity or alkalinity. In the context of the video, calculating the pH of a weak acid is the main objective, and it is crucial to understand the relationship between pH and the concentration of H+ ions. The video explains that pH is calculated using the formula pH = -log[H+], which underscores the importance of determining the H+ concentration when working with weak acids.
💡weak acid
A weak acid is an acid that does not completely dissociate or ionize in a solution. In the video, it is emphasized that weak acids only partially release H+ ions, resulting in a lower concentration of these ions compared to strong acids. The example given is ethanoic acid (CH3COOH), which is a weak acid and has a lower pH than strong acids, typically falling in the range of 2 to 3.
💡Ka
Ka, or the acid dissociation constant, is a measure of the strength of a weak acid's ability to dissociate in solution. It is central to the video's theme as it is used to calculate the pH of weak acids. The Ka expression is given as Ka = [H+][A-]/[HA], where [HA] is the concentration of the weak acid, [H+] is the concentration of hydrogen ions, and [A-] is the concentration of the conjugate base. The video illustrates how Ka is used in the calculation process by rearranging the expression to solve for [H+].
💡dissociation
Dissociation refers to the process where a compound breaks down into its ions when dissolved in a solvent. In the context of the video, the partial dissociation of weak acids is highlighted, explaining that they do not fully break apart into ions, leading to a lower concentration of H+ ions and a higher pH value compared to strong acids. The video uses ethanoic acid as an example to demonstrate this concept.
💡equilibrium
Equilibrium in chemistry refers to the state where the rates of the forward and reverse reactions are equal, and the concentrations of the reactants and products remain constant. The video discusses that weak acids establish an equilibrium where the concentration of the undissociated acid (HA) is much greater than the concentrations of the dissociated ions (H+ and A-), which is why the Ka expression is used to describe this balance.
💡assumption
In the context of the video, an assumption is made for the simplification of calculations when dealing with weak acids. The assumption is that the concentrations of H+ and A- are equal, which allows for the rearrangement of the Ka expression to solve for the concentration of H+. This assumption is crucial for the calculation of pH in weak acids but does not apply in all scenarios, such as when calculating buffer solutions.
💡concentration
Concentration in chemistry refers to the amount of a substance present in a given volume of solution. The video emphasizes the importance of understanding the concentration of weak acids and their dissociation products, specifically the H+ ions, as this directly affects the pH calculation. The concentration of H+ is determined through the Ka expression and the assumption made about the equality of H+ and A- concentrations.
💡logarithm
A logarithm is the inverse operation to exponentiation and is used to solve for unknown values in exponential relationships. In the video, the logarithm is essential in the pH calculation formula, pH = -log[H+]. The video demonstrates how to use logarithms to find the pH value once the concentration of H+ ions is known from the Ka expression and the assumption made.
💡buffer
A buffer is a solution that resists changes in pH when small amounts of an acid or a base are added. The video mentions buffers in the context of explaining that the assumption made for weak acids (that [H+] = [A-]) does not apply to buffer solutions. Buffers are important in maintaining a stable pH environment and are the subject of other videos in the mentioned playlist.
💡temperature
Temperature can affect the value of the Ka constant for a weak acid, as mentioned in the video. The Ka value given in the example is specific to a certain temperature, and changes in temperature can alter the dissociation behavior of weak acids, thus affecting their Ka values and consequently their pH when dissolved in solution.
💡square root
The square root is a mathematical operation that undoes squaring, and it is used in the video to find the concentration of H+ ions from the squared concentration of H+ (H+^2). After rearranging the Ka expression and solving for H+^2, the square root is taken to obtain the actual concentration of H+, which is then used to calculate the pH of the weak acid solution.
Highlights

Calculating the pH of a weak acid is the main focus of the video.

Ka is the key constant used in the calculation of weak acids' pH.

Weak acids partially dissociate in solution, leading to an equilibrium that lies to the left.

The Ka expression is introduced as a method to express the acid dissociation constant.

An assumption is made that the concentrations of H+ and A- are equal when a weak acid dissociates.

The relationship between pH and H+ concentration is fundamental in acid-base chemistry.

The example calculation demonstrates the process of determining the pH of a 0.01 moles per DM^3 solution of ethanoic acid.

The value of Ka for ethanoic acid at the given temperature is 1.15 * 10^-5 moles per DM^3.

The calculation involves the rearrangement of the Ka expression to solve for the concentration of H+.

The square root of H+ squared concentration is used to find the actual H+ concentration.

The pH is calculated using the formula pH = -log[H+], where [H+] is the concentration of H+ ions.

The calculated pH for the ethanoic acid solution is 3.48, which is a typical range for weak acids.

It is important to check the sensibility of the calculated pH value to ensure accuracy.

The process of calculating the pH of a weak acid involves several steps, including establishing the Ka expression and making assumptions.

The video provides a clear and detailed explanation of each step in the calculation, making it accessible for learners.

The impact of temperature on the Ka value is acknowledged, indicating that it can change with varying conditions.

The video concludes with a summary of the procedure for calculating the pH of a weak acid, reinforcing the key points.

Transcripts

Browse More Related Video

Ka - Calculating acid concentration and Ka

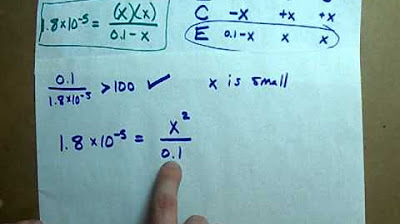
pH of a Weak Acid (0.1 M Acetic Acid) EXAMPLE

Calculating the pH of Weak Acids

Find the Ka of an acid (Given pH) (0.1 M Hypochlorous acid) EXAMPLE

Acid Dissociation Constant, Ka and pKa (A-Level Chemistry)

Calculating the pH of a buffer made from a weak acid and strong base

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Chemistry BasicspH CalculationWeak AcidsKa ConstantEquilibriumEthanoic AcidTutorial VideoAssumption AnalysisScientific MethodAcids and Bases