AP Physics 1 - Angular Momentum
TLDRIn this lesson, Dan Fullerton explains the concept of angular momentum, its conservation in closed systems, and how it compares to linear momentum. He demonstrates the calculation of angular momentum for a point particle and its dependence on the reference point. The lesson also covers how angular momentum principles apply to rotating rigid bodies and heavenly bodies, including the derivation of relationships between velocity, radius, and angular velocity in elliptical orbits, linking to Kepler's second law of planetary motion.
Takeaways
- 🌟 Angular momentum is a vector quantity, similar to linear momentum, and is the product of an object's moment of inertia and its angular velocity.
- 🔄 Conservation of angular momentum states that in a closed system with no net external torques, the total angular momentum remains constant.
- 📐 To calculate angular momentum, use the formula L = Iω (moment of inertia times angular velocity) or L = r x (mv) (cross product of position and momentum vectors).
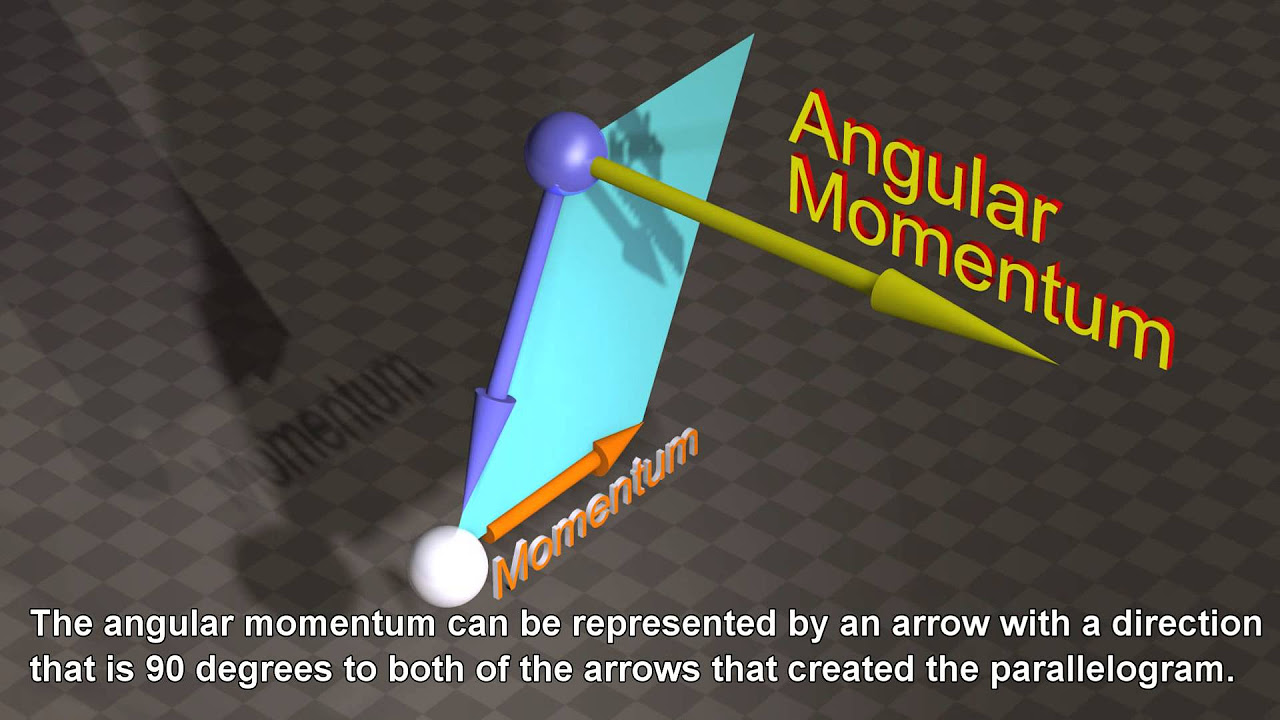
- 👉 The direction of angular momentum is determined by the right-hand rule: point fingers from the reference point towards the particle and then in the direction of the momentum vector; the thumb points in the direction of positive angular momentum.
- 🔴 The magnitude of angular momentum depends on the choice of the reference point, and different reference points can yield different values.
- 📊 When an object moves in a circular path, the magnitude of its angular momentum is given by L = mvR, where v is the linear velocity and R is the radius of the circle.
- 🌀 If two objects with different moments of inertia collide and stick together, their combined angular velocity is given by the initial angular momentum divided by the total final moment of inertia.
- 🪐 In celestial mechanics, the conservation of angular momentum principle leads to Kepler's second law, which states that a line joining a planet to the star it orbits sweeps out equal areas in equal times.
- 📉 An increase in an object's moment of inertia results in a decrease in its angular velocity, assuming no external torques are applied.
- 🔄 The total angular momentum of a system is the vector sum of the angular momenta of all its constituent particles.
- 🎓 Understanding angular momentum and its conservation is crucial for analyzing the behavior of rotating and orbiting bodies in physics.
Q & A
What is angular momentum and how does it compare to linear momentum?
-Angular momentum, denoted as L, is a vector quantity that represents the rotational equivalent of linear momentum. It is the product of an object's moment of inertia and its angular velocity about the center of mass. Linear momentum, on the other hand, is the product of an object's inertial mass and its linear velocity. Both quantities describe the motion of an object, but while linear momentum is concerned with translational motion, angular momentum deals with rotational motion.
How is the direction of angular momentum determined?
-The direction of angular momentum is determined using the right-hand rule. If you point the fingers of your right hand in the direction of the position vector from the reference point to the particle, and then bend your fingers in the direction of the object's momentum vector, your thumb will point in the direction of positive angular momentum. This is a cross product, which results in a vector perpendicular to both the position and momentum vectors.
What is the formula for calculating the magnitude of angular momentum?
-The magnitude of angular momentum (L) can be calculated using the formula L = M * V * R * sin(θ), where M is the mass of the object, V is its linear velocity, R is the position vector from the reference point, and θ is the angle between the position vector and the momentum vector. Alternatively, it can also be calculated as L = I * ω, where I is the moment of inertia and ω is the angular velocity.
How does the conservation of angular momentum principle work?
-The conservation of angular momentum states that in a closed system with no net external torques, the total angular momentum remains constant. This means that the sum of the individual angular momenta of all particles in the system remains the same over time. This principle is a fundamental concept in physics and is applicable to a wide range of phenomena, from the motion of celestial bodies to the behavior of particles in quantum mechanics.
What happens to the angular velocity of a rotating object when its moment of inertia changes?
-When the moment of inertia of a rotating object increases, its angular velocity decreases, assuming that no external torques are acting on the system. This is due to the conservation of angular momentum, which dictates that the product of the moment of inertia and angular velocity must remain constant if there are no external torques. Therefore, if the moment of inertia increases, the angular velocity must decrease to maintain the same total angular momentum.
How does the angular momentum depend on the choice of the reference point?
-The angular momentum of an object depends on the reference point from which it is measured. Different reference points can result in different values of angular momentum, as the position vector (R) and the angle (θ) between the position vector and the momentum vector will vary. This is why it's important to specify the reference point when discussing angular momentum.
What is the relationship between angular momentum and Kepler's second law?
-Kepler's second law, which states that a line joining a planet to the Sun sweeps out equal areas during equal intervals of time, is a direct consequence of the conservation of angular momentum. According to this law, the velocity of a planet in its elliptical orbit is inversely proportional to its distance from the Sun at any given point. This is because the angular momentum must be conserved, leading to faster motion at closer distances and slower motion at greater distances.
How can the formula for angular momentum be derived for an object moving in a circular path?
-For an object moving in a circular path at a constant speed, the magnitude of the angular momentum about the center of the circle (Point C) is given by L_C = M * V * R, where M is the mass, V is the linear velocity, and R is the radius of the circle. This is derived from the general formula L = I * ω by recognizing that for uniform circular motion, the moment of inertia (I) is equal to M * R^2, and the angular velocity (ω) is given by V / R. Thus, L_C = (M * R^2) * (V / R) = M * V * R.
What is the total angular momentum of a system?
-The total angular momentum of a system is the vector sum of the individual angular momenta of all the particles within that system. Since angular momentum is a vector quantity, the total angular momentum is obtained by adding up the angular momenta of each particle, taking into account their directions as well as their magnitudes.
How does the angular momentum of a point particle depend on its position relative to the reference point?
-The angular momentum of a point particle depends on the position vector R from the reference point to the particle. The magnitude of the angular momentum is given by the product of the mass of the particle, its velocity, and the magnitude of the position vector, as well as the sine of the angle between the position vector and the velocity vector. The direction of the angular momentum is determined by the right-hand rule, which depends on the specific orientation of the position and velocity vectors relative to the reference point.
What is the significance of the conservation of angular momentum in celestial mechanics?
-The conservation of angular momentum is crucial in celestial mechanics as it governs the motion of celestial bodies, such as planets and moons, around their central bodies. It explains the stability of orbits and the relationship between the orbital speed, radius, and angular velocity of a body. This principle is also responsible for the phenomenon described by Kepler's second law, which states that a body in orbit sweeps out equal areas in equal times, leading to the conclusion that the body moves faster when it is closer to the central body and slower when it is farther away.
Outlines
🌟 Introduction to Angular Momentum
This paragraph introduces the concept of angular momentum, comparing it to linear momentum. It explains that angular momentum is a vector quantity, represented by the product of an object's moment of inertia and its angular velocity about the center of mass. The conservation of angular momentum in a closed system without external torques is discussed, as well as the formula for calculating angular momentum, which involves a cross product of the position vector and the momentum vector. The right-hand rule is used to determine the direction of angular momentum. The paragraph also presents a simple example of an object moving in a circular path to illustrate the transition between different formulas for angular momentum.
📐 Calculation and Conservation of Angular Momentum
This section delves into the calculation of angular momentum for different reference points and demonstrates how angular momentum values can vary based on the chosen reference point. It presents a sample problem involving a point particle with a given mass, position, and velocity, and shows how to calculate the angular momentum about a specific point using the sine of the angle between the position vector and the direction of velocity. The paragraph also discusses the conservation of angular momentum through two examples: one involving a person spinning on a pedestal with a change in moment of inertia, and the other involving two discs sticking together upon contact. These examples illustrate how angular momentum remains constant when no external torques are applied.
🪐 Angular Momentum in Celestial Bodies and Kepler's Laws
The final paragraph explores the application of angular momentum in the context of celestial bodies and orbits. It develops a relationship between the velocity and radius of a planet in an elliptical orbit, emphasizing the conservation of angular momentum in the absence of external torques. By analyzing the velocity and position at different points in the orbit, such as apogee and perigee, the paragraph draws a connection to Kepler's second law of planetary motion, which states that a line connecting a planet to its star sweeps out equal areas in equal times. This comparison highlights the relationship between angular momentum principles and the laws governing planetary motion.
Mindmap
Keywords
💡Angular Momentum
💡Conservation of Angular Momentum
💡Moment of Inertia
💡Linear Momentum
💡Cross Product
💡Right-Hand Rule
💡Rotational Velocity
💡Rigid Bodies
💡Elliptical Orbit
💡Kepler's Laws
Highlights
Angular momentum is a vector quantity that describes rotational motion, similar to linear momentum which describes translational motion.
The conservation of angular momentum is a fundamental principle in physics, stating that the angular momentum of a closed system remains constant when no net external torques are applied.
The formula for angular momentum (L) is given by the product of an object's moment of inertia (I) and its angular velocity (ω) about the center of mass, L = I * ω.
The direction of angular momentum is determined by the right-hand rule, which involves pointing the fingers of the right hand in the direction of the position vector and curling them towards the direction of the momentum vector, with the thumb pointing in the direction of positive angular momentum.
To calculate the magnitude of angular momentum, one can use the formula L = M * V * R * sin(θ), where M is the mass, V is the linear velocity, R is the position vector magnitude, and θ is the angle between the position and velocity vectors.
For an object moving in a circular path, the magnitude of angular momentum simplifies to L = M * V * R, as the angle (θ) between the position and velocity vectors is always 90 degrees, making sin(θ) equal to 1.
The total angular momentum of a system is the vector sum of the individual angular momenta of all particles within that system.
The example of calculating angular momentum for a 5 kg point particle located at (2, 2) with a velocity of 2 m/s to the east demonstrates how to apply the formula L = M * V * R * sin(θ) and the right-hand rule to find the magnitude and direction of angular momentum.
In the case of Abe Lincoln spinning on a rotating pedestal, the conservation of angular momentum principle is used to determine the change in angular velocity after catching an exercise ball that increases his moment of inertia.
The example of two identical discs, one spinning and one stationary, illustrates how the conservation of angular momentum can be used to find the combined angular velocity when they stick together after making contact.
Angular momentum principles can be applied to heavenly bodies, such as planets in elliptical orbits, to derive relationships between velocity and radius at different points in the orbit.
The conservation of angular momentum is linked to Kepler's second law of planetary motion, which states that a planet sweeps out equal areas in equal times, explaining why planets move faster at perihelion (closest to the star) and slower at aphelion (farthest from the star).
The lesson provides a comprehensive overview of angular momentum and its conservation, including practical applications and examples that help to deepen the understanding of these fundamental concepts in physics.
The use of the right-hand rule for determining the direction of angular momentum is a crucial concept that is emphasized in the lesson, with clear instructions on how to apply it in various scenarios.
The lesson highlights the importance of understanding the relationship between linear momentum and angular momentum, as both are key to analyzing the behavior of objects in motion, whether in translation or rotation.
The example problems provided in the lesson serve to reinforce the concepts of angular momentum and conservation of angular momentum, offering practical demonstrations of how these principles are applied in real-world situations.
The lesson emphasizes the significance of reference points in calculating angular momentum, as the value and direction of angular momentum can vary depending on the chosen reference point.
The discussion on angular momentum in celestial bodies connects the abstract concept to tangible astronomical phenomena, making the lesson more engaging and relatable.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: