AP Physics Workbook 5.N Center of Mass Motion

Mr.S ClassRoom
15 Nov 202006:39
EducationalLearning
32 Likes 10 Comments

TLDRThis video script delves into the principles of momentum and the center of mass as explored in AP Physics. It narrates a scenario involving an explosion that propels a 1kg block to the left and a 4kg block to the right, using kinematics equations and the conservation of momentum to calculate various times and velocities. The script further explains how friction affects the deceleration of the blocks and how the center of mass changes during the explosion and subsequent motion. The comprehensive explanation is supplemented with notes on calculating the center of mass, enhancing understanding of the concepts discussed.

Takeaways
  • πŸ’₯ Explosion in the center initiates motion for 1 kg and 4 kg blocks in opposite directions.
  • πŸ“ No horizontal acceleration for the initial motion due to the symmetry of the setup.
  • 🚫 Initial velocity of 1 kg block is negative (leftward), while the 4 kg block is positive (rightward).
  • πŸ”’ Time calculation for 1 kg block to hit the surface is 1 second using kinematics equations.
  • πŸŒ€ Conservation of momentum principle is applied to find the final velocity of the 4 kg block.
  • πŸƒβ€β™‚οΈ Final velocity of the 4 kg block is 10 m/s to the right after the explosion.
  • πŸ”„ Deceleration of both blocks on a rough surface is due to frictional force.
  • πŸ“‰ Frictional force equals the product of the coefficient of friction (ΞΌ) and the normal force (mg).
  • πŸ›‘ Total time for 1 kg block to come to rest is 9 seconds, combining the time to reach the surface and slide to a stop.
  • πŸ›‘ Total time for 4 kg block to come to rest is 6 seconds, combining the time to reach the surface and slide to a stop.
  • 🎯 Center of mass remains at zero initially as there is no net external force acting on the system.
  • πŸ“ˆ Center of mass increases during the explosion as the distance between the blocks increases.
Q & A

  • What is the main topic of Unit 5 in the AP Physics workbook?

    -The main topic of Unit 5 is Momentum, including the concepts of the center of mass and conservation of momentum.【3】

  • How does the explosion scenario in the unit illustrate the principle of conservation of momentum?

    -The explosion scenario demonstrates conservation of momentum by showing how the initial momentum of the system (one kilogram block and four kilogram block) is conserved after the explosion, with the 1 kg block moving to the left and the 4 kg block moving to the right.【3】

  • What is the significance of the center of mass in physics?

    -The center of mass is significant as it represents the average location of the mass of an object or system of objects. It is important in understanding the motion and balance of the system, especially during interactions like collisions.【3】

  • How does the position of the center of mass change during an explosion?

    -During an explosion, the center of mass increases because the distance between the two masses (one kilogram and four kilogram blocks) increases, causing the center of mass to move away from the original equilibrium position towards the heavier mass.【3】

  • What is the role of friction in the motion of objects as described in the script?

    -Friction plays a crucial role as a force that opposes the motion of objects. In the script, it is the only horizontal force acting on the blocks once they hit the rough surface, causing them to decelerate and eventually come to a stop.【3】

  • How is the deceleration of the blocks on a rough surface calculated?

    -The deceleration is calculated using Newton's second law (F = ma), where the force of friction (muN) is the only horizontal force, and N is the normal force (equal to mg). The acceleration is thus mu times gravity (5 m/s^2).【3】

  • What is the time it takes for the 1 kg block to hit the rough surface?

    -The time it takes for the 1 kg block to hit the rough surface is 1 second, calculated using the kinematics equation with the given initial velocity and distance traveled.【3】

  • How long does it take for both the 1 kg and 4 kg blocks to come to a complete stop?

    -It takes 9 seconds for the 1 kg block and 6 seconds for the 4 kg block to come to a complete stop, considering both the time it takes to reach the rough surface and the time it takes to slide on the surface.【3】

  • What is the initial velocity of the 4 kg block after the explosion?

    -The initial velocity of the 4 kg block after the explosion is 10 m/s to the right, determined using the conservation of momentum principle.【3】

  • How does the total time for each block to come to rest relate to the conservation of momentum?

    -The total time for each block to come to rest is determined by considering both the initial momentum and the deceleration due to friction. The conservation of momentum ensures that the total momentum before and after the explosion remains the same, guiding the calculations for the total time.【3】

  • What is the formula used to calculate the center of mass of a system?

    -The center of mass of a system is calculated using the formula (m1x1 + m2x2) / (m1 + m2), where m1 and m2 are the masses and x1 and x2 are the distances from a reference point for each mass.【3】

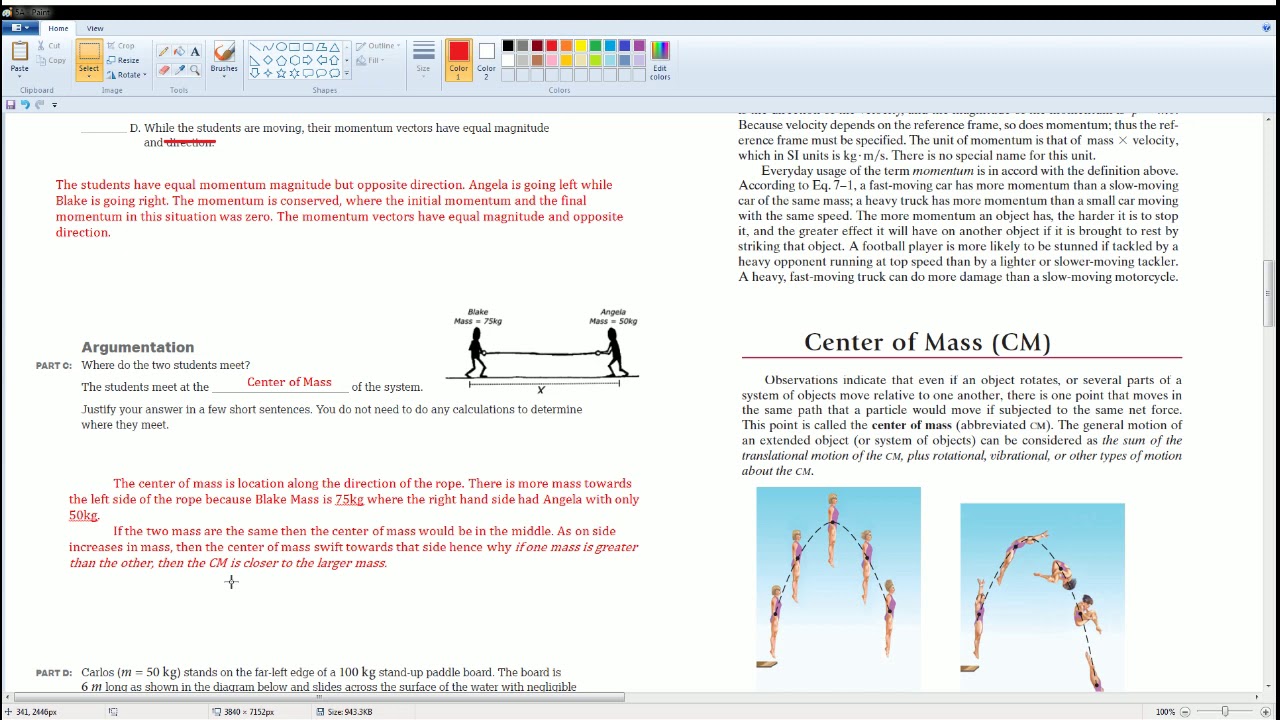
  • How does the argumentative question in the script help in understanding the concept of center of mass?

    -The argumentative question challenges the understanding of the center of mass before and during a collision, emphasizing the changes in the center of mass due to the forces acting on the system and the importance of considering these dynamics in physical analysis.【3】

Outlines
00:00
πŸ’₯ Explosion and Momentum Conservation

This paragraph introduces a scenario from the AP Physics Workbook, focusing on unit five, momentum. It describes an explosion at the center of mass, affecting a one-kilogram block moving to the left and a four-kilogram block to the right. The first part of the problem involves calculating the time it takes for each block to hit a block, using kinematics equations and noting the absence of horizontal acceleration. The key concept here is the conservation of momentum, which is used to determine the final velocity of the four-kilogram block after the explosion. The paragraph emphasizes the importance of understanding momentum conservation and its application in solving problems involving motion and forces.

05:01
πŸ“ Center of Mass Shift and Deceleration Calculation

The second paragraph delves into the concept of the center of mass during and after an explosion. It explains how the center of mass changes as the distance between the two masses increases. The paragraph also provides a formula for calculating the center of mass, emphasizing its dependency on the masses and distances of the objects involved. Furthermore, it discusses the system's experience of a net force during the explosion, leading to a shift in the center of mass. The summary also touches on the calculation of deceleration when the blocks encounter a rough surface, introducing the concept of frictional force and its impact on the motion of the objects. This section aims to clarify the principles of center of mass and the effects of external forces on it.

Mindmap
Keywords
πŸ’‘Momentum
Momentum is a fundamental concept in physics that represents the quantity of motion of an object, defined as the product of an object's mass and velocity. In the video, momentum is central to understanding the behavior of the 1 kg and 4 kg blocks after the explosion. The conservation of momentum principle is used to calculate the final velocities of the blocks, which is crucial for solving the problems presented in the tutorial.
πŸ’‘Center of Mass
The center of mass is the point at which the mass of an object, or a system of objects, is concentrated for the purpose of understanding its motion. In the context of the video, the center of mass changes as the 1 kg and 4 kg blocks move apart after the explosion. The tutorial explains how to calculate the center of mass and how it shifts during the motion of the blocks, which is essential for understanding the dynamics of the system.
πŸ’‘Kinematics Equations
Kinematics equations are mathematical relationships that describe the motion of an object without considering the forces that cause the motion. In the video, these equations are used to calculate the time it takes for the 1 kg and 4 kg blocks to hit a block and to determine their velocities. The equations are essential tools for solving problems related to motion and are applied multiple times throughout the tutorial.
πŸ’‘Explosive Reaction
An explosive reaction, as mentioned in the video, refers to the event where an explosion occurs in the center of the two blocks, causing them to move apart. This event is significant as it initiates the motion of the blocks and is the starting point for the application of the conservation of momentum and kinematics equations to analyze their subsequent movement.
πŸ’‘Conservation of Momentum
The law of conservation of momentum states that the total momentum of a closed system remains constant if no external forces act on it. In the video, this principle is used to calculate the final velocities of the 1 kg and 4 kg blocks after the explosion. The conservation of momentum is a key concept that helps in understanding how the system's motion changes over time.
πŸ’‘Deceleration
Deceleration is the rate at which an object's velocity decreases. In the video, deceleration is calculated for both the 1 kg and 4 kg blocks as they slide on the rough surface after hitting it. The concept is crucial for understanding how the frictional force acting on the blocks causes them to slow down and eventually come to a stop.
πŸ’‘Friction
Friction is a force that opposes the relative motion or tendency of such motion of two surfaces in contact. In the video, friction plays a significant role when the blocks hit the rough surface, causing them to experience a deceleration due to the frictional force. The tutorial explains how to calculate this force and its effect on the motion of the blocks.
πŸ’‘Acceleration
Acceleration is the rate of change of velocity of an object with respect to time. In the context of the video, acceleration is calculated for the blocks as they slide on the rough surface, which helps determine how quickly they slow down. The concept of acceleration is essential for understanding the dynamics of the blocks' motion and how they come to rest.
πŸ’‘Time
Time is a fundamental aspect of the video as it is used to calculate the duration of the blocks' motion. The tutorial shows how to determine the time it takes for the 1 kg and 4 kg blocks to hit the block and come to a stop. Time is a key factor in understanding the kinematics of the system and is calculated using the kinematics equations.
πŸ’‘Velocity
Velocity is a vector quantity that describes the speed of an object in a specific direction. In the video, the initial and final velocities of the 1 kg and 4 kg blocks are crucial for solving the problems. The tutorial explains how to calculate these velocities using the conservation of momentum and kinematics equations, which is essential for understanding the motion of the blocks.
πŸ’‘Net External Force
A net external force is the vector sum of all external forces acting on an object or system. In the video, the absence of a net external force before the explosion means that the system's momentum is conserved. After the explosion, the net external force due to friction comes into play, affecting the motion of the blocks and causing changes in their momentum and center of mass.
Highlights

Exploration of momentum conservation in physics

Description of an explosion affecting a one kilogram and a four kilogram block

Use of kinematics equations for horizontal motion analysis

Negative velocity indicating leftward motion

Calculation of time for the one kilogram block to hit a surface

Utilization of momentum conservation for unknown final velocities

Determination of the four kilogram block's final velocity as positive 10

Friction force calculation and its impact on deceleration

Derivation of acceleration due to friction as 5 m/s^2

Calculation of time for the one kilogram block to come to rest

Total time calculation for the four kilogram block to stop after sliding

Explanation of the center of mass concept and its changes during motion

Discussion on the center of mass being at equilibrium with no net external force

Analysis of the center of mass increase due to the distance between masses increasing

Formula for calculating the center of mass using mass and distance

Clarification on how the center of mass changes as objects move apart

Transcripts

Browse More Related Video

2021 AP Physics 1 Free Response #3 (First Administration)

AP Physics C: Momentum, Impulse, Collisions & Center of Mass Review (Mechanics)

2019 #1 Free Response Question - AP Physics 1 - Exam Solution

AP Physics Workbook 5.J Explosions

AP Physics Workbook 5.A Center of Mass

Angular momentum | Moments, torque, and angular momentum | Physics | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Physics EducationMomentum AnalysisCenter of MassKinematics EquationsConservation of MomentumExplosive ScenariosProblem SolvingMechanics ConceptsFrictional ForcesLinear Motion