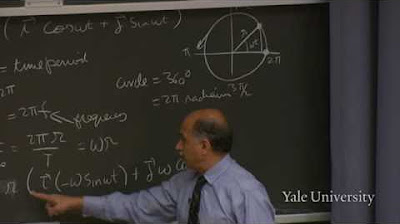3. Newton's Laws of Motion
TLDRIn this lecture, Professor Ramamurti Shankar discusses the fundamentals of motion in more than one dimension, emphasizing the use of vectors for describing movement. He delves into the concept of the position vector and its components, as well as the transformation of components when using different axes. The professor also explores the importance of understanding Newton's laws, particularly the Law of Inertia and the relationship between force, mass, and acceleration. Through examples of particle motion and the use of springs in zero gravity, he illustrates how to measure mass and acceleration, highlighting the practical application of these concepts in physics.
Takeaways
- 📚 The primary concept discussed is the handling of motion in more than one dimension, with a focus on two-dimensional motion and the use of vectors for description.
- 🔄 Vectors are essential for describing objects in two dimensions or more, with the position vector being the most significant, having x and y components that vary with time.
- 🌟 The components of a vector are not invariant; they change with the perspective or the chosen set of axes, highlighting that the vector has a 'life of its own' independent of its representation.
- 📐 The transformation of vector components between different reference frames is governed by a law involving the relationship between the unit vectors in each frame.
- 🔄 The example of a particle moving in a circular path in the xy-plane illustrates the concepts of centripetal acceleration and angular velocity, with the acceleration directed towards the center of the circle.
- 🚀 Newton's laws are introduced as the foundation for understanding and explaining a vast array of physical phenomena, with an emphasis on their subtlety and depth beyond simple application.
- 🛑 The Law of Inertia, Newton's first law, states that an object will remain at rest or in uniform motion in a straight line unless acted upon by an external force.
- 📈 The second law, F=ma, relates force, mass, and acceleration, with the force measured in Newtons (N) and the mass in kilograms (kg).
- 🔄 The third law discusses action and reaction, stating that for every action, there is an equal and opposite reaction, highlighting the mutual nature of forces between bodies.
- 🤹♂️ The process of measuring mass and force involves conventions and comparisons, such as using a spring to determine the mass of an object by comparing its acceleration to a known mass.
- 🌌 The concepts discussed are not only applicable to Earth but also to inertial frames of reference, such as those in free space, where the true nature of motion and forces can be observed without the interference of gravity or other external forces.
Q & A
How does the concept of vectors apply to motion in more than one dimension?
-In multidimensional motion, vectors are essential for describing the position, velocity, and acceleration of an object. The position vector, for example, has components in the x and y directions that can vary with time. The unit vectors I and J represent the directions of the x and y axes, respectively. Vectors can be manipulated either as arrows or as pairs of numbers (components), and their components change with the choice of axes.
What is the significance of the position vector in describing motion?
-The position vector is crucial in describing the location of an object in two-dimensional or multidimensional space. It has components along the axes (x and y in 2D), which can change with time, indicating the object's movement. The position vector provides a mathematical representation of where the object is at any given moment.
How does the choice of axes affect the components of a vector?
-The components of a vector change depending on the set of axes chosen. If the axes are not in the traditional orthogonal directions (x and y), but in an oblique direction, the unit vectors are different (I' and J'), and so are the components of the vector. This demonstrates that the components are not invariant; they depend on the reference frame chosen.
What is the Law of Inertia and why is it significant?
-The Law of Inertia, the first of Newton's laws, states that an object at rest will stay at rest, and an object in motion will stay in motion with a constant velocity, unless acted upon by a net external force. This law is significant because it challenges the Aristotelian view that a force is required to maintain motion, showing instead that a constant velocity can be maintained without any force.
How does the concept of an inertial observer relate to Newton's laws?
-An inertial observer is one for whom Newton's laws of motion hold true. In the context of the Law of Inertia, an inertial observer is at rest or moving at a constant velocity in a straight line. If one inertial observer measures a body to be at rest or in motion, any other observer moving at a constant velocity relative to the first will also measure the body to be at rest or in motion, thus validating the Law of Inertia across different frames of reference.
What is the relationship between the time period, frequency, and angular velocity?
-The time period (T) is the duration for one complete cycle of motion, the frequency (f) is the number of cycles per unit time, and the angular velocity (ω) is the rate of change of the angle per unit time. They are related by the equations T = 1/f and ω = 2πf. The angular velocity is the product of 2π and the frequency, which gives the number of radians per second through which an object rotates in one second.
How is centripetal acceleration described mathematically and what does it represent?
-Centripetal acceleration is described mathematically as a = v^2 / r, where 'a' is the centripetal acceleration, 'v' is the linear speed of the object, and 'r' is the radius of the circular path. It represents the acceleration directed towards the center of the circle that an object experiences when it is moving in a circular path at a constant speed.
What is the significance of the unit vector e_r in physics?
-The unit vector e_r is significant in physics as it points radially outward from the center of a circular path at each point along the path. It has a length of one and is always directed away from the center, making it a convenient tool for describing radial forces and motions, such as gravitational and Coulomb interactions.
How does the Law of Inertia apply to an object on an accelerating airplane?
-The Law of Inertia does not apply to an object on an accelerating airplane in the same way it applies to an object in a stable, inertial frame of reference. On an accelerating airplane, such as during takeoff, an object that appears to be at rest relative to the airplane will slide backward due to the airplane's acceleration, indicating that the airplane is not an inertial reference frame at that moment.
What is the role of the force constant 'k' in describing the behavior of a spring?
-The force constant 'k' is a measure of the stiffness of a spring. It describes the amount of force exerted by the spring for a given amount of deformation (stretching or compression). The relationship between the force 'F' exerted by the spring and the displacement 'x' from its equilibrium position is given by Hooke's Law, F = -kx, where the negative sign indicates that the force exerted by the spring is always opposite in direction to the displacement.
Outlines
📚 Introduction to Vectors and Motion in Multi-Dimensional Space
Professor Shankar begins the lecture by recapping the previous session's content on handling motion in more than one dimension, specifically focusing on two-dimensional motion. He emphasizes the use of vectors to describe objects in multi-dimensional spaces and introduces the concept of the position vector. The professor also discusses the importance of unit vectors and the transformation of vector components when using different axes. The lecture touches on the oblique direction of axes and the resulting change in unit vectors, highlighting the invariant nature of vectors themselves. The professor concludes the summary by discussing the homework problems related to the transformation of vector components.
🌀 Understanding Angular Velocity and Circular Motion
The paragraph delves into the concept of angular velocity (ω) and its relationship with the time period of circular motion. The professor explains that ω is a simple quantity related to the frequency of circular motion, multiplied by 2π to account for the rate of angular change. The discussion then moves to the acceleration of a particle moving in a circular path, with the professor demonstrating that the acceleration is directed towards the center of the circle and has a magnitude proportional to the square of ω and the radius of the circle. The concept of centripetal acceleration is introduced, and the professor emphasizes the importance of understanding this for any particle in circular motion. The paragraph concludes with a brief mention of projectile motion and the application of Newton's laws in future lectures.
🚀 Newton's Laws: Inertia and the Nature of Forces
In this section, Professor Shankar introduces Newton's laws, emphasizing their subtlety and the deep understanding required to apply them effectively. He discusses the first law, the Law of Inertia, which states that an object will remain at rest or in uniform motion unless acted upon by an external force. The professor highlights the non-intuitive aspect of this law, which is the idea that a force is not needed for an object to maintain a constant velocity. He also points out that Newton's laws are not universally applicable to every observer, but only to 'inertial observers' who are not accelerating relative to the rest of the universe. The lecture touches on the importance of recognizing the nature of the forces acting on a body and the need to identify these forces correctly to solve mechanical problems.
📈 Measuring Mass and Force: The Role of Conventions and Experiments
The professor discusses the challenges in measuring mass and force, using thought experiments in the context of outer space to illustrate the points. He emphasizes that mass is a measure of a body's resistance to acceleration and is independent of gravitational pull. The lecture introduces the concept of a spring as a tool for measuring mass, where the acceleration produced by the spring on a known mass can be used to infer the mass of an unknown object. The professor also discusses the force exerted by a spring, which is characterized by its force constant (k), and how this force is related to the extension of the spring. The discussion concludes with the importance of understanding how physical quantities are measured and defined, and the distinction between inertial and gravitational mass.
🔧 Newton's Laws Applied to Springs and Connected Bodies
In this part of the lecture, Professor Shankar applies Newton's laws to scenarios involving springs and connected bodies. He explains how the force exerted by a spring can be determined by measuring the acceleration of a known mass. The professor also discusses the concept of action and reaction forces, as described by Newton's third law, and how these forces manifest in systems of connected bodies. The lecture provides a detailed explanation of how to use free-body diagrams to analyze the forces acting on individual bodies and solve for unknowns like acceleration and tension in the rope. The professor concludes with a practical example of how the apparent weight changes in an elevator depending on its acceleration, demonstrating the application of Newton's laws in everyday situations.
Mindmap
Keywords
💡motion in more than one dimension
💡vectors
💡position vector
💡unit vectors
💡components of a vector
💡reference frame
💡acceleration
💡centripetal acceleration
💡Newton's laws of motion
💡inertia
💡force
Highlights
Introduction to handling motion in more than one dimension using two dimensions as the standard way to explain it.
The importance of vectors in describing motion in two or more dimensions, with the position vector being the most important vector.
The concept of unit vectors in the x and y directions and how they can be represented as an arrow or a pair of numbers (x and y).
The rule for adding two vectors either by thinking of them as arrows or by adding their x and y components.
The ability to choose a different set of axes, leading to different unit vectors and components, emphasizing that vector components are not invariant.
The law of transformation of vector components between different reference frames and how to solve for it using simultaneous equations.
The example of a particle moving in the xy plane, illustrating the relationship between vector components and physical motion.
The concept of angular velocity (ω) and its relationship with the time period and frequency of circular motion.
The derivation of centripetal acceleration and its significance in understanding circular motion.
The introduction of the radial unit vector (e_r) and its importance in describing radial motion and gravitational interactions.
The transition from discussing motion in two dimensions to the central topic of Newton's laws.
The explanation of Newton's first law, the Law of Inertia, and its implications for understanding motion without external forces.
The concept of inertial observers and how Newton's laws apply to them, with examples from everyday experiences like an airplane takeoff.
The discussion on the nature of constant velocity and the non-obvious nature of its relationship with forces, challenging common intuitions.
The introduction of Newton's second law, F=ma, and the importance of understanding the relationship between force, mass, and acceleration.
The explanation of the units of measurement for force (Newton) and the process of measuring force and mass using a spring in outer space.
The distinction between the universal nature of Newton's second law (F=ma) and the specific force characteristics of a spring (F=-kx).
The importance of understanding how physical quantities are measured and defined, emphasizing the difference between symbolic representation and physical measurement.
The discussion on the nature of mass as an inherent property of an object that resists acceleration in response to a force.
The explanation of how to measure the mass of an object using a spring and the concept of comparing accelerations.
The introduction of Newton's third law and the concept of action and reaction forces, emphasizing the importance of identifying all forces acting on a body.
The advice on not adding non-existent forces and focusing on tangible material causes for forces, with a focus on direct contact or gravity.
The practical application of Newtonian mechanics in solving problems involving forces, mass, and acceleration, using free-body diagrams and algebraic methods.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: