Static Friction and Kinetic Friction Physics Problems With Free Body Diagrams
TLDRThe video script discusses the concepts of static and kinetic friction, using examples of a box on a carpet to illustrate their differences. It explains that static friction is the force preventing an object from moving, while kinetic friction impedes motion once the object is in motion. The script provides equations for calculating these forces and demonstrates how the maximum static friction is an inequality, whereas kinetic friction is a fixed value. It also covers how to determine the minimum force required to initiate movement and how to calculate the acceleration of an object when it is sliding, using the coefficients of friction and the normal force.
Takeaways
- 📌 Static friction is the force that prevents an object from moving when a force is initially applied, while kinetic friction is the force that opposes the motion of an object once it has started sliding.
- 📌 The maximum static frictional force can be calculated using the equation fs ≤ μs * N, where fs is the static frictional force, μs is the coefficient of static friction, and N is the normal force.
- 📌 Kinetic frictional force is calculated with fk = μk * N, where fk is the kinetic frictional force and μk is the coefficient of kinetic friction.
- 📌 The coefficients of static and kinetic friction are different, with μs typically being greater than μk.
- 📌 The normal force (N) on a horizontal surface is equal to the weight force (mg) of the object, where m is the mass and g is the acceleration due to gravity.
- 📌 Static friction matches the applied force until it reaches its maximum value, after which the object begins to slide and kinetic friction takes over.
- 📌 To initiate movement, the applied force must exceed the maximum static frictional force, which is the threshold for the object to start sliding.
- 📌 Once an object is in motion, the net force acting on it is the difference between the applied force and the kinetic frictional force (F - fk).
- 📌 The acceleration of an object can be calculated using Newton's second law (F = ma), where F is the net force, m is the mass, and a is the acceleration.
- 📌 When an object is subjected to forces in multiple directions, it's important to consider the components of those forces and how they affect the normal force.
- 📌 The horizontal acceleration of an object can be determined by considering the forces acting on it in the direction of motion and using the appropriate equations to solve for acceleration.
Q & A
What is the main difference between static friction and kinetic friction?
-Static friction is the force that prevents an object from starting to move when a force is applied to it, while kinetic friction is the force that opposes the motion of an object when it is already sliding.
How is the static frictional force calculated?
-The static frictional force is calculated using the formula fs ≤ μs * N, where fs is the static frictional force, μs is the coefficient of static friction, and N is the normal force.
What is the formula for calculating kinetic friction?
-Kinetic friction is calculated using the formula fk = μk * N, where fk is the kinetic frictional force, μk is the coefficient of kinetic friction, and N is the normal force.
What happens when the applied force exceeds the maximum static frictional force?
-When the applied force exceeds the maximum static frictional force, the object begins to slide, and kinetic friction takes over as the force opposing the motion.
What is the relationship between the coefficients of static and kinetic friction?
-Typically, the coefficient of static friction (μs) is greater than the coefficient of kinetic friction (μk), meaning it takes more force to initiate movement than to maintain it once started.
How do you determine the normal force on a horizontal surface?
-On a horizontal surface, the normal force is equal to the weight force (N = mg), where m is the mass of the object and g is the acceleration due to gravity.
What is the minimum horizontal force required to start sliding a 15 kg box on a surface with a static friction coefficient of 0.35?
-The minimum horizontal force required is 51.45 newtons, calculated using fs = μs * N = 0.35 * (15 kg * 9.8 m/s^2).
If a 65 newton force is needed to start an 8 kg box sliding, what is the coefficient of static friction?
-The coefficient of static friction is 0.829, calculated using μs = F / (m * g) = 65 N / (8 kg * 9.8 m/s^2).
What is the acceleration of a system when a 90 newton force is applied to a 15 kg box with a static friction coefficient of 0.35?
-The acceleration is 4.04 m/s^2, calculated using a net force of (90 N - fk) / m, where fk = μk * N = 0.20 * (15 kg * 9.8 m/s^2) and the initial normal force is the weight of the box (mg).
How does the normal force change when a box is being lifted or pressed down?
-When a box is being lifted, the normal force decreases because the upward force partially supports the weight of the box. Conversely, when a box is pressed down, the normal force increases because the surface must support the additional downward force applied to the box.
What is the horizontal acceleration of a 30 kg box when a 150 newton force is applied, with a kinetic friction coefficient of 0.25?
-The horizontal acceleration is 2.505 m/s^2, calculated using the net force (Fx - fk) / m, where Fx = F * cos(θ) and fk = μk * N, with the normal force adjusted for the y-component of the applied force.
Outlines
🚪 Introduction to Static and Kinetic Friction
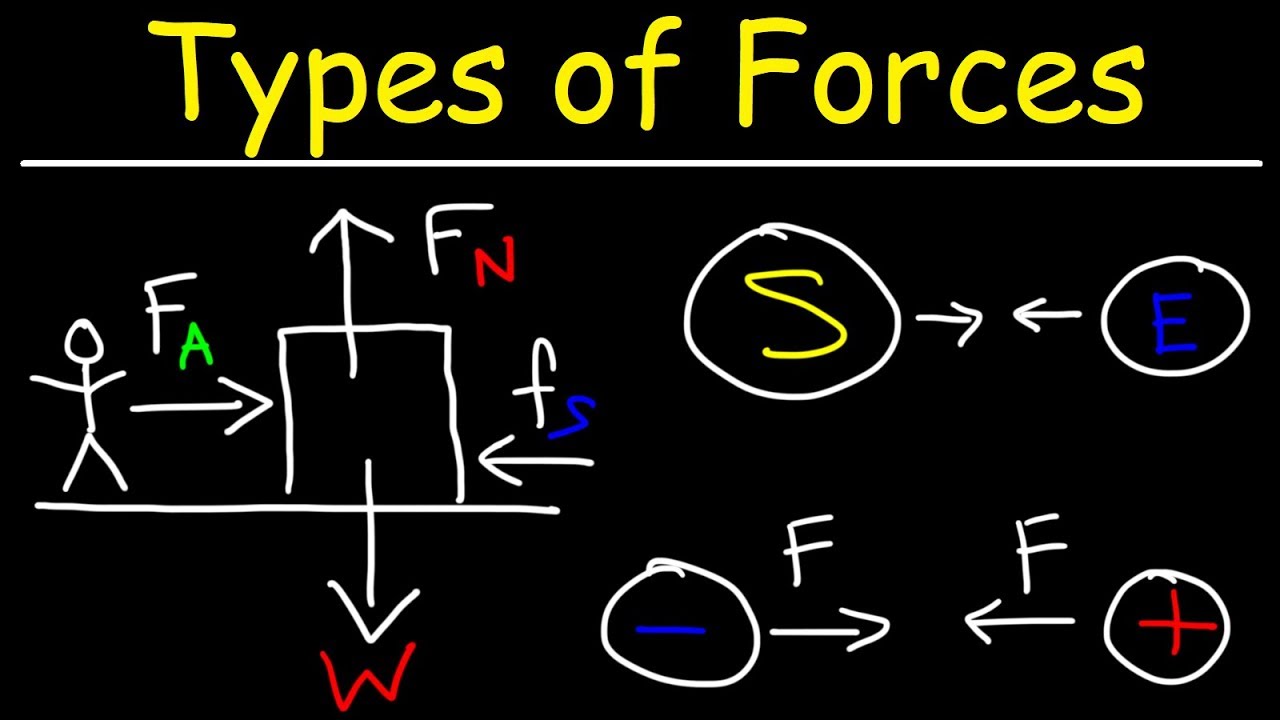
This paragraph introduces the concepts of static and kinetic friction using the example of pushing a box on a carpeted floor. It explains that static friction is the force preventing the box from initially moving, while kinetic friction is the force that opposes the box's motion once it starts sliding. The difference between static (not moving) and kinetic (motion-related) friction is highlighted. Equations for both types of friction are presented: static friction is ≤ μs * N (with μs being the coefficient of static friction and N the normal force), and kinetic friction is μk * N (with μk being the coefficient of kinetic friction). The example of a 5 kg box is used to calculate these forces with given coefficients and the normal force.
🔄 Interaction of Applied Force and Friction
This paragraph discusses the interaction between the applied force to move the box and the frictional forces at play. It clarifies that static and kinetic friction cannot exist simultaneously; static friction is present when the box is not sliding, and kinetic friction takes over once the box starts sliding. The concept is illustrated with a table showing the relationship between the applied force, static and kinetic frictional forces, and the net force. The discussion includes scenarios where the applied force is less than, equal to, or greater than the maximum static frictional force, explaining the box's response in each case.
📈 Calculating Minimum Force and Acceleration
This paragraph focuses on calculating the minimum horizontal force required to initiate sliding (threshold of static friction) and the subsequent acceleration of the box once it starts sliding. The problem-solving approach is demonstrated with a 15 kg box on a horizontal surface, using the coefficient of static friction. The calculation involves determining the maximum static frictional force and the net force needed to overcome it. The acceleration is then calculated by applying Newton's second law once the box is sliding and is subject to kinetic friction.
🔄 Determining Friction Coefficients
The paragraph involves two problems that demonstrate how to calculate the coefficients of static and kinetic friction. The first problem gives the force required to initiate movement and calculates the static friction coefficient using the formula. The second problem provides the acceleration of a moving box and asks for the kinetic friction coefficient. Both problems use the principles of net force and Newton's second law to solve for the unknown coefficients, highlighting the relationship between applied force, frictional force, mass, and acceleration.
🌐 Factors Affecting Normal Force and Acceleration
This paragraph delves into the factors that affect the normal force, particularly when a box is subjected to forces that are not perpendicular to the surface. It explains how pressing down on or trying to lift a box changes the normal force compared to when the box is simply resting on a horizontal surface. The example involves a 30 kg box being pulled with a force of 150 N at an angle, and the challenge is to find the box's horizontal acceleration with a given kinetic friction coefficient. The solution requires understanding that the normal force is not equal to the weight of the box in this scenario and involves calculating the normal force based on the vertical component of the applied force and the weight of the box. The horizontal acceleration is then found using the net force in the x-direction and Newton's second law.
Mindmap
Keywords
💡Static Friction
💡Kinetic Friction
💡Coefficient of Friction
💡Normal Force
💡Applied Force
💡Net Force
💡Acceleration
💡Weight Force
💡Newton's Second Law
💡Threshold Value
Highlights
Static friction is the force that prevents an object from initially moving, while kinetic friction is the force that opposes motion when the object is already sliding.
The maximum static frictional force can be calculated using the equation fs ≤ μs * N, where fs is the static frictional force, μs is the coefficient of static friction, and N is the normal force.
Kinetic friction is represented by a fixed value calculated with fk = μk * N, where fk is the kinetic frictional force and μk is the coefficient of kinetic friction.
A box on a horizontal surface exerts a downward weight force, and the normal force exerted by the surface on the box is perpendicular to the surface and equals the weight force (N = mg).
The coefficient of static friction (μs) is typically greater than the coefficient of kinetic friction (μk), and examples show that μk is not greater than μs.
To calculate the frictional forces, given a 5 kg box with a static friction coefficient of 0.4 and a kinetic friction coefficient of 0.2, the normal force is 5 kg * 9.8 m/s^2 = 49 N.
The kinetic frictional force (fk) for the 5 kg box is 0.2 * 49 N = 9.8 N, and the maximum static frictional force (fs) is 0.4 * 49 N = 19.6 N.
Static friction matches the applied force until it reaches its maximum value; it does not simply default to the maximum static frictional force.
An applied force of 20 N on a 5 kg box with a static frictional force of 19.6 N will cause the box to slide, as the net force becomes 20 N - 9.8 N = 10.2 N.
For a 15 kg box, the minimum horizontal force required to initiate sliding is calculated by setting the applied force (F) equal to the maximum static frictional force (fs), which is μs * mg.
The threshold force for a 15 kg box to begin sliding with a static friction coefficient of 0.35 is 51.45 N, which is just above the maximum static frictional force.
When the box is pushed with a force of 90 N on a horizontal surface, the acceleration of the system can be calculated using Newton's second law and considering kinetic friction.
The acceleration of the system when pushing the 15 kg box with a force of 90 N is 4.04 m/s^2, considering the kinetic frictional force.
To find the coefficient of static friction for an 8 kg box that requires a force of 65 N to start moving, the formula fs = μs * N is used, resulting in a coefficient of 0.829.
The coefficient of kinetic friction for the 8 kg box, moving with an acceleration of 1.4 m/s^2, is calculated to be 0.686, using the net force and the mass of the box.
When a 30 kg box is pulled with a force of 150 N and the coefficient of kinetic friction is 0.25, the horizontal acceleration can be determined by considering the components of the applied force and the normal force.
The horizontal acceleration of the 30 kg box, given a 150 N pulling force and a kinetic friction coefficient of 0.25, is calculated to be 2.505 m/s^2, taking into account the normal force and the force components.
Understanding the relationship between the normal force and the weight force is crucial when dealing with inclined planes or forces that press down or lift up an object.
The normal force changes depending on whether an object is being pressed down upon or lifted; it increases with downward pressure and decreases with upward forces.
When calculating the frictional forces and acceleration, it is important to consider the direction of the applied forces and the components of those forces.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: