Variance: Why n-1? Intuitive explanation of concept and proof (Bessel‘s correction)
TLDRThe video script delves into the reason behind multiple formulas for empirical variance, focusing on the distinction between using 'n' and 'n-1' in the denominator. It explains the concept of Bessel's correction, which addresses the bias introduced when estimating the population variance using sample data. The script provides an intuitive understanding of why the correction factor is 'n-1' rather than any other value, emphasizing its importance in inferential statistics to yield an unbiased estimator of variance.
Takeaways
- 🧠 The existence of multiple formulas for empirical variance is due to different statistical contexts and the need for accurate estimation of population variance from samples.
- 🔍 The standard formula for variance uses the sample size (n) in the denominator, while the inferential statistics version uses n-1, known as Bessel's correction.
- 📉 Bessel's correction addresses the bias introduced when estimating the population mean from a sample, leading to an accurate estimation of the population variance.
- 🤔 The counterintuitive aspect of n-1 is that it corrects the variance formula not because of the sample mean itself, but due to the relationship between the sample mean and the number of data points.
- 📊 Empirical variance measures the spread of data points; a larger spread results in higher variance, calculated by squaring the distances from the mean and averaging them.
- 🌟 Using n-1 in the denominator instead of n provides an unbiased estimator for the population variance when only a sample is available, and the population mean is unknown.
- 🏆 The two scenarios where using n in the denominator is appropriate are when you have access to the entire population or when you know both the population mean and have a sample.
- 🧩 The concept of degrees of freedom in statistics is related to Bessel's correction, but it doesn't fully explain the rationale behind the correction.
- 🔧 Bessel's correction can be intuitively understood by examining the properties of the variance formula and the behavior of sample means in relation to population means.
- 📈 The distribution of sample means is symmetric and centered around the population mean, with more extreme means being less likely than those closer to the population mean.
- 🔄 The variance formula's bias can be corrected by mathematically adjusting for the difference between the expected values of the sample and population variances, resulting in n-1 as the critical factor.
Q & A
Why are there multiple formulas for calculating empirical variance?
-Multiple formulas exist because one formula is used for descriptive statistics where the population mean is known, and another for inferential statistics where the population mean is estimated using the sample mean. The latter requires Bessel's correction (n-1 in the denominator) to account for the estimation of the mean from the sample data.
What is Bessel's correction and why is it used?
-Bessel's correction is the adjustment made to the denominator of the variance formula when estimating the population variance from a sample. It is used to correct the bias that occurs because the sample mean is used as an estimate for the population mean, which tends to underestimate the true variance.
How does the sample mean affect the calculation of variance?
-When the sample mean is used in place of the population mean to calculate variance, it tends to minimize the result within that sample, leading to an underestimation of the true population variance. This is because sample data points are generally closer to the sample mean than to the population mean.
What are the two scenarios where you can use the variance formula with n in the denominator?
-You can use the formula with n in the denominator when you have access to the entire population data, allowing you to calculate the population mean directly, or when you have a sample and also know the population mean, which is a rare scenario.
Why does using n instead of n-1 in the denominator when estimating variance lead to an underestimated variance?
-Using n instead of n-1 in the denominator leads to an underestimated variance because the sample mean is used as an estimate for the population mean, which inherently biases the calculation by making the sample data points appear closer to the mean than they actually are in the context of the entire population.
What is the intuitive reasoning behind using n-1 in the denominator for variance estimation?
-The intuitive reasoning is that when estimating the population variance from a sample, the sample mean is used as an estimate for the population mean. This introduces bias because the sample mean tends to minimize the sum of squared differences within the sample. By using n-1 instead of n, we correct for this bias, making the estimator unbiased.
How does the variance formula with squared pairwise differences help explain Bessel's correction?
-The variance formula with squared pairwise differences shows that when a sample is taken from the population, the number of zero differences (data points being the same as themselves) is proportionally higher in the sample than in the population. This leads to an underestimation of the variance, and dividing by n-1 instead of n corrects for this by excluding the 'self-differences' from the calculation.
What is the relationship between the variance of the sample mean and Bessel's correction?
-The expected difference between the true population variance and the biased sample variance (using n in the denominator) is equal to the variance of the sample mean. Bessel's correction is derived from this relationship, showing that dividing the biased estimator by n/(n-1) yields an unbiased estimator of the population variance.
Why is the correction factor for the variance formula n-1 divided by n?
-The correction factor n-1 divided by n accounts for the fact that in a sample, each data point has n-1 other points to compare with, rather than n. This adjustment corrects the bias introduced by using the sample mean instead of the population mean in the variance calculation.
How does the concept of degrees of freedom relate to Bessel's correction?
-The degrees of freedom in this context refer to the number of independent observations that can vary freely when calculating the sample mean and variance. When estimating the mean from the sample, one degree of freedom is lost because the sum of the sample values is fixed. Thus, n-1 is used in the denominator of the variance formula to account for this loss of a degree of freedom.
What is the impact of Bessel's correction on small sample sizes?
-Bessel's correction has a more significant impact on small sample sizes because the bias introduced by using the sample mean is more pronounced when the sample is smaller. The correction helps to ensure that the variance is more accurately estimated in these cases.
Outlines
🔍 Introduction to Empirical Variance and Bessel's Correction
This paragraph introduces the concept of empirical variance and the existence of multiple formulas to calculate it. It highlights the common confusion between using 'n' and 'n-1' in the denominator and teases an in-depth explanation of Bessel's correction. The importance of understanding this concept is emphasized due to its counterintuitive nature and the lack of comprehensive explanations often found in traditional teachings.
📈 Understanding Sample Mean and Population Mean in Variance Calculation
This paragraph delves into the reasons behind using 'n' when the population mean is known and 'n-1' when it's estimated from a sample. It explains that the use of 'n-1' is related to the need to account for the additional estimation of the population mean from the sample. The paragraph also clarifies the terms population value and sample value, and the conditions under which each formula should be used. The potential issue of underestimating variance when using the sample mean is introduced.
🧠 Exploring the Bias in Variance Estimation
This paragraph discusses the concept of bias in the context of variance estimation, specifically when using the sample mean. It explains that the sample mean has a special property within the variance formula that tends to minimize the result, leading to an underestimation of the true variance. The paragraph uses examples and a graphical representation to illustrate how the sample mean can differ from the population mean, and how this difference affects the accuracy of variance estimation.
🤔 Analyzing the Relationship Between Sample Mean and Variance
The paragraph examines why sample data points tend to be closer to the sample mean than to the population mean, which introduces bias in variance estimation. It uses different values and examples to show how plugging in values other than the mean results in a larger variance calculation. The paragraph also introduces a graphical representation of the variance formula, highlighting the parabola formed by different values plugged into the formula, with the mean corresponding to the minimum value.
📊 Correcting Bias with Bessel's Correction
This paragraph provides a detailed explanation of Bessel's correction, demonstrating why using 'n-1' instead of 'n' in the denominator of the variance formula eliminates the bias introduced by estimating the population mean from a sample. It presents a mathematical approach to formalize the bias and shows how the correction factor is derived. The paragraph emphasizes that the correction is not about ignoring one data point, but rather about adjusting the estimator to account for the variance of the sample mean.
🔬 Alternative Explanation Using Pairwise Differences
The paragraph offers an alternative intuitive explanation for Bessel's correction by introducing the concept of pairwise differences between data points as a method to calculate variance. It explains that this approach avoids the complexity of algebraic formulas and provides a clear visual representation of the bias issue. The explanation highlights how the zeros on the diagonal of the pairwise differences matrix contribute to the bias and how dividing by 'n-1' corrects this by excluding the 'self-differences' from the calculation.
🎓 Conclusion and Final Thoughts on Bessel's Correction
In conclusion, the paragraph wraps up the discussion on Bessel's correction by reiterating its purpose in eliminating bias when estimating the population variance from a sample. It clarifies that the correction is not about ignoring a data point but rather adjusting for the overrepresentation of zeros in the sample's pairwise differences. The paragraph also notes the impact of the correction on small samples and mentions that the unbiasedness is not always the primary concern, suggesting that different corrections may be suitable for different applications.
Mindmap
Keywords
💡Empirical Variance
💡Bessel's Correction
💡Degrees of Freedom
💡Sample Mean (x̄)
💡Population Mean (μ)
💡Unbiased Estimator
💡Sum of Squares
💡Variance Formula
💡Statistical Bias
💡Inferential Statistics
Highlights
Multiple formulas for empirical variance exist due to different statistical contexts and requirements.
The version with n-1 in the denominator is introduced in inferential statistics when estimating the population variance from a sample.
Bessel's correction is used to adjust the variance formula when using a sample mean instead of the population mean.
Using n instead of n-1 in the denominator when estimating variance from a sample can lead to an underestimation of the true variance.
The sample mean is an unbiased estimator for the population mean, meaning that over many samples, the average of these means will equal the population mean.
The distribution of sample means is symmetric and centered around the population mean, becoming narrower with increasing sample size.
The variance formula with n in the denominator and the sample mean is biased because the sample mean minimizes the sum of squared differences within the sample.
The expected difference between the true variance and the biased estimate is equal to the variance of the sample mean.
Bessel's correction can be derived by comparing the expected values of the biased and unbiased variance formulas, leading to n-1 in the denominator.
An alternative variance formula using pairwise differences provides an intuitive understanding of Bessel's correction without complex algebra.
In the pairwise differences approach, the sample case has a higher ratio of zero differences compared to the full population, leading to an underestimation of variance.
The correction factor n/(n-1) adjusts the biased variance estimate by accounting for the overrepresentation of zero differences in the sample.
The n-1 correction is most impactful for small sample sizes and is a standard method to achieve unbiased estimation of population variance from samples.
Unbiasedness is not always the primary concern in statistical applications, and different corrections may be used based on the specific context.
The square root of variance, known as the standard deviation, is not rendered unbiased by Bessel's correction and may require separate consideration.
The transcript provides a comprehensive explanation of the rationale behind Bessel's correction and its significance in statistical analysis.
The transcript clarifies common misconceptions about Bessel's correction and offers a clear, step-by-step breakdown of its derivation and application.
Transcripts
Browse More Related Video
Why We Divide by N-1 in the Sample Variance (Standard Deviation) Formula | The Bessel's Correction
The Sample Variance: Why Divide by n-1?
Unbiased Estimators (Why n-1 ???) : Data Science Basics

Review and intuition why we divide by n-1 for the unbiased sample | Khan Academy
Dividing By n-1 Explained
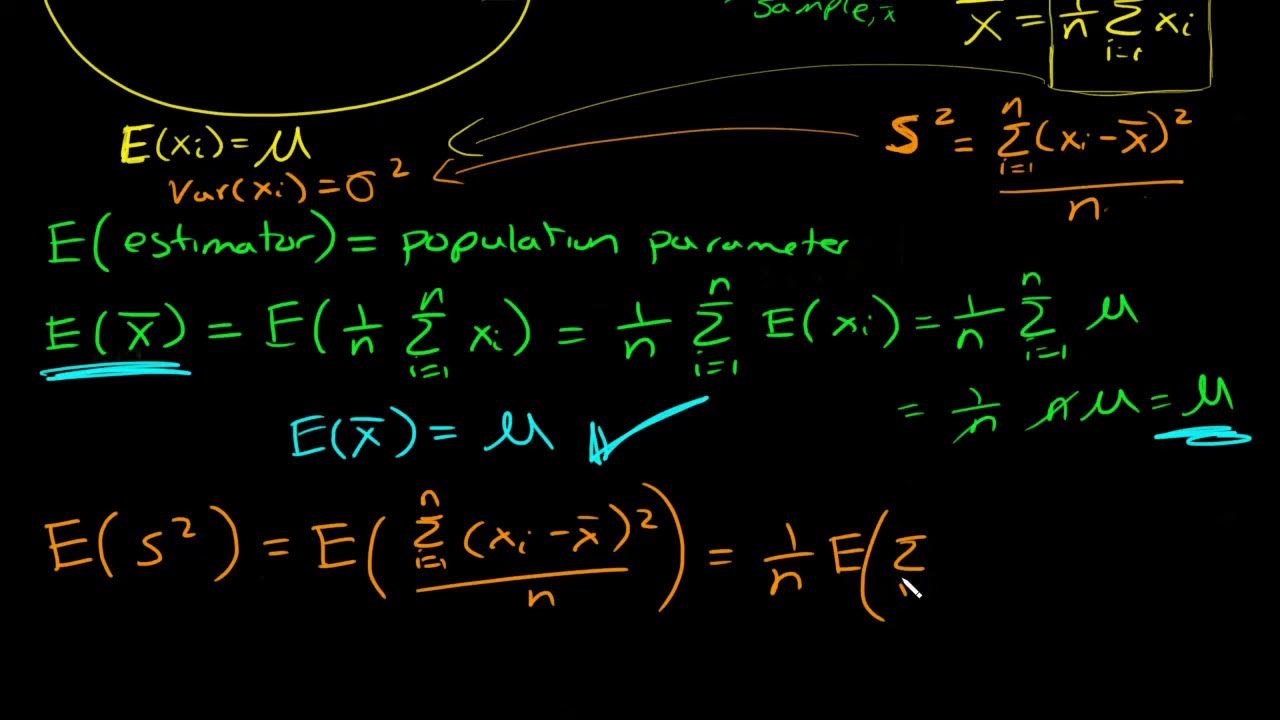
What is an unbiased estimator? Proof sample mean is unbiased and why we divide by n-1 for sample var
5.0 / 5 (0 votes)
Thanks for rating: