Can You Find Mean, Variance, & Standard Deviation of a Frequency Grouped DataTable? Simple Tutorial

PreMath
27 Oct 202010:05
EducationalLearning
32 Likes 10 Comments

TLDRThis tutorial demonstrates the calculation of mean, variance, and standard deviation from grouped data. It begins by explaining how to determine the mean, followed by a step-by-step process for calculating variance and standard deviation. The video uses a clear example with scores and their frequencies, guiding viewers through the process of finding midpoints, multiplying frequencies with their respective values, and finally computing the statistical measures. The result is a comprehensive understanding of these fundamental concepts in statistics.

Takeaways
  • πŸ“Š The tutorial focuses on calculating mean, variance, and standard deviation from grouped data consisting of scores and their frequencies.
  • πŸ“ˆ The mean (average) is calculated by multiplying each group's midpoint (x) by its frequency (f), summing these products, and then dividing by the total frequency.
  • πŸ”’ To find the midpoint of each group, add the lower and upper bounds of the score range and divide by two.
  • πŸ“Š Variance is calculated by taking the difference between each score (x) and the mean (xΜ„), squaring these differences, multiplying by the frequency (f), and summing the results.
  • πŸ“ˆ The variance for a sample is given by the sum of the squared differences divided by the total frequency minus one (n-1).
  • πŸ“Š The standard deviation is the square root of the variance and provides a measure of the dispersion or spread of the data around the mean.
  • πŸ”’ The process involves several steps: calculating the mean, finding the variance, and finally determining the standard deviation.
  • πŸ“‹ The script provides a clear and methodical approach to statistical analysis using grouped data.
  • πŸ“Š The use of sigma notation (Ξ£) is emphasized for summing values in the calculations.
  • πŸ”‘ Understanding these concepts is crucial for statistical analysis and interpretation of data sets.
  • πŸŽ“ The tutorial is educational and aimed at individuals looking to enhance their pre-mathematical or statistical skills.
  • πŸ“Ί The video content is engaging and informative, offering a step-by-step guide to complex calculations.
Q & A

  • What statistical concepts are covered in the video?

    -The video covers the calculation of mean, variance, and standard deviation from grouped data.

  • How is the midpoint of a grouped score determined?

    -The midpoint, represented by x, is determined by adding the lower and upper bounds of the group and dividing by 2.

  • What does the sigma notation (Ξ£) represent in statistics?

    -The sigma notation (Ξ£) represents the sum or addition of a series of values in statistics.

  • What is the formula used to calculate the mean from grouped data?

    -The mean, or x-bar, is calculated using the formula: mean = Ξ£ (frequency * x) / Ξ£ frequency.

  • How is the variance calculated for a sample in statistics?

    -The variance for a sample is calculated using the formula: variance = Ξ£ (frequency * (x - x-bar)^2) / (n - 1), where n is the number of observations.

  • What is the standard deviation and how is it related to variance?

    -The standard deviation is a measure of dispersion and is equal to the square root of the variance.

  • Why is it important to calculate standard deviation?

    -Calculating standard deviation is important as it provides insight into the variability or spread of data points around the mean, which is crucial for understanding data behavior and making statistical inferences.

  • What was the final calculated mean value in the video?

    -The final calculated mean value in the video was 27.

  • What was the final calculated variance value in the video?

    -The final calculated variance value in the video was 24.86.

  • What was the final calculated standard deviation value in the video?

    -The final calculated standard deviation value in the video was approximately 4.98.

  • How can the calculated statistical values help in understanding data?

    -The calculated statistical values, such as mean, variance, and standard deviation, provide a summarized understanding of data, allowing for the identification of central tendency, dispersion, and the degree of variation, which are essential for data analysis and interpretation.

Outlines
00:00
πŸ“š Introduction to Calculating Mean, Variance, and Standard Deviation

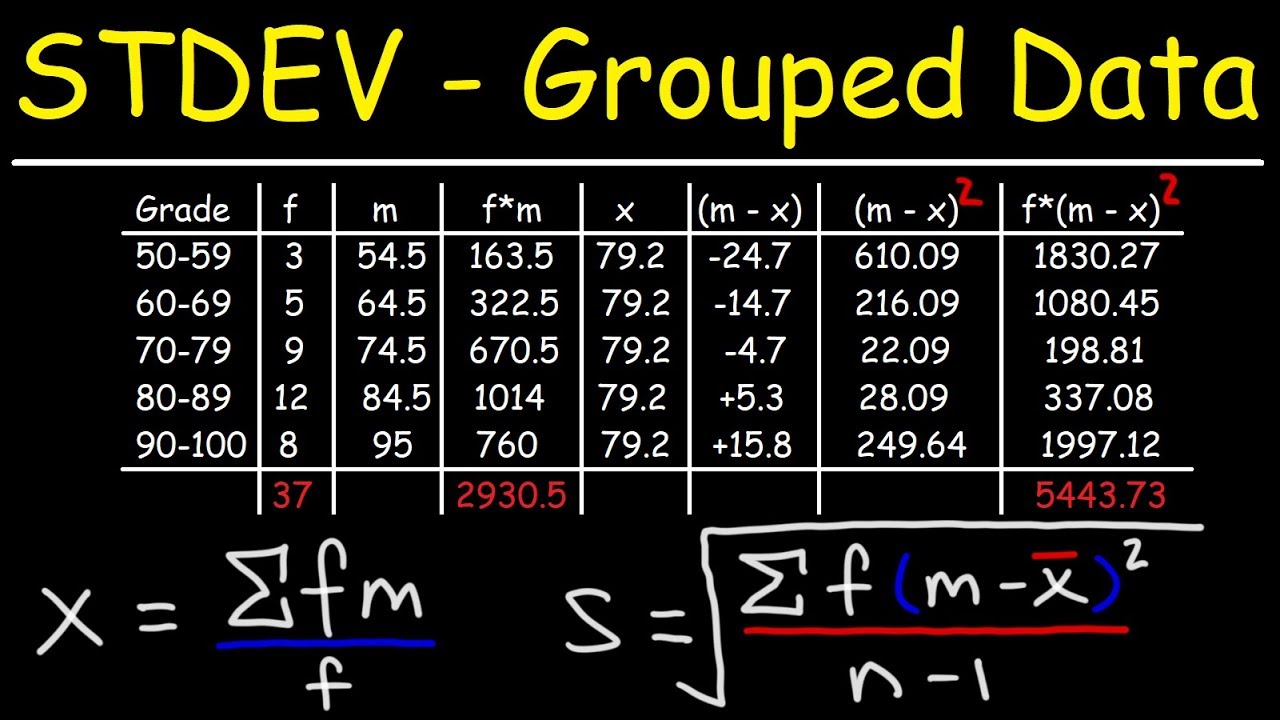
This paragraph introduces the topic of the video, which is to calculate the mean, variance, and standard deviation for a set of grouped data. The data is presented with scores in the first column and their frequencies in the second column. The process begins with calculating the mean by identifying the midpoint of each grouped score and using the corresponding frequencies to find the sum of the products of the midpoints and frequencies. The mean is then found by dividing this sum by the total frequency.

05:00
πŸ“ˆ Calculating Variance from Grouped Data

In this paragraph, the process of calculating variance from the grouped data is explained. It starts by finding the difference between each score (x) and the mean (x-bar) previously calculated. These differences are then squared, and for each score, the squared difference is multiplied by its frequency. The variance is then calculated by summing these products and dividing by the total frequency minus one, which accounts for the sample size. The paragraph also emphasizes that the formula used is for sample data.

10:03
πŸ“Š Determining the Standard Deviation

The final step in the video script is calculating the standard deviation. The standard deviation is the square root of the variance calculated in the previous paragraph. The paragraph provides the formula for standard deviation and applies it to the variance value obtained earlier. The result is the standard deviation, which gives an understanding of the spread or dispersion of the data set around the mean. The video concludes with a reminder to subscribe for more educational content.

Mindmap
Keywords
πŸ’‘mean
The mean, often referred to as the average, is a measure of central tendency that is calculated by summing up all the values in a data set and then dividing by the number of values. In the context of the video, the mean is determined by using the grouped scores and their corresponding frequencies to find a representative central value for the data set. The script demonstrates this by using the formula: mean = (sigma of f of x) / (sigma of f), where 'f of x' represents the frequency times the midpoint (x), and 'f' represents the total frequency.
πŸ’‘variance
Variance is a measure of the spread or dispersion of a set of values. It quantifies how much the individual data points deviate from the mean, providing insight into the variability or consistency within the data set. The calculation of variance involves finding the difference between each data point and the mean, squaring these differences, and then averaging them. In the video, variance is computed using the formula for a sample, which accounts for the finite number of observations by including a division by (sigma of f) - 1, where 'sigma of f' is the total frequency of the data points.
πŸ’‘standard deviation
The standard deviation is a widely used measure of dispersion that indicates the degree of variation or spread in a set of values. It is the square root of the variance and provides an understanding of the average distance between each data point and the mean. The standard deviation is particularly useful because it is in the same units as the data, making it easier to interpret. In the video, the standard deviation is calculated by taking the square root of the previously computed variance, which results in a value of 4.986, indicating the average deviation of the scores from the mean.
πŸ’‘grouped data
Grouped data refers to a data set that has been organized into intervals or groups based on similar values. This method of organization simplifies the analysis of data by allowing for the calculation of statistics such as the mean, variance, and standard deviation using the midpoints of the groups and the corresponding frequencies. In the video, the data is presented in a table with columns for scores, frequencies, and other derived values, facilitating the computation of key statistical measures.
πŸ’‘midpoint
The midpoint of a grouped data interval is the average value that lies at the center of the range of scores for that group. It is typically calculated by adding the lower and upper bounds of the interval and dividing by two. Midpoints are essential in the analysis of grouped data because they represent the central value around which the scores in each group are clustered. In the video, the midpoints are calculated for each group to facilitate the computation of the mean and other statistical measures.
πŸ’‘frequency
Frequency refers to the number of times a particular value or score occurs in a data set. It is a fundamental concept in statistics that helps describe the distribution of data. In the context of grouped data, the frequency indicates how many times each score or midpoint falls within the specified interval. Frequencies are crucial for calculating statistics such as the mean, as they weight the contribution of each group to the overall data set.
πŸ’‘sigma notation
Sigma notation, represented by the Greek letter 'Οƒ' (sigma), is a mathematical symbol used to denote the sum of a series of terms. In statistics, it is often used to represent the sum of a dataset or the sum of a particular function applied to the dataset, such as the sum of frequencies or the sum of the product of frequencies and scores. The video script utilizes sigma notation to express the summation process required for calculating the mean, variance, and standard deviation.
πŸ’‘score
A score in the context of the video refers to the individual values that make up the dataset. These scores are the raw data points that are organized into groups for the purpose of statistical analysis. Scores are the fundamental building blocks of any statistical computation and are used to calculate various descriptive statistics such as the mean, variance, and standard deviation.
πŸ’‘calculation
Calculation refers to the process of performing mathematical operations to derive results from given values or data. In the context of the video, calculations are performed to determine statistical measures such as the mean, variance, and standard deviation from a set of grouped data. These calculations are essential for understanding the central tendency and dispersion of the data.
πŸ’‘descriptive statistics
Descriptive statistics are numerical measures that describe the characteristics of a data set, such as its central tendency, dispersion, and shape. They provide a summary of the data and are used to make inferences about the population from which the data was drawn. In the video, the mean, variance, and standard deviation are examples of descriptive statistics that are computed to describe and summarize the features of the grouped data.
πŸ’‘data analysis
Data analysis is the process of examining and interpreting data to extract meaningful insights, draw conclusions, and make informed decisions. It involves the application of statistical methods and techniques to understand patterns, relationships, and trends within the data. In the video, data analysis is demonstrated through the step-by-step computation of statistical measures from grouped data, which helps in understanding the underlying patterns and characteristics of the scores.
Highlights

The tutorial begins with an introduction to calculating mean, variance, and standard deviation for grouped data.

The first step is to calculate the mean, which involves using grouped scores and their corresponding frequencies.

Midpoints of the grouped scores are found by averaging the upper and lower bounds of each group.

The mean is calculated by multiplying each score's midpoint by its frequency and then dividing by the total frequency.

The second step is to calculate the variance, which requires finding the difference between each score's midpoint and the mean.

The differences are then squared and multiplied by their respective frequencies.

Variance is determined by taking the sum of the squared differences multiplied by their frequencies and dividing by the number of observations minus one.

The standard deviation is the final calculation, which is the square root of the variance.

The tutorial provides a clear and methodical approach to statistical analysis using grouped data.

The process of calculating the mean is demonstrated with a step-by-step explanation and example.

The calculation of variance is detailed, emphasizing the importance of each step in the process.

The standard deviation calculation is presented as the final statistical measure derived from the data.

The tutorial's structured format allows for easy understanding and application of statistical concepts.

The use of sigma notation is explained in the context of summing values in statistical calculations.

The tutorial's practical application of statistical formulas helps in grasping the concepts more effectively.

The final results of the mean, variance, and standard deviation are clearly presented for easy reference.

The tutorial encourages viewers to subscribe for more educational content on statistical analysis.

Transcripts

Browse More Related Video

Find the Mean, Variance, & Standard Deviation of Frequency Grouped Data Table| Step-by-Step Tutorial

How To Calculate The Standard Deviation of Grouped Data

Mean deviation, variance and standard deviation of grouped data.

Measures of Dispersion (Grouped Data) | Basic Statistics

How to Find the Standard Deviation, Variance, and Mean of a Sample and a Population - Easy Tutorial

How to calculate Standard Deviation and Variance

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathematicsStatisticsTutorialMean CalculationVarianceStandard DeviationGrouped DataEducational ContentData AnalysisMath Tutorial