Symbols commonly used in statistics

Diane R Koenig
28 Sept 201106:51
EducationalLearning
32 Likes 10 Comments

TLDRThe video script introduces fundamental concepts in statistics, emphasizing the distinction between a population and a sample. It explains that a population encompasses all elements of interest, while a sample is a subset of the population. The script further clarifies that parameters, represented by Greek letters, are measurements calculated from the entire population, whereas statistics, denoted by English letters, are derived from samples. Specific notations for mean, standard deviation, variance, and proportion are detailed, highlighting the difference in symbols and calculations between population and sample statistics.

Takeaways
  • 📚 In statistics, it's crucial to differentiate between a 'population', which is the entire group of interest, and a 'sample', which is a subset of the population.
  • 🔢 The term 'parameter' refers to a measurement calculated from the entire population, and it remains constant over time.
  • 📈 'Statistic' is used to describe measurements calculated from a sample of the population, which may vary if different samples are taken.
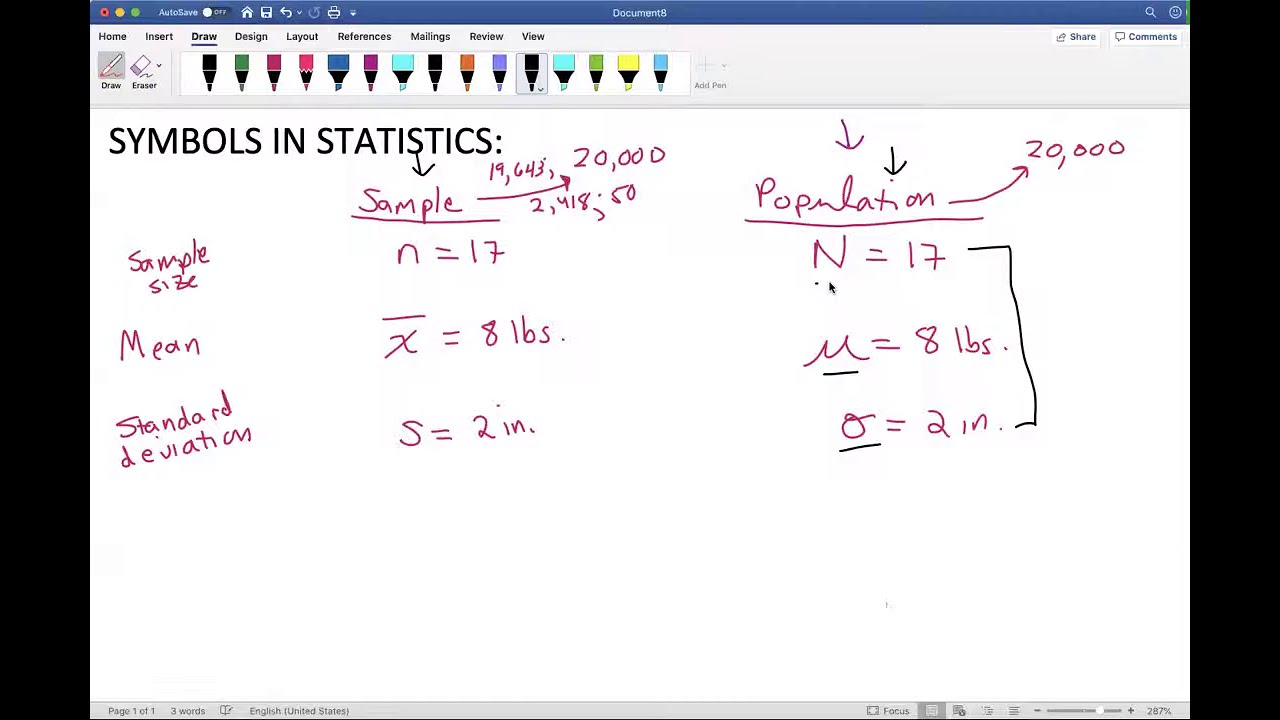
  • 🅰️ The notation for the population mean is the Greek letter mu (μ), while the sample mean is denoted by X with a bar over it (X̄).
  • 📊 The standard deviation for the population is represented by the Greek letter Sigma (σ), and for the sample, it's denoted by the letter 's'.
  • 📝 Variance is the square of the standard deviation, and its notation reflects this by squaring the symbol used for standard deviation.
  • 🎯 For proportions, the convention differs slightly. The population proportion is represented by 'P', and the sample proportion by 'p̂' (P with a hat over it).
  • 🔑 When using statistical tools like graphing calculators, it's important to distinguish between Greek and English alphabet notations as they indicate whether the calculation is for a population or a sample.
  • 🌟 Understanding these basic statistical terms and notations is essential for accurate data interpretation and communication.
  • 📊 Parameters and statistics are foundational to statistical analysis, and correctly identifying them is key to making valid conclusions from data.
  • 🔄 The process of drawing samples and calculating statistics from them allows for inferences about the larger population, which is a cornerstone of statistical analysis.
Q & A

  • What is the main difference between a population and a sample in statistics?

    -A population in statistics refers to the entire set of elements or individuals of interest for a particular study, while a sample is a subset of these elements drawn from the population.

  • What are parameters in the context of statistical formulas?

    -Parameters are measurements calculated from a population. They represent the true characteristics of the entire group being studied and do not change, such as the population mean or standard deviation.

  • How are statistics different from parameters?

    -Statistics are calculations derived from a sample of the population, unlike parameters which are derived from the entire population. Statistics provide estimates for the parameters and may vary with different samples.

  • What is the notation used for the population mean?

    -The population mean is denoted by the Greek letter mu (µ).

  • How is the sample mean represented in statistical notation?

    -The sample mean is represented by the letter 'X' with a bar over it (X̄), indicating that it is an estimated value from a subset of the population.

  • What is the standard deviation and how is it related to variance?

    -Standard deviation is a measure of the amount of variation or dispersion in a set of values. It is the square root of the variance, which is the average of the squared differences from the mean.

  • What notation is used for the population standard deviation?

    -The population standard deviation is symbolized by the Greek letter Sigma (Σ).

  • How is the sample standard deviation denoted in statistical notation?

    -The sample standard deviation is denoted by the letter 's' (lowercase), following the convention of using letters from the English alphabet for sample statistics.

  • What is variance and how is it notated in statistics?

    -Variance is the square of the standard deviation and represents the average of the squared differences from the mean. For the population variance, it is notated using the Greek letter Sigma (Σ) with a squared symbol (Σ²), and for the sample variance, it is denoted as 's²'.

  • Why is the convention for denoting population proportion different from other statistical notations?

    -The convention for denoting population proportion is different because the Greek letter pi (π) was initially used but led to confusion with its geometric meaning. Therefore, a small 'p' is used for population proportion, and 'p̂' (p with a hat) is used for sample proportion.

  • How can one distinguish between population and sample statistics on a graphing calculator?

    -On a graphing calculator, population statistics are typically denoted with Greek letters, while sample statistics are denoted with English alphabet letters. Users should look for the correct notation on the calculator's screen to find the appropriate calculation.

  • What is the significance of understanding statistical notations and parameters?

    -Understanding statistical notations and parameters is crucial for accurately interpreting and communicating statistical findings. It allows for clear distinction between estimated values from samples and true values from populations, ensuring the viability and reliability of statistical analysis.

Outlines
00:00
📚 Introduction to Statistical Terminology

This paragraph introduces essential statistical terms such as population and sample. A population refers to the entire set of elements under study, while a sample is a subset of the population. The paragraph emphasizes the importance of understanding these concepts and the distinction between them. Parameters are measurements calculated from the entire population and remain constant, represented by Greek letters. In contrast, statistics are derived from samples and are subject to variation, denoted by English alphabet letters. The paragraph also explains the notations for the mean (μ for population, x̄ for sample) and touches on the concepts of standard deviation and variance, with their respective symbols (σ for population, s for sample).

05:00
📈 Understanding Notations for Variance and Proportion

This paragraph delves deeper into the notations used for variance and proportion in statistical analysis. Variance is defined as the square of the standard deviation, with the population variance denoted by σ² and the sample variance by s². The paragraph clarifies the distinction in notation for population and sample statistics, highlighting the use of Greek letters for population parameters and English alphabet letters for sample statistics. The discussion then shifts to proportions, explaining the unconventional use of the letter 'p' for population proportion and 'p̂' for sample proportion. This deviation from the standard practice was necessary to avoid confusion with the mathematical constant pi (π). The paragraph concludes by reinforcing the importance of recognizing these symbols in a statistics course, providing a comprehensive overview of the key notations and their applications.

Mindmap
Keywords
💡Population
In statistics, a population refers to the entire set of individuals or elements that are of interest for a particular study. It represents the complete group from which data can be collected. For example, if we want to understand the average height of all students in a school, the entire student body is the population of interest.
💡Sample
A sample is a subset of the larger population from which data is collected for analysis. It is used when it is impractical or impossible to collect data from every single member of the population. In the context of the video, a sample is 'a whole of some of the elements out of that population of interest', and the data derived from it are called statistics.
💡Parameter
Parameters are numerical values that describe characteristics of a population. These include the population mean, standard deviation, and variance. Parameters are considered fixed and do not change because they are derived from the entire population. The video script explains that parameters are 'measurements...calculated from the population' and they 'don't change'.
💡Statistic
Statistics are numerical values that describe characteristics of a sample. They are estimates of the corresponding parameters of the population and are derived from a subset of the data. The video script clarifies that statistics are 'information...calculated from a sample of information', highlighting that they may vary with different samples.
💡Mean
The mean, or average, is a measure of central tendency that is calculated by adding up all the values in a dataset and dividing by the number of values. It provides an idea of the typical or central value in a set of data. In the video, the mean of the population is denoted by the Greek letter mu (μ), while the sample mean is denoted by X with a bar over it (X̅).
💡Standard Deviation
The standard deviation is a measure of the amount of variation or dispersion in a set of values. It indicates how much the individual data points in a dataset typically deviate from the mean. The standard deviation of a population is denoted by the Greek letter Sigma (σ), while the sample standard deviation is denoted by the letter 's'.
💡Variance
Variance is a measure of the spread of data points around the mean and is calculated as the square of the standard deviation. It quantifies the average of the squared differences from the mean. The notation for population variance is the square of the standard deviation symbol (σ²), and for sample variance, it is the 's' with a square (s²).
💡Proportion
A proportion is a fraction or a ratio that represents the part-to-whole relationship between two quantities. In statistics, it often refers to the percentage or fraction of a population that possesses a certain attribute. The video script notes that while the convention for parameters is to use Greek letters, for population proportion, the symbol 'P' is used instead of a Greek letter to avoid confusion with the mathematical constant pi (π).
💡Notation
Notation in statistics refers to the symbols and abbreviations used to represent specific statistical concepts and measurements. The video script emphasizes the importance of understanding notations such as Greek letters for population parameters and letters from the English alphabet for sample statistics, as they help in distinguishing between parameters and statistics.
💡Estimation
Estimation in statistics involves using sample data to make inferences about the characteristics of the population from which the sample was drawn. It is a process of approximation, where statistics derived from a sample are used to estimate parameters of the population.
💡Data Analysis
Data analysis is the process of examining, cleaning, transforming, and modeling data to extract useful information, draw conclusions, and support decision-making. It involves the use of statistical methods and tools to analyze data and derive insights from it.
Highlights

The importance of understanding statistical formulas and their terminologies.

The distinction between a population and a sample in statistical analysis.

A population represents the entire group of interest for a study.

A sample is a subset of elements from the population of interest.

Parameters are measurements calculated from the entire population.

Statistics are derived from a sample of a population.

Greek letters are typically used to denote population parameters.

English alphabet letters are used for sample statistics.

The symbol for population mean is the Greek letter mu (μ).

The sample mean is denoted as X̅ (X-bar).

The formula for mean calculation remains the same, whether for population or sample.

The population standard deviation is represented by the Greek letter Sigma (σ).

The sample standard deviation is denoted as s or S̅.

Variance is the square of the standard deviation.

Population variance is symbolized as σ², and sample variance as s².

For population proportion, the symbol is P, and for sample proportion, it's ŷ (P-hat).

The use of different notations for proportion parameters to avoid confusion with geometry terms.

Transcripts

Browse More Related Video

Statistics: Populations & Samples and Parameters vs Statistics

Populations, Samples, Parameters, and Statistics

Symbols in statistics. Sample or Population?

Parameter vs Statistic

Statistics - The vocabulary of statistics

Introduction to sampling distributions | Sampling distributions | AP Statistics | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Statistics BasicsPopulation vs SampleParameters vs StatisticsMean CalculationStandard DeviationVariance ExplanationGreek and English NotationStatistical SymbolsData AnalysisEducational Content