Intermediate value theorem | Existence theorems | AP Calculus AB | Khan Academy

Khan Academy

15 Jul 201608:04

EducationalLearning

32 Likes 10 Comments

TLDRThe video script introduces the Intermediate Value Theorem, emphasizing its intuitive nature within mathematics. It explains that for a continuous function F over a closed interval [A, B], the function will take on every possible value between F(A) and F(B). The theorem is illustrated with examples and the concept of continuity is clarified by explaining that the function's graph can be drawn without lifting the pencil. The video aims to provide an intuitive understanding of the theorem without a formal proof, highlighting its fundamental role in mathematical analysis.

Takeaways

📚 The Intermediate Value Theorem is a fundamental concept in mathematics, known for its intuitive nature.
📈 The theorem applies to continuous functions defined over a closed interval, including the endpoints A and B.
🔍 A continuous function is one where the limit at any point is equal to the function's value at that point, ensuring the function is well-defined and unbroken.
🌐 The theorem can be visualized by drawing the function's graph over the interval without lifting the pen, signifying the function's continuity.
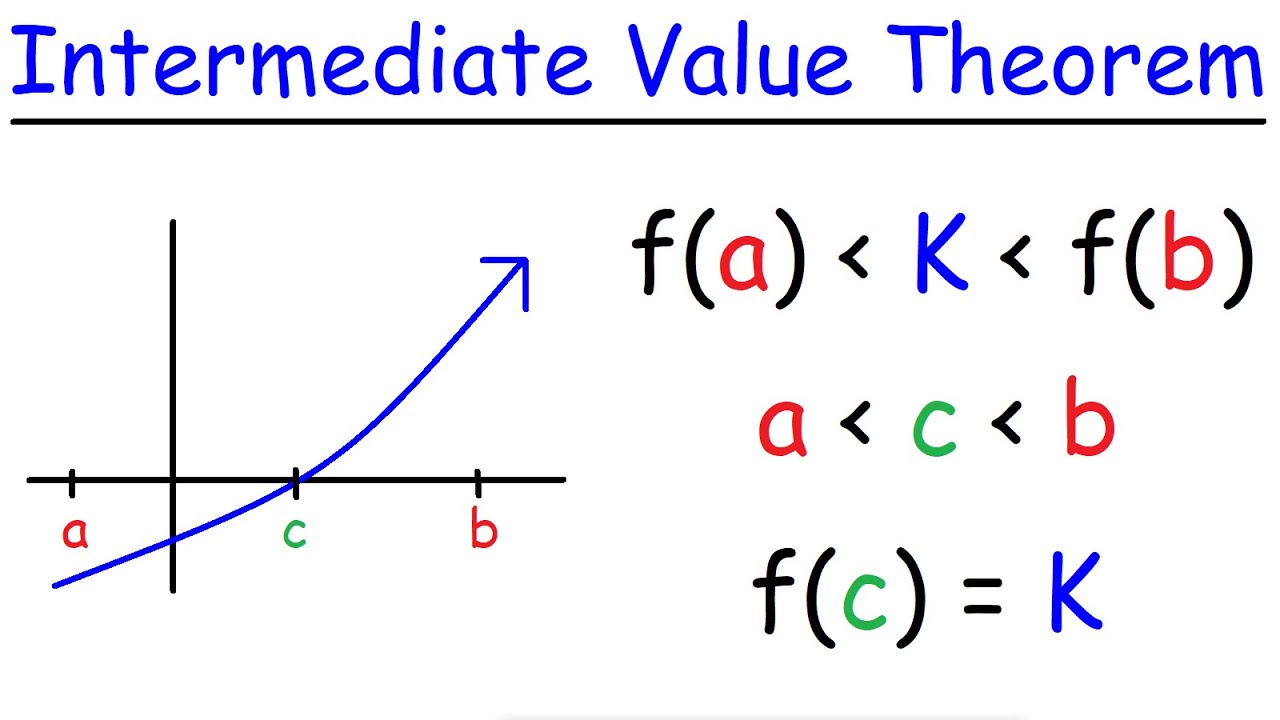
📊 The Intermediate Value Theorem asserts that a continuous function will take on every value between F(A) and F(B) at least once within the interval.
🔎 For any value L between F(A) and F(B), there exists at least one number C in the interval [A, B] such that F(C) equals L.
🤔 Attempting to draw a function where the theorem does not hold (i.e., missing a value L) is practically impossible for a truly continuous function.
🏦 The theorem's validity is inherent to the nature of continuous functions; any gap in values would disrupt the continuity, which contradicts the function's definition.
📝 The script does not provide a formal proof of the theorem but encourages an intuitive understanding of its principles.
🎓 Understanding the Intermediate Value Theorem is crucial for anyone studying mathematics as it has wide-ranging applications and implications.
🌟 The theorem highlights the power and beauty of mathematical concepts, which, despite their abstract nature, often reflect common sense and logical consistency.

Q & A

What is the main topic of the video?
-The main topic of the video is the Intermediate Value Theorem, a fundamental concept in mathematics.
How is the Intermediate Value Theorem described in the video?
-The Intermediate Value Theorem is described as one of the more intuitive theorems in mathematics, possibly the most intuitive theorem one might encounter.
What is the precondition for the Intermediate Value Theorem to apply?
-The precondition for the Intermediate Value Theorem to apply is that the function F must be continuous at every point of the closed interval [A, B].
What does it mean for a function to be continuous at every point?
-For a function to be continuous at every point, it must be defined at every point, and the limit of the function at that point must be equal to the value of the function at that point.
How can you visualize a continuous function over an interval?
-You can visualize a continuous function over an interval by imagining that you can draw the graph of the function between any two points without lifting your pencil off the paper.
What does the first statement of the theorem imply about the function F?
-The first statement of the theorem implies that the function F will take on every value between F(A) and F(B) over the interval [A, B].
How does the second statement of the theorem describe the theorem?
-The second statement of the theorem describes that for any value L between F(A) and F(B), there exists a number C in the closed interval [A, B] such that F(C) equals L.
What is the significance of the Intermediate Value Theorem?
-The significance of the Intermediate Value Theorem is that it provides a fundamental understanding of the behavior of continuous functions, ensuring that they take on all values between their endpoints within a given interval.
How does the video attempt to build an intuition for the theorem?
-The video attempts to build an intuition for the theorem by using visual examples and explaining the concept of continuity, as well as by challenging the viewer to try to draw a function that would contradict the theorem.
What is the conclusion drawn from the video about the Intermediate Value Theorem?
-The conclusion drawn from the video is that the Intermediate Value Theorem is a common-sense theorem for continuous functions, which ensures that they must take on every value between their endpoints when graphed over a closed interval.

Outlines

00:00

📚 Introduction to the Intermediate Value Theorem

This paragraph introduces the concept of the Intermediate Value Theorem, emphasizing its intuitive nature despite the mathematical terminology often associated with it. The voiceover explains that the theorem will be read out and interpreted, but not proven, in this session. The theorem states that for a continuous function F over a closed interval including points A and B, it must be defined at every point within that interval. The explanation includes a visual representation of what a continuous function might look like over the interval, highlighting that it must be defined and continuous at every point. The paragraph also describes how to visualize a continuous function by imagining it as drawing the function's graph without lifting the pencil, thus ensuring continuity.

05:00

🔢 Explanation of the Intermediate Value Theorem's Conclusions

This paragraph delves into the two ways the conclusion of the Intermediate Value Theorem can be stated. The first statement suggests that a continuous function will take on every value between F of A and F of B over the interval. The second statement asserts that for any value L between F of A and F of B, there exists at least one number C within the interval such that F of C equals L. The paragraph further illustrates this by considering hypothetical scenarios where multiple values of C could correspond to a single L, indicating the theorem's applicability in various cases. It also presents a thought experiment, challenging the viewer to draw a function where the first statement is true but the second is not, ultimately demonstrating the inherent logic and necessity of the theorem's conclusions within the context of continuous functions.

Mindmap

Keywords

💡Intermediate Value Theorem

The Intermediate Value Theorem is a fundamental concept in calculus that states if a function is continuous on a closed interval [A, B], then it will take on any value between F(A) and F(B). This theorem is intuitive and demonstrates the completeness property of continuous functions. In the video, the theorem is explained with the idea that you can draw the function's graph over the interval without lifting your pencil, indicating the function's continuity, and it will cover every value between the function's values at the endpoints A and B.

💡Continuous Function

A continuous function is one that is defined at every point in its domain and where the function's value changes smoothly without any jumps or breaks in the graph. In the context of the video, the continuity of a function is crucial for the Intermediate Value Theorem to hold true. The video explains that if a function is continuous over an interval, you can draw its graph without lifting your pencil, which means there are no gaps or jumps in the function's values.

💡Closed Interval

A closed interval in mathematics is an interval that includes its endpoints. In the context of the video, when discussing the Intermediate Value Theorem, the function is continuous on a closed interval [A, B], which means it includes the endpoints A and B and is continuous between them. This is important for the theorem because it ensures that the function's behavior is consistent across the entire range of values from A to B, including the endpoints.

💡Function Values

Function values refer to the outputs or results produced by a function for a given input. In the video, the function values at the endpoints A and B are denoted as F(A) and F(B), respectively. These values are important because they define the range of possible values the function can take on within the interval. The Intermediate Value Theorem asserts that for a continuous function on a closed interval, all values between F(A) and F(B) will be assumed by the function at some point.

💡Graph

In mathematics, a graph is a visual representation of the function's behavior, plotting the function's values against its inputs. The video uses the concept of a graph to illustrate how a continuous function can be drawn without lifting the pencil, which indicates the function's continuity and its coverage of all values between F(A) and F(B). The graph is a key tool in visualizing and understanding the Intermediate Value Theorem.

💡Endpoints

Endpoints refer to the first and last points of an interval. In the context of the video, A and B are the endpoints of the closed interval [A, B]. The function's continuity at these points, along with the rest of the interval, is what allows the Intermediate Value Theorem to be applicable. The theorem's conclusion involves the function values at these endpoints and the values between them.

💡Limits

In calculus, limits are used to describe the behavior of a function as the input approaches a certain value. For a function to be continuous at a point, the limit of the function as the input approaches that point must be equal to the function's value at that point. The video implies the concept of limits when discussing the continuity of a function, which is necessary for the Intermediate Value Theorem to apply.

💡Intuition

Intuition refers to the ability to understand or sense something without the need for conscious reasoning. In the context of the video, the presenter aims to develop an intuitive understanding of the Intermediate Value Theorem. By using visual examples and metaphors, such as drawing the function's graph without lifting the pencil, the video helps viewers grasp the theorem's concept without delving into formal proofs.

💡Mathematical Career

A mathematical career typically refers to professional paths that involve the study, application, or teaching of mathematics. In the video, the Intermediate Value Theorem is described as a concept that is likely to be encountered multiple times throughout one's mathematical career, indicating its fundamental and recurring importance in the field of mathematics.

💡Conceptual Underpinning

Conceptual underpinning refers to the fundamental ideas or principles that form the basis of a theory or concept. In the video, the presenter emphasizes the conceptual underpinning of the Intermediate Value Theorem, aiming to help viewers understand the core idea behind the theorem without getting into the technical details or proofs.

Highlights

The Intermediate Value Theorem is one of the most intuitive theorems in mathematics.

The theorem applies to functions that are continuous at every point of a closed interval, including the endpoints A and B.

A continuous function is defined at every point and its limit at a point equals the function's value at that point.

The function must be defined at the endpoints F of A and F of B.

Continuous functions can be visualized as graphs that can be drawn without lifting the pen from the paper.

The Intermediate Value Theorem states that a continuous function will take on every value between F of A and F of B over the interval.

For any value L between F of A and F of B, there exists a number C in the interval such that F of C equals L.

The theorem can be restated as the function taking on every possible value in the range between the function's values at the interval endpoints.

The theorem's intuitive nature becomes clear when trying to draw a function that does not satisfy its conditions.

Attempting to draw a function that skips a value L between F of A and F of B inevitably results in lifting the pen.

The Intermediate Value Theorem is a fundamental concept that provides a good intuition for understanding continuous functions.

The theorem is applicable to a wide range of mathematical problems and has practical applications in various fields.

The theorem's proof is not provided in the video, but the conceptual understanding is emphasized through visual examples.

The video provides a clear and straightforward explanation of the theorem, making it accessible to a broad audience.

The theorem's implications are significant for the study of functions and their properties.

Understanding the Intermediate Value Theorem enhances problem-solving skills in mathematics.

The video's approach to explaining the theorem through visualization aids in comprehension and retention.

The theorem is a key component in the study of calculus and analysis.

Transcripts

Browse More Related Video

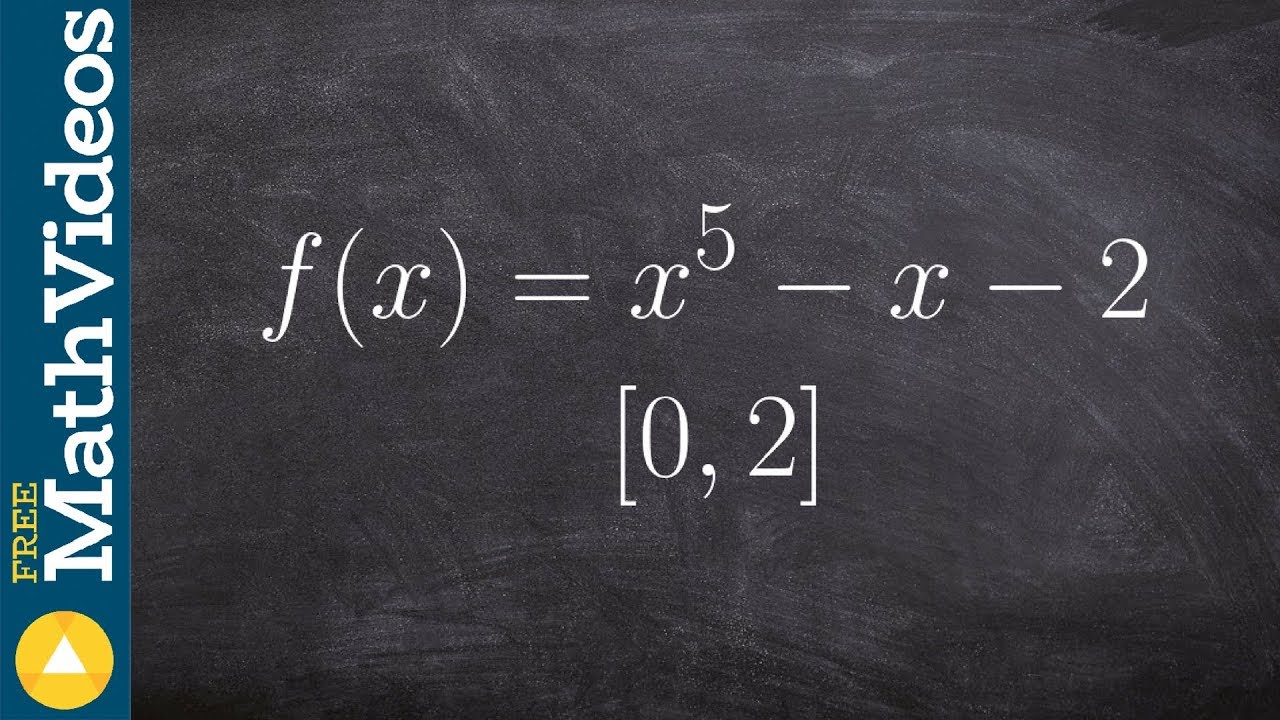
How to show that a solution exists to a functions using IVT

Intermediate value theorem example | Existence theorems | AP Calculus AB | Khan Academy

Using the Intermediate Value Theorem Examples

Intermediate Value Theorem

Calculus 1 Lecture 1.4: Continuity of Functions

AP Calculus AB - 1.16 Working with the Intermediate Value Theorem

Intermediate value theorem | Existence theorems | AP Calculus AB | Khan Academy

Takeaways

Q & A

What is the main topic of the video?

How is the Intermediate Value Theorem described in the video?

What is the precondition for the Intermediate Value Theorem to apply?

What does it mean for a function to be continuous at every point?

How can you visualize a continuous function over an interval?

What does the first statement of the theorem imply about the function F?

How does the second statement of the theorem describe the theorem?

What is the significance of the Intermediate Value Theorem?

How does the video attempt to build an intuition for the theorem?

What is the conclusion drawn from the video about the Intermediate Value Theorem?