AP Calculus AB - 1.16 Working with the Intermediate Value Theorem
TLDRIn this AP Calculus AB video, Mr. Bortnick discusses the Intermediate Value Theorem (IVT), a foundational concept for continuous functions. The IVT states that for a function to be continuous from 'a' to 'b', it must take on every value between the outputs of 'f(a)' and 'f(b)' at least once. Bortnick illustrates this with a graphical example and applies the theorem to a table of values to demonstrate how it ensures the existence of zeros and specific outputs within intervals. The lesson concludes with practice problems to solidify understanding of this key theorem in calculus.
Takeaways
- 📚 The Intermediate Value Theorem (IVT) is a fundamental concept in AP Calculus AB, introduced in Unit 1 on limits and continuity.
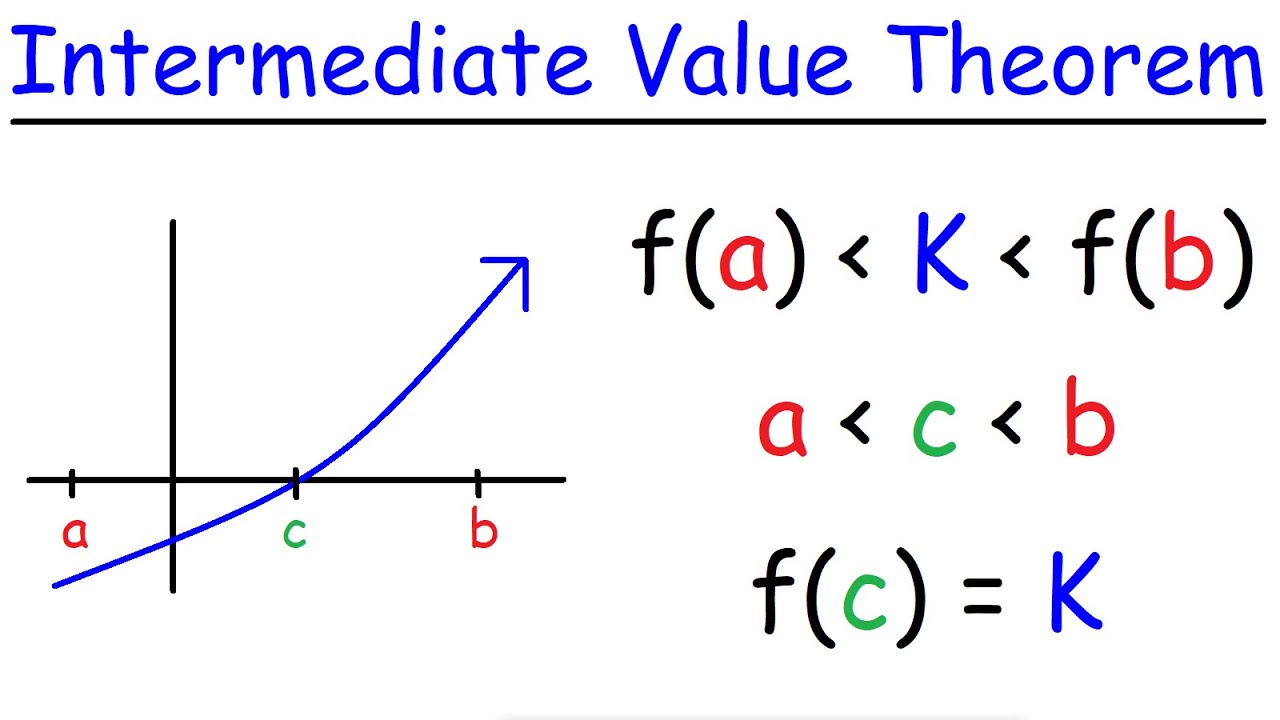
- 🔍 The IVT specifically applies to continuous functions and states that if a function is continuous from x=a to x=b, every value between the outputs f(a) and f(b) must exist at some point in the interval [a, b].
- 📈 Graphically, the IVT implies that a continuous function must cross any arbitrary y-value between f(a) and f(b) at least once within the interval [a, b].
- 📉 The IVT is crucial for understanding that a continuous function cannot 'jump' over a value between its endpoints without passing through that value.
- 📝 The video script uses a table of values to demonstrate the application of the IVT, emphasizing that the theorem only applies when the function is explicitly stated to be continuous.
- 🔑 The script provides an example of how to determine the minimum number of zeros a continuous function must have within a given interval, based on the values in the table.
- 🤔 The IVT does not guarantee the exact number of times a function will equal a specific value, only that there must be at least one occurrence within the interval if the value lies between the function's outputs at the endpoints.
- 📋 The script includes practice problems to help students apply the IVT, such as determining the minimum number of times a function equals zero or a specific value within a given interval.
- 📊 The IVT is foundational for many rules in AP Calculus and is essential for understanding the behavior of continuous functions.
- 💡 The video script concludes with an invitation for students to bring questions to class or office hours, highlighting the importance of engaging with the material and seeking clarification when needed.
- 🎓 The completion of this section marks the end of Chapter 1, with a review and a test to follow, indicating the progression of the course and the importance of mastering the IVT for further studies in calculus.
Q & A
What is the main topic of Unit 1.16 in AP Calculus AB?
-The main topic of Unit 1.16 in AP Calculus AB is the Intermediate Value Theorem (IVT).
Why is the Intermediate Value Theorem important?
-The Intermediate Value Theorem is important because it is a foundational rule in AP Calculus that ensures that for a continuous function, every value between the outputs at two endpoints exists at some point within the interval.
What does the Intermediate Value Theorem state?
-The Intermediate Value Theorem states that if a function f is continuous from x = a to x = b, then every value between the outputs f(a) and f(b) exists at some point in the interval [a, b].
What is a key requirement for the Intermediate Value Theorem to apply?
-A key requirement for the Intermediate Value Theorem to apply is that the function f must be continuous on the interval [a, b].
How does the Intermediate Value Theorem work graphically?
-Graphically, the Intermediate Value Theorem indicates that if you have a continuous function from x = a to x = b, you cannot move from the point (a, f(a)) to (b, f(b)) without crossing every value between f(a) and f(b) at least once.
What is an example of applying the Intermediate Value Theorem to find zeros of a function?
-If you have a function that changes from a positive value to a negative value over an interval, the Intermediate Value Theorem guarantees that there is at least one zero (where f(x) = 0) within that interval.
Why is it important to know that a function is continuous when using the Intermediate Value Theorem?
-It is important to know that a function is continuous because the Intermediate Value Theorem only applies to continuous functions. If the function has discontinuities, the theorem cannot be used.
How does the Intermediate Value Theorem help in solving problems on the AP exam?
-The Intermediate Value Theorem helps in solving problems on the AP exam by providing a method to prove the existence of certain values within an interval, such as zeros or specific function outputs, based on the continuity of the function.
What does the teacher emphasize about using the Intermediate Value Theorem in practice problems?
-The teacher emphasizes that the Intermediate Value Theorem can be used only if the function is continuous, and students should pay attention to whether continuity is specified in the problem.
What are students encouraged to do after learning about the Intermediate Value Theorem?
-Students are encouraged to try out the practice problems, check the test prep problems at the end of the chapter, and bring any questions they have to class or office hours.
Outlines
📚 Introduction to the Intermediate Value Theorem
In this introductory segment, Mr. Bortnick presents the topic of the Intermediate Value Theorem (IVT) in the context of AP Calculus AB. He explains that the IVT is the first of three major theorems that will be covered and is specifically applicable to continuous functions. The theorem states that if a function 'f' is continuous on an interval from 'a' to 'b', then every value between the outputs of 'f(a)' and 'f(b)' is achieved by the function at some point within that interval, including the endpoints. Mr. Bortnick illustrates this concept graphically by drawing a curve and explaining that for any value 'c' between 'f(a)' and 'f(b)', the function must cross the line 'y = c' at least once if it is continuous. This theorem is foundational in calculus and sets the stage for further exploration in the course.
🔍 Applying the Intermediate Value Theorem to Practice Problems
This paragraph delves into the practical application of the IVT through a series of problems based on a table of values for a continuous function 'f(x)'. Mr. Bortnick demonstrates how to use the IVT to determine the minimum number of zeros a function can have within a given interval, highlighting that the theorem guarantees the existence of at least one zero between any two points where the function's output changes sign. He further explains how to identify the fewest possible times the function equals a specific value within an interval, emphasizing that the IVT only ensures the existence of such points if they lie between the given outputs. The discussion includes the importance of knowing the function's continuity before applying the IVT and the limitations of the theorem when the function's behavior between certain points is unknown.
🤔 Exploring the Limits of the Intermediate Value Theorem
In the final paragraph, Mr. Bortnick addresses the limitations and possibilities of the IVT. He uses a table of values to explore whether there must be a value of 'x' for which 'f(x)' equals a specific number within a given interval. He clarifies that while the IVT does not guarantee the existence of such a point unless it is between two known outputs, it does not rule out the possibility. The explanation includes a clear distinction between what the IVT can confirm and what it cannot, reinforcing the understanding that the theorem is a powerful tool within its defined scope but does not provide absolute certainty beyond that. Mr. Bortnick concludes the section by encouraging students to practice applying the IVT to various problems and to bring any questions they have to class or office hours.
Mindmap
Keywords
💡Intermediate Value Theorem (IVT)
💡Continuous Function
💡Discontinuities
💡Graph
💡Interval Notation
💡Table of Values
💡Minimum Number of Zeros
💡Endpoints
💡Practice Problems
💡Test Prep
Highlights
Introduction to the Intermediate Value Theorem (IVT) as the last section of Chapter 1 in the AP Calculus AB course.
Explanation of the IVT for continuous functions, stating that every value between the outputs of 'f(a)' and 'f(b)' exists at some point in the interval [a, b].
Graphical representation of the IVT, illustrating how a continuous function must cross an arbitrary y-value between 'f(a)' and 'f(b)'.
Emphasis on the importance of the IVT as a foundational rule in AP Calculus, applicable only to continuous functions.
Demonstration of how to apply the IVT to a table of values for a continuous function to determine the minimum number of zeros.
Analysis of a specific table of values, showing the minimum of three zeros between the interval [0, 9] using the IVT.
Instruction on using the IVT to determine the fewest possible times 'f(x)' equals one on the interval [4, 9].
Clarification that the IVT guarantees 'f(x)' will hit the value one at least once between the interval [7, -1].
Application of the IVT to confirm the existence of an 'x' such that 'x * f(x)' equals two on the interval [0, 4].
Discussion on the possibility of 'f(x)' being equal to negative two on the interval [4, 8], noting it is possible but not guaranteed by the IVT.
Explanation of the difference between a guaranteed result by the IVT and a mere possibility within a continuous function's range.
Encouragement for students to practice applying the IVT with provided problems to solidify their understanding.
Mention of the upcoming review session and chapter test, indicating the importance of the IVT in the AP Calculus curriculum.
Invitation for students to bring questions to class or office hours for further clarification on the IVT and related topics.
Conclusion of the lesson with a reminder of the significance of the IVT in understanding continuous functions in calculus.
Transcripts
Browse More Related Video
Intermediate Value Theorem

Calculus AB/BC – 1.16 Intermediate Value Theorem

Using the Intermediate Value Theorem Examples

AP Calculus Review Three Theorems You Must Know (EVT, IVT, MVT)
How to show that a solution exists to a functions using IVT

Intermediate value theorem example | Existence theorems | AP Calculus AB | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: