Defining a function at a point to make it continuous | Limits | Differential Calculus | Khan Academy

Khan Academy
18 Sept 201304:56
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses the continuity of a function f(x) = (6x^2 + 18x + 12) / (x^2 - 4), which is undefined at x = ±2 due to division by zero. To address this, the script suggests simplifying the function and redefining f(-2) to be 3/2 to maintain continuity. The simplification process involves factoring and canceling out terms, resulting in a new expression that is equivalent to the original function for all x except x = ±2. The redefined function provides a continuous value at x = -2, resolving the discontinuity issue.

Takeaways
  • 📚 The original function, f(x) = (6x^2 + 18x + 12) / (x^2 - 4), is undefined at x = ±2 due to division by zero.
  • 🔍 To address continuity, we examine why the function is undefined and find that x^2 - 4 becomes zero when x is ±2, leading to an undefined denominator.
  • 🤔 The question posed is what value to assign to f(-2) to make the function continuous at that point, which requires simplifying the function.
  • 🌟 By factoring out a 6 from the numerator and recognizing the difference of squares in the denominator, the function can be simplified.
  • 🎓 The simplified expression is 6(x + 2)(x + 1) / (x + 2)(x - 2), which allows us to cancel out (x + 2) from the numerator and denominator, assuming x ≠ ±2.
  • 📈 The simplified function becomes 6(x + 1) / (x - 2) for x ≠ ±2, which is equivalent to the original function except at the undefined points.
  • 🔧 To make the function continuous at x = -2, we consider the value the simplified expression would take when x = -2, which is 3/2.
  • 🌈 By redefining f(x) for x = -2, we can maintain the equivalence of the function while ensuring continuity at the problematic point.
  • 👉 The new definition of f(x) is f(x) = (6x^2 + 18x + 12) / (x^2 - 4) for x ≠ ±2, and f(-2) = 3/2, allowing for a continuous function.
  • 📊 The continuity adjustment does not affect the function's value elsewhere, ensuring that the function's behavior remains consistent except at x = ±2.
  • 🎯 The key to solving this problem is understanding the nature of undefined points in a function and how to adjust the function to maintain its continuity.
Q & A

  • What is the original function given in the transcript?

    -The original function is f(x) = (6x^2 + 18x + 12) / (x^2 - 4).

  • Why is the function not defined at x equals positive or negative 2?

    -The function is not defined at x equals positive or negative 2 because in the denominator, x^2 - 4 becomes 0, leading to division by zero, which is undefined.

  • How can the original function be simplified?

    -The original function can be simplified by factoring out a 6 from the numerator and recognizing the denominator as a difference of squares, resulting in f(x) = 6(x + 2) / (x - 2)(x + 2).

  • What is the constraint on x when simplifying the function?

    -The constraint on x when simplifying the function is that x cannot be equal to negative 2 or positive 2, as this would lead to division by zero in the simplified expression.

  • What value should be assigned to f(-2) to make the function continuous at that point?

    -To make the function continuous at x = -2, f(-2) should be assigned the value of 3/2, which is the result of the simplified expression when x approaches -2.

  • How does the new definition of the function ensure continuity at x equals negative 2?

    -The new definition of the function ensures continuity at x equals negative 2 by explicitly stating that f(x) is equal to 3/2 when x is negative 2, matching the value that would have been obtained from the simplified expression.

  • What is the significance of rationalizing the denominator?

    -Rationalizing the denominator is important to avoid undefined expressions, such as division by zero, and to ensure that the function is continuous and well-defined for all values in its domain.

  • What are the two values for which the original function is not defined?

    -The original function is not defined for x equal to positive 2 and x equal to negative 2, as in both cases the denominator becomes zero.

  • How does the simplified expression help in understanding the behavior of the function?

    -The simplified expression helps in understanding the behavior of the function by making it clear where the function is not defined and by providing a form that is easier to analyze and work with.

  • What is the role of factoring in the simplification process?

    -Factoring plays a crucial role in the simplification process by allowing us to break down complex expressions into simpler components, which can then be manipulated or canceled out to achieve a more straightforward form.

  • How does the concept of continuity affect the domain of a function?

    -The concept of continuity affects the domain of a function by limiting it to the values for which the function is well-defined and does not have any undefined points or gaps.

Outlines
00:00
📚 Understanding Function Continuity and Undefined Points

This paragraph discusses the continuity of a function, f(x) = (6x^2 + 18x + 12) / (x^2 - 4), and identifies that it is not defined at x = ±2 due to division by zero. The speaker simplifies the function to understand its behavior and explores the possibility of redefining f(x) at x = -2 to achieve continuity. By factoring and simplifying the expression, it is determined that f(x) can be equivalently represented as (6x + 1) / (x - 2) for x ≠ ±2. The paragraph concludes that to make f(x) continuous at x = -2, f(-2) should be redefined to 3/2.

Mindmap
Keywords
💡function
In mathematics, a function is a relation that assigns a single output value to each input value. In the context of the video, the function f(x) is given by an equation and the goal is to make this function continuous at a specific point, x = -2. The function is initially undefined at x = ±2 due to division by zero.
💡continuous
A continuous function is one where there are no breaks, gaps, or jumps in the graph of the function. In the video, the objective is to find a value for f(-2) that ensures the function is continuous even where it was previously undefined, thus maintaining a smooth curve across all x-values.
💡undefined
In mathematics, a function is said to be undefined at a point when it does not have a value or is not defined for a particular input. In the video, the function f(x) is undefined at x = ±2 because the denominator becomes zero, which is the result of division by zero, an operation that is not mathematically defined.
💡factoring
Factoring is the process of breaking down a polynomial into a product of other polynomials or factors. In the video, factoring is used as a method to simplify the function f(x) and to find a form that is continuous at x = -2.
💡simplify
To simplify in mathematics means to make an equation or expression easier to understand or work with. In the video, the function f(x) is simplified to find a form that is continuous at x = -2, which involves dividing both the numerator and the denominator by a common factor.
💡denominator
The denominator of a fraction is the part below the line from which the value of the fraction is calculated. In the video, the denominator of the original function becomes zero when x = ±2, which leads to the function being undefined at those points.
💡division by zero
Division by zero is an undefined operation in mathematics because zero cannot be a divisor as it does not represent a quantity that can be evenly distributed. In the video, the issue of division by zero arises when the denominator becomes zero, which is not allowed.
💡equivalence
In mathematics, two expressions are equivalent if they have the same value for all values of the variable in their domain. The video aims to find a value for f(-2) that makes the modified function equivalent to the original one at all points except x = -2.
💡constraint
A constraint is a limitation or restriction placed on a variable or a set of variables. In the video, the constraint is that x cannot be equal to ±2 because it would lead to division by zero, which is undefined.
💡re-engineer
Re-engineering is the process of rethinking and redesigning a system or function to improve its performance or to make it suitable for new requirements. In the video, re-engineering the function involves changing its definition at x = -2 to ensure continuity.
💡value assignment
Value assignment is the process of defining or assigning a specific value to a variable or function at a particular point. In the video, value assignment is used to determine what value should be given to f(-2) to make the function continuous at that point.
Highlights

The function f(x) is defined as 6x^2 + 18x + 12 over x^2 - 4, but it is not defined at x = ±2.

At x = ±2, the denominator becomes zero, leading to division by zero, which is undefined.

The goal is to find a value for f(-2) that makes the function continuous at that point.

The original function f(x) can be simplified by factoring out a 6 from each term in the numerator.

The denominator is a difference of squares, which can be factored into (x + 2)(x - 2).

By factoring, the expression simplifies to 6(x + 2) over (x + 2)(x - 2), with the constraint that x ≠ ±2.

The simplified expression is 6(x + 1) over (x - 2) for x ≠ ±2.

To ensure continuity at x = -2, the function needs to be redefined so that f(-2) equals the value of the simplified expression when x = -2.

When x = -2, the simplified expression evaluates to 3/2.

By setting f(-2) to 3/2, the function becomes continuous at x = -2.

The redefined function f(x) is equivalent to the original function except at x = ±2.

The process of simplifying and redefining the function at a specific point demonstrates a method for ensuring continuity in mathematical functions.

This approach can be applied to other functions where continuity is desired at certain points.

Understanding the behavior of functions at undefined points is crucial for their proper analysis and manipulation.

The concept of division by zero and its implications in function definitions is a fundamental aspect of algebra.

The ability to identify and address discontinuities in functions is an essential skill in mathematics.

This example illustrates the importance of constraints in function definitions to maintain their validity and continuity.

The process of simplifying a function can reveal insights into its behavior and potential areas of discontinuity.

The redefinition of f(x) at x = -2 to achieve continuity showcases the adaptability of mathematical functions to meet specific criteria.

Transcripts

Browse More Related Video

Limits by factoring | Limits and continuity | AP Calculus AB | Khan Academy

Finding Derivative Using Limit Definition

2019 AP Calculus AB Free Response Question #6

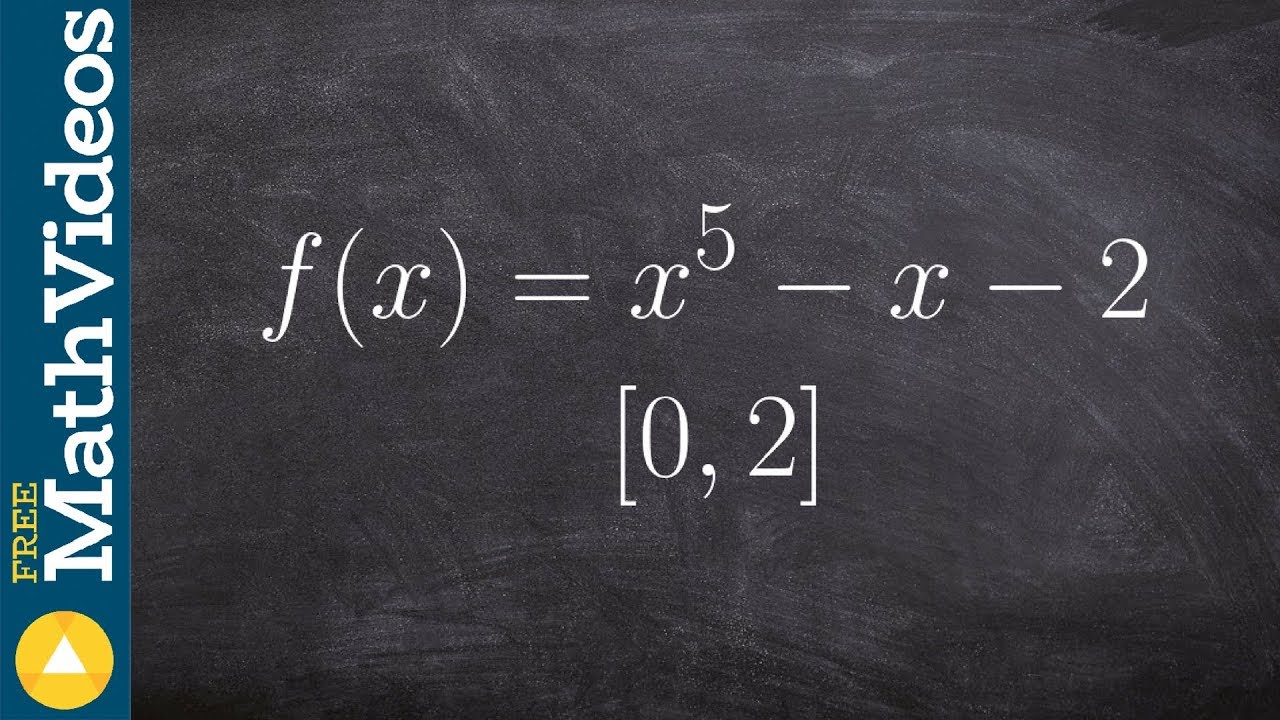
How to show that a solution exists to a functions using IVT

2019 AP Calculus AB FRQ #6

Absolute Maximum and Minimum Values - Finding absolute MAX & MIN of Functions - Calculus

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Function ContinuityMathematical AnalysisUndefined PointsRedefining FunctionsAlgebraic SimplificationFactoring TechniquesDenominator IssuesContinuous RedefinitionMath EducationProblem Solving