2011 Calculus AB Free Response #1 parts b c d | AP Calculus AB | Khan Academy

Khan Academy
8 Sept 201114:37
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses the concept of average velocity, emphasizing its relationship with distance and time. It explains that average velocity is the total distance traveled divided by the time taken, and without a specific position function, one must utilize the velocity function to calculate the distance. The method involves approximating the area under the velocity curve from time 0 to 6 as the total distance traveled. The script highlights the use of a calculator, specifically the TI-85, to evaluate the definite integral of the velocity function over the given time interval. The process is clear and informative, providing a practical approach to understanding and calculating average velocity in physics.

Takeaways
  • 📝 The concept of average velocity is introduced as the total distance traveled divided by the time taken.
  • 🔢 To calculate average velocity, use the formula: average velocity = distance / time.
  • 📈 The distance traveled can be determined by calculating the area under the velocity-time graph.
  • 🏷️ The symbol 'd' or 's' is sometimes used to represent distance or displacement in calculations.
  • 🌟 For small time intervals, the product of time and the constant velocity during that interval approximates the distance traveled.
  • 🧩 The total distance over a period is the sum of the distances of all small time intervals, represented by the area under the curve.
  • 📊 The definite integral of the velocity function 'v(t)' from 0 to 6 represents the total distance traveled from time 0 to time 6.
  • 📱 The use of calculators, such as the TI-85, is allowed and recommended for evaluating complex definite integrals.
  • 🛠️ The process of finding the average velocity involves first determining the distance traveled and then dividing by the total time of travel (in this case, 6 units).
  • 📱 The script briefly mentions navigating to the catalog function on the TI-85 calculator to evaluate definite integrals.
Q & A

  • What is the definition of average velocity?

    -Average velocity is defined as the total distance traveled divided by the total time taken.

  • How can you represent distance or displacement in mathematical terms?

    -You can represent distance or displacement with the variable 'd' or 's' in mathematical terms.

  • What is the relationship between distance, average velocity, and time?

    -The relationship between distance (d), average velocity (v), and time (t) is given by the formula: d = v * t.

  • Why is the position function not explicitly given in this problem?

    -The position function is not given because the focus is on finding the average velocity using the velocity function, which is provided.

  • How can you estimate the distance traveled during a small time interval?

    -You can estimate the distance traveled during a small time interval by multiplying the time by the constant velocity over that interval, which gives you the area of a small column representing the distance traveled.

  • What is the method to calculate the total distance traveled between time 0 and time 6?

    -The total distance traveled between time 0 and time 6 is calculated using the definite integral of the velocity function (v(t)) from 0 to 6.

  • How do you find the average velocity given the total distance and elapsed time?

    -To find the average velocity, divide the total distance (found from the definite integral of the velocity function) by the elapsed time.

  • What tool is mentioned for evaluating the definite integral in this problem?

    -A calculator, specifically the TI-85, is mentioned as a tool for evaluating the definite integral in this problem.

  • What is the purpose of the catalog function on the TI-85 calculator?

    -The catalog function on the TI-85 calculator provides a list of different mathematical functions available for use, including those for evaluating definite integrals.

  • What is the change in time (delta t) in this problem?

    -The change in time (delta t) in this problem is 6, as the time interval considered is from 0 to 6.

  • How does the process of finding the average velocity involve the velocity function?

    -The process involves first finding the total distance traveled by calculating the area under the velocity function curve from time 0 to 6 using definite integration, and then dividing that distance by the elapsed time to find the average velocity.

Outlines
00:00
📝 Calculation of Average Velocity

The paragraph introduces the concept of average velocity and explains its relationship with distance and time. It emphasizes that average velocity is the total distance traveled divided by the total time taken. The explanation includes a discussion on how to calculate the distance when the position function is not given by using the velocity function and the concept of integration. The process of finding the area under the curve from time 0 to 6 is described as a method to determine the total distance traveled. The paragraph also mentions the use of calculators, specifically the TI-85, to evaluate the definite integral which represents the distance in this context.

Mindmap
Keywords
💡average velocity
Average velocity is a measure of the rate at which an object covers distance over a given time period. In the context of the video, it is calculated by dividing the total distance traveled by the time interval. The script mentions that average velocity equals the distance traveled divided by time, and this concept is central to solving the problem presented, which involves finding the average velocity of a particle between two specific times.
💡distance
Distance refers to the total length of the path taken by an object in motion. In the video, the distance traveled by the particle between time 0 and time 6 is the focus, and it is determined by calculating the area under the velocity curve over that time span. The script emphasizes that distance is the integral of the velocity function over the given time interval, which is essential for finding the average velocity.
💡displacement
Displacement is the straight-line distance between the starting and ending points of an object's path and is a vector quantity, meaning it has both magnitude and direction. Although not explicitly mentioned in the script, displacement is related to the concept of distance and would be the same in a one-dimensional motion without any change in direction. The video focuses on calculating the distance, which in a straight-line scenario would be equivalent to displacement.
💡velocity function
A velocity function, denoted as v(t) in the script, is a mathematical representation that describes the velocity of an object as a function of time. The shape of this function can indicate how the speed of the object changes over time. In the video, the velocity function is crucial for determining the area under the curve, which represents the total distance traveled by the particle during the specified time period.
💡definite integral
A definite integral is a mathematical operation that calculates the area under a curve over a specified interval. In the context of the video, the definite integral of the velocity function from time 0 to time 6 is used to find the total distance traveled by the particle. The script emphasizes that this integral is key to solving for the average velocity, as it provides the necessary distance information.
💡time interval
A time interval refers to the difference in time between two points. In the video, the time interval is from time 0 to time 6, which is the period over which the average velocity is to be calculated. Understanding the time interval is crucial for determining the limits of integration when calculating the definite integral of the velocity function.
💡area under the curve
The area under the curve of a function represents the accumulated value over the interval of interest. In the script, the area under the velocity curve between times 0 and 6 is used to determine the total distance traveled by the particle. This concept is central to the problem-solving process as it relates directly to the calculation of average velocity.
💡constant velocity
Constant velocity implies that an object moves at a steady pace without acceleration. In the video, the script suggests multiplying a small time interval by the constant velocity to estimate the distance traveled during that interval. This simplification is used to approximate the area under the curve and estimate the total distance traveled by the particle.
💡calculator
A calculator is an electronic device used to perform mathematical calculations. In the context of the video, the use of a calculator, specifically the TI-85, is mentioned to evaluate the definite integral analytically. This tool is essential for solving the problem as it allows for the numerical integration of the velocity function over the specified time interval.
💡catalog
In the context of the video, the catalog refers to the menu or list of functions available on the TI-85 calculator. The script mentions going to the catalog to find the function for evaluating definite integrals, which is an important step in the process of calculating the average velocity of the particle.
💡position function
A position function describes the position of an object as a function of time. Although not explicitly mentioned in the script, the position function would be related to the velocity function and could be used to determine the distance traveled if it were provided. The video focuses on using the velocity function to calculate the distance and average velocity instead.
Highlights

Introduction to the concept of average velocity.

Explanation that distance equals average velocity times time.

Clarification on the absence of an explicit position function.

Use of velocity function to infer distance traveled.

Description of the method to calculate distance as the area under the curve.

Application of definite integral to represent the total distance.

Mention of the use of calculators for evaluating integrals.

Procedure to find the distance traveled between time 0 and 6.

Reference to the TI-85 calculator and its functions.

Explanation of navigating the TI-85 calculator's catalog.

Use of the definite integral function on the calculator.

The process of dividing the calculated distance by time to find average velocity.

Emphasis on the importance of time interval in the calculation.

General drawing of the velocity function for illustrative purposes.

Transcripts

Browse More Related Video

Definite integrals (part II)

Area under rate function gives the net change | AP Calculus AB | Khan Academy

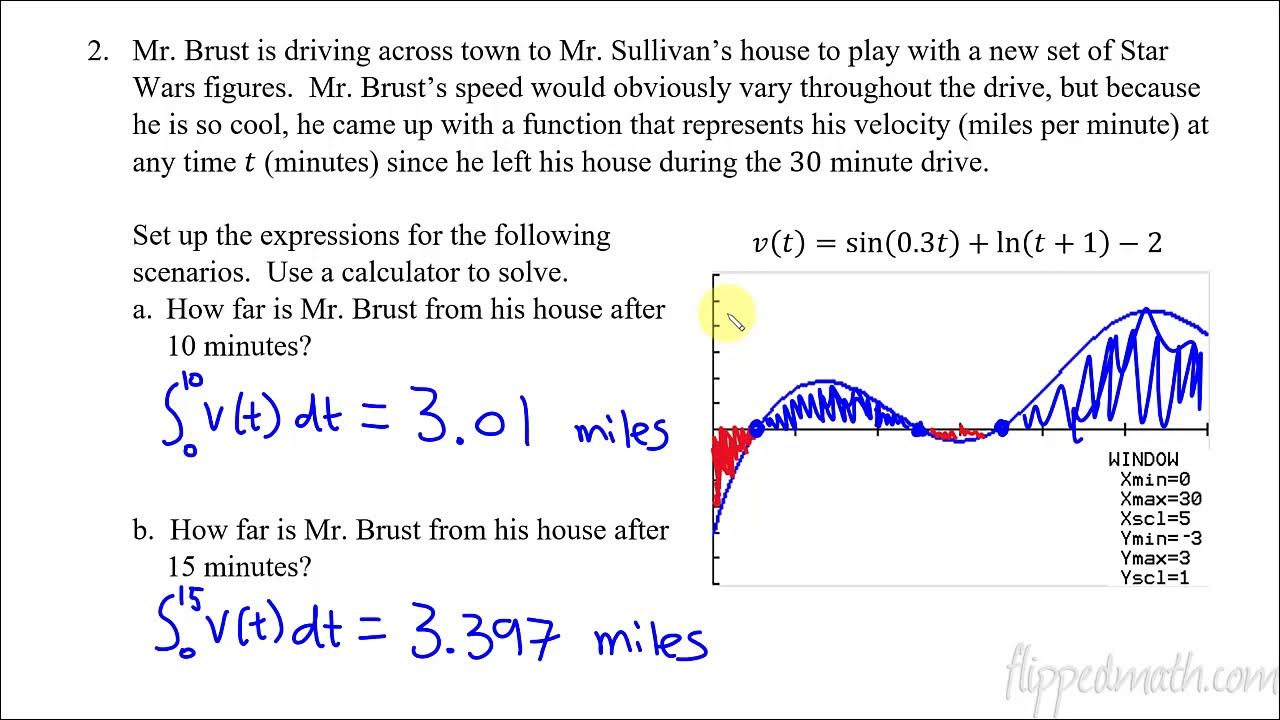
Calculus AB/BC – 8.2 Connecting Position, Velocity, and Acceleration of Functions Using Integrals

GCSE Physics - Velocity Time Graphs #54

Definite Integrals (area under a curve) (part III)

Average velocity for constant acceleration | One-dimensional motion | Physics | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Physics ConceptsAverage VelocityIntegral CalculusMotion AnalysisEducational ContentMathematical ApproachTI-85 CalculatorTime IntervalDistance Calculation