Exponential Growth
TLDRThe video script discusses the concept of exponential growth using the analogy of a bacteria culture. It explains how to derive an expression for the number of bacteria after a certain period, given the initial count and the growth rate. The script provides a step-by-step guide on solving for the growth constant 'k' and the initial condition 'I naught', and then uses these to find the bacteria population after 3 hours. It also covers how to calculate the rate of growth at a specific time and concludes with determining the time it takes for the population to reach a milestone of 10,000. The problem is analogous to compound interest, highlighting the principle of growth being proportional to the current size.
Takeaways
- 📈 The problem discussed is about exponential growth, analogous to compound interest calculations with the mathematical constant e.
- 🦠 The bacteria culture starts with 100 cells and grows proportionally to its size, with the population reaching 420 after one hour.
- 🔍 The general form of an exponential growth function is b(t) = I₀ * e^(kt), where I₀ is the initial amount and k is the growth rate.
- 🧠 To find I₀ (initial number of bacteria), the script uses the fact that at t=0, b(0) should equal 100 cells.
- 🔢 By using the given data point after one hour, the script calculates the growth rate k as ln(4.2) by setting up the equation 420 = 100 * e^(k) and solving for k.
- 📊 The exponential growth function for the bacteria is then b(t) = 100 * 4.2^t, derived from the initial conditions and the calculated growth rate.
- 🕒 To find the number of bacteria after 3 hours, the script substitutes t=3 into the exponential growth function, yielding 100 * (4.2^3).
- 🚀 The rate of growth after 3 hours is found by taking the derivative of the growth function with respect to time, resulting in b'(t) = 100 * ln(4.2) * 4.2^t.
- 🎯 The time when the population reaches 10,000 is determined by setting b(t) to 10,000 and solving for t, which simplifies to t = ln(100) / ln(4.2).
- 🌟 The concept of exponential growth can be applied to various scenarios, such as bank account interest, demonstrating the principle of growth being proportional to the current size.
Q & A
What is the main topic of the video script?
-The main topic of the video script is exponential growth, specifically as it applies to a bacteria culture growing over time.
How does the bacteria culture initially contain bacteria cells?
-The bacteria culture initially contains 100 cells.
What is the rate of growth mentioned in the script?
-The rate of growth mentioned is proportional to the size of the bacteria culture.
What is the population of the bacteria culture after one hour?
-After one hour, the population of the bacteria culture has increased to 420.
What is the general form of the equation for exponential growth?
-The general form of the equation for exponential growth is b(t) = I_naught * e^(kt), where I_naught is the initial amount, k is the growth rate, and t is time.
How is the value of k determined in the script?
-The value of k is determined by using the given data point where the population is 420 after one hour, and solving the equation 420 = 100 * e^(k*1) for k, which results in k being equal to the natural log of 4.2.
What is the function for the number of bacteria after t hours?
-The function for the number of bacteria after t hours is b(t) = 100 * 4.2^t, derived from the initial condition and the growth rate k.
How many bacteria are there after 3 hours according to the script?
-After 3 hours, there are approximately 70,148 bacteria, calculated by using the function b(t) = 100 * 4.2^t and substituting t with 3.
What is the rate of growth of the bacteria culture after 3 hours?
-The rate of growth after 3 hours is found by taking the derivative of the bacteria function with respect to time, which results in b'(t) = 100 * ln(4.2) * 4.2^t. When t equals 3, this simplifies to 4.2^3, which is approximately 70,148 bacteria per hour.
How is the population of 10,000 bacteria reached?
-The population of 10,000 bacteria is reached when t equals to ln(100) / ln(4.2). By plugging this into a calculator, one can find the time it takes for the bacteria culture to reach 10,000.
What is the significance of the natural log in this script?
-The natural log is used to solve for the growth rate k and to find the time when the population reaches a certain number. It is a fundamental part of the calculations for exponential growth.
How can the concepts from the script be applied to a different context?
-The concepts from the script can be applied to any scenario involving exponential growth or decay, such as a bank account growing through compound interest.
Outlines
📈 Introduction to Exponential Growth Problem
The video begins with an introduction to solving a problem related to exponential growth, using a bacteria culture as an analogy to compound interest. The initial condition states that the bacteria culture starts with 100 cells, and the growth rate is proportional to its size. The goal is to find an expression for the number of bacteria after t hours, denoted as b(t). The presenter draws an analogy with the number e in compound interest scenarios and establishes the general form of the exponential growth equation, which is b(t) = I₀ * e^(kt), where I₀ is the initial amount and k is the growth rate. The problem provides a data point that after one hour, the population increases to 420, which will be used to solve for the unknown variable k.
🧬 Deriving the Growth Rate Constant (k)
In this segment, the presenter focuses on determining the growth rate constant (k) by using the given data point where the population reaches 420 after one hour. By substituting the values into the exponential growth equation, the presenter solves for k by dividing the final population (420) by the initial population (100) and taking the natural log of the result, finding that e^(k) equals 4.2. The presenter then explains the process of finding the number of bacteria after 3 hours by plugging the value of t into the derived exponential growth function. Additionally, the presenter introduces the concept of the derivative to find the rate of growth at a specific time, in this case, after 3 hours.
📊 Calculating Bacterial Growth After 3 Hours
This part of the video script details the calculation of the bacterial population after 3 hours using the derived exponential growth function. The presenter simplifies the exponential function to b(t) = 100 * 4.2^t and calculates the population by substituting t with 3. The presenter also explains the concept of the natural log and its application in simplifying the exponential function. Furthermore, the presenter derives the rate of growth function, b'(t), by differentiating the bacterial population function with respect to time, resulting in b'(t) = 100 * ln(4.2) * 4.2^t. The explanation includes a simplification of the derivative function and emphasizes the importance of understanding logarithms and derivatives in solving such problems.
🕰️ Determining Time to Reach a Population Milestone
The final paragraph addresses the question of when the bacterial population will reach 10,000. The presenter revisits the exponential growth equation, now in the simplified form of b(t) = 100 * 4.2^t, and sets it equal to 10,000 to find the time t at which this population milestone is achieved. By taking natural logs and manipulating the equation, the presenter arrives at a formula for calculating t. The explanation includes alternative methods for solving logarithmic equations and emphasizes the practicality of using different bases in logarithms. The presenter concludes by noting the applicability of the concepts learned to other scenarios, such as compound interest, and mentions the intention to cover more problems and topics, including exponential decay, in future videos.
Mindmap
Keywords
💡Exponential Growth
💡Bacteria Culture
💡Initial Number
💡Rate of Growth
💡Compound Interest
💡Natural Logarithm
💡Derivative
💡Chain Rule
💡Logarithm Properties
💡Time Variable (t)
💡Population Threshold
Highlights
The problem discussed is an exponential growth problem, analogous to compound interest, involving a bacteria culture.
The bacteria culture initially contains 100 cells and grows at a rate proportional to its size.
After one hour, the population of bacteria increases to 420.
The general form of the equation for exponential growth is the initial amount times e to the power of kt, where k is the growth rate.
The initial number of bacteria (I naught) is given as 100 cells.
By using the given data points, one can solve for the growth rate constant k, which is found to be ln(4.2).
The function for the number of bacteria after t hours is b(t) = 100 * e^(kt), with k being ln(4.2).
The number of bacteria after 3 hours can be found by substituting t = 3 into the growth function.
The rate of growth after 3 hours is determined by taking the derivative of the bacteria function with respect to time.
The derivative at any time t is b'(t) = 100 * ln(4.2) * e^(ln(4.2)t), which simplifies to 100 * ln(4.2) * 4.2^t.
The population will reach 10,000 when b(t) equals 10,000, which can be solved by setting 100 * e^(ln(4.2)t) equal to 10,000 and solving for t.
The time it takes for the population to reach 10,000 can be found by taking the natural log of both sides of the equation and solving for t.
The problem can be applied to other contexts such as compound interest by replacing bacteria with money.
The concept of exponential growth demonstrates that as the population grows, the absolute increase per unit of time also increases.
The problem can be solved using logarithm properties, showcasing the importance of understanding different bases and how to convert between them.
The transcript provides a comprehensive walkthrough of solving an exponential growth problem, from identifying initial conditions to calculating derivatives and solving for specific future values.
The analogy between bacteria growth and compound interest illustrates the broader applicability of exponential growth models in various fields.
The use of natural logs and exponentiation is emphasized as a key mathematical tool for solving exponential growth problems.
The transcript concludes with a promise to cover more problems and topics, including exponential decay, to reinforce understanding.
Transcripts
Browse More Related Video
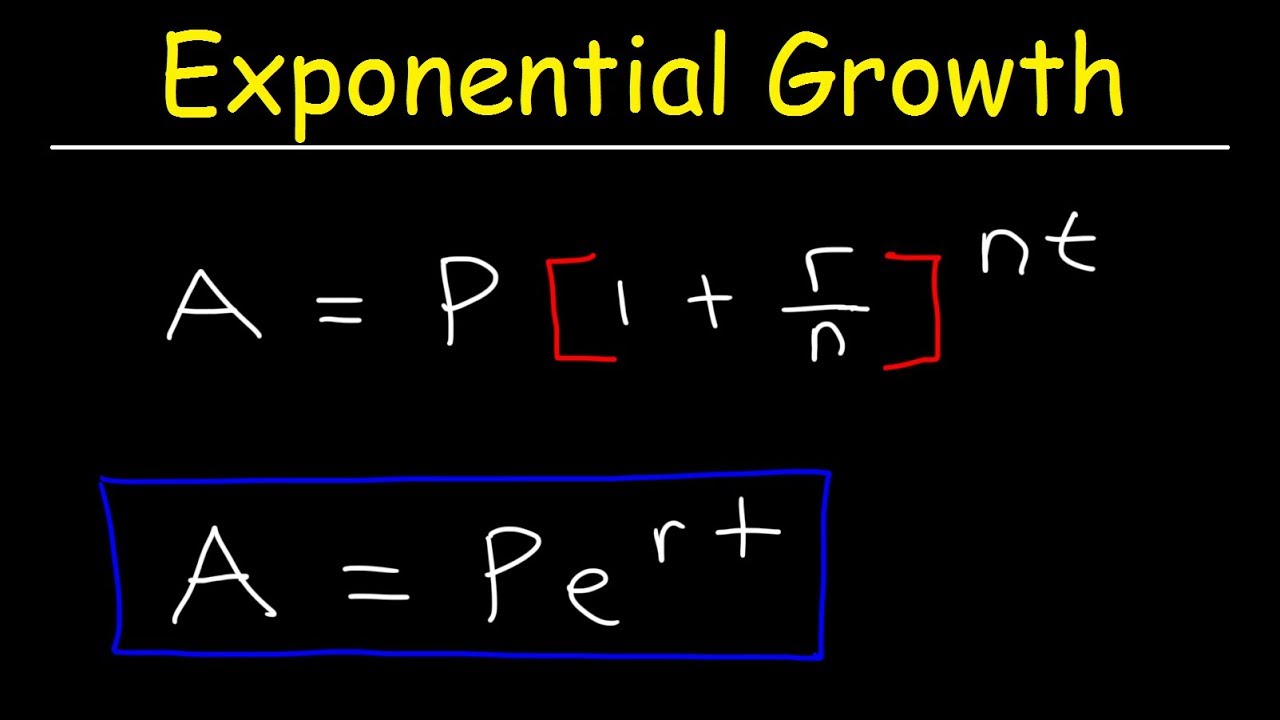
Compound Interest & Population Growth Word Problems - Logarithms

Exponential Growth and Decay Calculus Problem Solution | How To Find Relative Growth Rate
Math 11 - Section 2.4 (previously section 3.3)

Exponential Growth and Decay Calculus, Relative Growth Rate, Differential Equations, Word Problems

Exponential Growth and Decay (Precalculus - College Algebra 66)
Exponential Growth and Decay Word Problems & Functions - Algebra & Precalculus
5.0 / 5 (0 votes)
Thanks for rating: