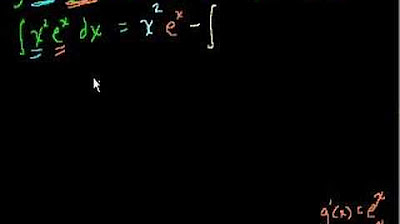Indefinite Integration (part 7)
TLDRThe video script presents a detailed walkthrough of solving a classic integration by parts problem involving e^x and cosine x. The speaker skillfully demonstrates how the properties of these functions, which cycle upon differentiation and integration, allow for the problem to be restated without actually computing the integral. The final solution is elegantly expressed as the average of e^x times cosine x and e^x times sine x, divided by 2, emphasizing the beauty and utility of integration by parts in calculus.
Takeaways
- 📚 The speaker is about to solve an integration by parts problem, which they find fun and classic.
- 🌟 The problem involves integrating e^x times cosine of x, a common example used in math education and competitions.
- 🔄 The speaker emphasizes the cyclical nature of the functions involved, such as e^x and cosine x, in terms of differentiation and integration.
- 📈 The process of integration by parts is applied twice, showcasing how it can be used to simplify complex integrals.
- 🎓 The speaker humorously refers to their high school days as a 'mathlete', indicating a strong interest in mathematics from a young age.
- 🤔 The problem is solved without actually evaluating the final integral, demonstrating a clever trick in calculus.
- 📊 The final result is expressed as the average of e^x times cosine of x and e^x times sine of x, which is a neat property and solution.
- 💡 The speaker encourages the audience to appreciate the beauty of mathematics and to explore the concepts further, such as by graphing the functions.
- 📝 The importance of including the constant 'c' in anti-derivatives is mentioned, highlighting attention to detail in mathematical solutions.
- 🌐 The presentation aims to instill a love for mathematics in the audience, showing the potential for enjoyment in problem-solving.
Q & A
What is the main topic of the video?
-The main topic of the video is solving integration by parts problems, specifically focusing on the integral of e^x times cosine of x.
Why does the speaker refer to integration by parts as a 'fun problem'?
-The speaker refers to it as a 'fun problem' because it involves classic functions like e^x and cosine of x, which have interesting properties when taking derivatives and anti-derivatives, and it demonstrates the process of integration by parts without needing to evaluate the final integral.
What is the significance of e^x in the context of integration by parts?
-In the context of integration by parts, e^x is significant because it remains unchanged when taking derivatives or anti-derivatives, making it a convenient function to use in the integration by parts formula.
How does the speaker initially set up the integration by parts formula?
-The speaker initially sets up the integration by parts formula by assuming e^x as g'(x) and cosine of x as f(x), then applying the formula which states that the integral of g'(x)f(x) is g(x)f(x) minus the integral of g(x)f'(x).
What is the derivative of cosine of x?
-The derivative of cosine of x is minus sine of x.
How does the speaker use the properties of cosine and sine functions in the solution?
-The speaker uses the properties of cosine and sine functions, which cycle through certain values when derivatives are taken repeatedly, to simplify the integral and eventually solve it without directly evaluating the final integral.
What is the final result of the integral of e^x times cosine of x?
-The final result of the integral of e^x times cosine of x is e^x times cosine of x plus e^x times sine of x divided by 2.
Why does the speaker suggest graphing the solution?
-The speaker suggests graphing the solution to visually understand the relationship between e^x, cosine of x, and sine of x, and to appreciate the neat property that the integral represents the average of e^x times cosine of x and e^x times sine of x.
What is the significance of the 'plus c' in the final answer?
-The 'plus c' in the final answer is a reminder that the constant of integration is omitted in the provided solution. Including the constant is crucial for a complete and accurate anti-derivative.
How does the video demonstrate the power of integration by parts?
-The video demonstrates the power of integration by parts by showing how it can be used to simplify and solve complex integrals without directly evaluating them, and by illustrating how the process can reveal interesting mathematical properties and relationships.
Outlines
📚 Introduction to Integration by Parts
The speaker begins by expressing enthusiasm for tackling integration by parts problems, highlighting their popularity and potential complexity. The chosen problem integrates e^x times cosine x, a classic example often used in math education and competitions. The speaker explains the unique properties of e^x and cosine x, emphasizing their cyclical nature when it comes to differentiation and integration. The process of integration by parts is introduced, with e^x assumed to be g'(x) and the focus on how it cycles between its derivative and anti-derivative. The speaker then outlines the steps of integration by parts, substituting the functions accordingly and simplifying the integral expression.
🔄 Solving the Integral Using Integration by Parts
The speaker continues the discussion by applying integration by parts to the problem at hand. After the initial application, the speaker notes that the result is still an integral of a similar form, prompting a second use of integration by parts. The process is detailed, with the speaker carefully explaining each step, including the anti-derivatives and derivatives of the functions involved. The speaker then cleverly rearranges the equation and highlights a key insight: the equation can be simplified by adding a term to both sides, effectively canceling out parts and leading to a solution. The integral of e^x times cosine x is shown to be the average of e^x times cosine x and e^x times sine x, divided by 2. The speaker concludes by emphasizing the elegance of the solution and encourages further exploration of the functions involved.
Mindmap
Keywords
💡Integration by Parts
💡e^x
💡Cosine x
💡Derivative
💡Anti-derivative
💡Mathlete
💡Classic Problem
💡Trigonometric Functions
💡Indefinite Integral
💡Sine x
💡Cycle
Highlights
The speaker introduces integration by parts problems as a fun and classic topic in mathematics.
Integration by parts is often used as an example in math classes and competitions, and can be seen as a trick problem.
The problem discussed involves integrating e to the power of x times cosine of x, a classic example in integration by parts.
The properties of e to the x and cosine of x make this problem interesting, as they cycle through derivatives and anti-derivatives.
The speaker explains the process of integration by parts, using e to the x as an example of a function that remains unchanged through derivatives and anti-derivatives.
The derivative of cosine of x is minus sine of x, which is used in the integration by parts process.
The speaker demonstrates the integration by parts formula: ∫u dv = uv - ∫v du.
The problem is solved without evaluating the final integral, showcasing the power of integration by parts.
The integral of e to the x cosine of x is shown to be equal to e to the x cosine of x plus the integral of e to the x sine of x.
The speaker uses integration by parts twice, starting with e to the x cosine of x and ending up with a simpler expression.
The final solution is obtained by adding a term to both sides of the equation and dividing by 2.
The integral is solved by recognizing a pattern in the results and simplifying the expression.
The solution involves the average of e to the x cosine of x and e to the x sine of x, which is a neat property.
The speaker emphasizes the importance of understanding the cyclical nature of certain functions in solving integration by parts problems.
The presentation concludes with the speaker encouraging the audience to explore the graph and properties of the solved functions.
The speaker's approach to the problem demonstrates a deep understanding of calculus and its applications.
The transcript serves as an educational resource for those interested in learning about integration by parts and its applications.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: