Derivatives with Multiple Rules
TLDRThe video script is a detailed walkthrough of deriving various mathematical functions using calculus rules. It emphasizes the importance of identifying the 'big picture' rule, such as the chain rule or product rule, before delving into the specifics of each function. The presenter guides through three different functions, illustrating how to apply the quotient rule, chain rule, and product rule, often within a nested structure where one rule leads to the application of another. The process involves taking derivatives of both the outer and inner functions, multiplying these results, and handling cases where the derivative of a constant is zero. The script is instructional, aiming to equip viewers with a clear method for tackling complex derivative problems by stacking different calculus rules as needed.
Takeaways
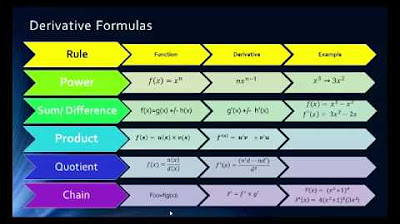
- 📚 First, identify the 'big picture rule' for the function you're differentiating, such as the chain rule or product rule.
- 🔍 When differentiating a function, start with the derivative of the outside of the expression first.
- 🧐 Pay attention to any nested expressions, as they may require additional rules like the quotient rule.
- 🔑 Use the chain rule when differentiating composite functions, bringing down the power and copying the inner expression.
- 📈 For a function raised to a power, the power rule involves multiplying the derivative by the original function.
- 🤔 Consider algebraic simplifications that might make the differentiation process easier, such as factoring out common terms.
- 📝 When applying the product rule, remember it involves differentiating both the 'first' and 'second' parts of the product and then combining them.
- 🔄 If a derivative within a rule requires another rule (like the chain rule within the product rule), apply the necessary rule step by step.
- ✅ Always multiply the derivatives of the outer and inner functions when using the chain rule or product rule.
- 📊 For functions with multiple terms, treat each term as a separate entity when applying the product rule.
- 📋 Keep in mind that constants within expressions have a derivative of zero, as they do not change the value of the function.
Q & A
What is the first function discussed in the transcript?
-The first function discussed is f(x) = (4x^2 - 5) / (2 - x)^3.
What are the two main rules mentioned for finding the derivative of the first function?
-The two main rules mentioned are the chain rule and the quotient rule.
How does the speaker approach the derivative of the outside of the first function?
-The speaker applies the chain rule to the outside of the function by taking the derivative of (2 - x)^3 three times.
What is the process for finding the derivative of the inside of the first function?
-The process involves applying the quotient rule after taking the derivative of the numerator (4x^2 - 5) and the denominator (2 - x) separately.
What is the second function presented in the transcript?
-The second function is g(t) = (6 - t^2) * t^2 + 5t, all raised to the fourth power.
What rule is identified as the big picture rule for the second function?
-The big picture rule for the second function is the chain rule.
How does the speaker simplify the process of finding the derivative of the second function?
-The speaker simplifies the process by first applying the chain rule to the outside of the function and then dealing with the product rule within the chain rule.
What is the third function s(x) mentioned in the transcript?
-The third function is s(x) = (6x^4 + 5)^4 * (x^3 - 7x)^3.
What rule is identified as the big picture rule for the third function?
-The big picture rule for the third function is the product rule.
How does the speaker approach the derivative of the third function?
-The speaker approaches it by first applying the product rule and then using the chain rule within the derivative of the second part of the product.
What is the key takeaway from the transcript regarding the process of finding derivatives?
-The key takeaway is to first identify the big picture rule (chain rule, product rule, etc.), then apply it and be prepared to use additional rules as needed within that framework.
Why is it important to identify the big picture rule before starting to find the derivative?
-Identifying the big picture rule helps to structure the problem-solving approach and ensures that you apply the correct method from the start, making the process more efficient and less prone to errors.
Outlines
📚 Deriving Functions with Chain and Quotient Rules
The speaker begins by addressing the audience and stating their intention to cover the final examples in section 9.7. They emphasize the importance of identifying the 'big picture rule' for derivatives, which in this case is the chain rule due to the cubing of the entire expression. The function f(x) is given, and the process of differentiating it involves applying the chain rule and the quotient rule. The derivative of the outer function is calculated first, followed by the derivative of the inner function. The process is explained step by step, highlighting the need for the quotient rule when differentiating the inner function. The final derivative is obtained by substituting the derived expressions back into the original function.
🔢 Applying Chain and Product Rules for Derivatives
The speaker continues with the second function, g(t), which is a more complex expression involving a power rule and a product rule. They clarify that algebraic manipulations, while possible, do not necessarily simplify the differentiation process. The main strategy is to identify the overarching rule, which is the chain rule, and then to recognize that the derivative of the inner function will require a product rule. The derivative of the outer function is calculated by bringing down the power and copying the inner function, which is then cubed. The inner function's derivative is found by applying the product rule to its components. The process is detailed, showing the application of both the chain rule and the product rule within the given expression.
🔍 Complex Derivatives with Multiple Rules
The final paragraph discusses the function s(x), which is even more complex and requires both a product rule and multiple chain rules. The speaker advises the audience to think about the 'big picture rule' and then to apply it, being prepared to use additional rules as needed within that framework. The function involves several terms, each raised to a power, and the differentiation process involves applying the product rule to the outer function and then the chain rule to the inner functions. The speaker demonstrates how to calculate the derivatives of each part of the expression and then how to combine them to obtain the final derivative. They assure the audience that they do not need to simplify the expressions for tests, as long as they apply the correct rules.
Mindmap
Keywords
💡Derivative
💡Chain Rule
💡Quotient Rule
💡Product Rule
💡Power Rule
💡Composite Function
💡Differentiation
💡Function
💡Rule of Differentiation
💡Algebraic Manipulation
💡Dance Partner
Highlights
Deriving functions involves identifying the big picture rule, such as the chain rule or quotient rule, to guide the process.
For the function f(x) = (4x^2 - 5) / (2 - x)^3, the chain rule is the primary approach with the quotient rule as a secondary step.
When applying the chain rule, first take the derivative of the outer function and then multiply by the derivative of the inner function.
For the function g(t) = (6 - t^2) * t^2 + 5t)^4, a combination of chain rule and product rule is used in the derivation process.
The derivative of the inner function within g(t) requires the use of the product rule due to the multiplication of two expressions.
When faced with a function like s(x) = (6x^4 + 5)^4 * x^3 - 7x^3, the product rule is the overarching strategy with nested chain rules.
In the case of s(x), the derivative of the outer function involves a power rule, which then requires a chain rule for the inner function.
The process of differentiating complex functions involves stacking rules, such as chain rule followed by product rule, and vice versa.
For s(x), the derivative of the first part requires a chain rule, and the derivative of the second part involves another application of the chain rule.
When differentiating, it's important to recognize when a quotient rule is necessary, as seen when differentiating the function f(x).
The derivative of the inner function in g(t) involves the product rule, which includes the derivatives of each multiplied term.
The process of finding derivatives can be simplified by focusing on the big picture rule and then applying any necessary secondary rules.
In the transcript, the speaker emphasizes the importance of recognizing the primary rule for differentiation before moving on to secondary rules.
The speaker provides a step-by-step guide on how to approach the differentiation of complex functions with multiple rules.
The transcript demonstrates the application of calculus rules in a practical and educational manner, making it easier to understand the process of differentiation.
The speaker uses a conversational tone to explain complex mathematical concepts, which may help in making the material more accessible to learners.
The process of differentiation is shown to be iterative, where one rule may lead to the need for another, requiring a sequential application of rules.
The transcript serves as a valuable resource for understanding the mechanics of differentiation, particularly when multiple rules are involved.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: