Visualizing the chain rule and product rule | Chapter 4, Essence of calculus
TLDRThis video script delves into the concept of derivatives for more complex functions, emphasizing the importance of understanding rather than memorizing the rules. It breaks down the process into three fundamental ways to combine functions: addition, multiplication, and composition. The script provides clear examples and visualizations to explain the sum rule, product rule, and chain rule, illustrating how each rule arises naturally from the concept of derivatives. The aim is to equip viewers with the tools to tackle any complex function by understanding the underlying patterns and principles.
Takeaways
- 📚 The script discusses the derivation of more complex functions by combining simple ones, emphasizing understanding over memorization.
- 🔍 Three fundamental ways to combine functions are identified: addition, multiplication, and composition (one function inside another).
- 📈 The sum rule for derivatives is straightforward: the derivative of the sum is the sum of the derivatives.
- 🤔 The product rule is more complex, involving the derivative of one function times the other function, plus the other function times the derivative of the first.
- 📐 The chain rule is introduced for function composition, where the derivative of the outer function times the derivative of the inner function gives the result.
- 📉 The script uses the example of \( f(x) = \sin(x) + x^2 \) to illustrate the sum rule and the concept of taking derivatives.
- 📐 The product rule is explained with the mnemonic 'left d right, right d left', helping to remember the order of operations for derivatives of products.
- 📊 The chain rule is demonstrated with the composition of functions, such as \( \sin(x^2) \), and the importance of understanding the intermediate steps is highlighted.
- 📘 The importance of visualizing derivatives, such as through the adjustable box analogy for products, is emphasized for better understanding.
- 🔢 The script clarifies that constants multiplied by functions have derivatives that are simply the constant times the derivative of the function.
- 💪 The necessity of practice for fluency in applying calculus rules is stressed, as understanding the rules' origins is not enough for mastery.
Q & A
What is the main goal of understanding derivatives of simple functions before moving on to more complex ones?
-The main goal is to develop a clear picture or intuition that explains where the formulas for derivatives come from, which serves as a foundation for understanding more complex derivatives.
How many basic ways are there to combine functions when taking derivatives, according to the script?
-There are three basic ways to combine functions: addition, multiplication, and composition (throwing one function inside the other).
What is the sum rule for derivatives and how is it applied?
-The sum rule states that the derivative of a sum of two functions is the sum of their derivatives. It's applied by taking the derivative of each function separately and then adding the results together.
Can you provide an example of how the sum rule is applied to a function?
-An example given in the script is the function f(x) = sin(x) + x^2. The derivative is found by taking the derivative of sin(x), which is cos(x), and the derivative of x^2, which is 2x, and then adding them to get f'(x) = cos(x) + 2x.
Why is the product rule more complex than the sum rule?
-The product rule is more complex because it involves considering the changes in both the width and height of an 'adjustable box' representing the product of two functions, which leads to three different areas of change that need to be accounted for.
What is the mnemonic 'Left d right, right d left' and how does it relate to the product rule?
-The mnemonic 'Left d right, right d left' is a way to remember the product rule. It means to take the derivative of the left function and multiply it by the original right function, and then add the derivative of the right function multiplied by the original left function.
How does the chain rule differ from the sum and product rules?
-The chain rule is used for function composition, where one function is inside another. It involves taking the derivative of the outer function evaluated at the inner function and multiplying it by the derivative of the inner function.
Can you explain the chain rule with an example from the script?
-The example given is the function g(h(x)) = sin(x^2). The derivative is found by taking the derivative of the outer function sin(h), which is cos(h), and multiplying it by the derivative of the inner function x^2, which is 2x, resulting in the chain rule expression: d(sin(x^2))/dx = cos(x^2) * 2x.
What is the importance of understanding the intuition behind the derivative rules rather than just memorizing them?
-Understanding the intuition behind the rules allows for a deeper comprehension of derivatives, making it easier to apply these rules in various complex situations and to discover the patterns naturally through thoughtful consideration of what a derivative means.
What advice does the script give regarding practicing calculus mechanics?
-The script emphasizes that watching videos or learning the mechanics of calculus is not enough. It advises the viewer to practice the mechanics themselves to build the necessary skills and fluency in applying the rules.
Outlines
📚 Understanding Derivatives of Combined Functions
This paragraph introduces the concept of deriving more complex functions by combining simpler ones. It emphasizes the importance of understanding the origin of derivative formulas rather than just memorizing them. The speaker outlines three basic methods of combining functions: addition, multiplication, and composition. The paragraph also touches on the idea that subtraction and division of functions can be reduced to these basic operations. The focus then shifts to the sum rule for derivatives, which states that the derivative of a sum is the sum of the derivatives, using the function f(x) = sin(x) + x^2 as an example to illustrate the concept.
📐 Derivative of Products and the Product Rule
The second paragraph delves into the derivative of products of functions, highlighting the complexity compared to the sum rule. It uses the concept of an adjustable box to visualize the product of sine(x) and x^2 as an area, and explains how a small change in x (dx) affects this area. The paragraph introduces the product rule mnemonic 'left d right, right d left' to remember the formula for the derivative of a product of two functions, g(x)h(x), which is g'(x)h(x) + g(x)h'(x). It also mentions that multiplying by a constant simplifies the derivative to the constant times the derivative of the function.
🔗 The Chain Rule and Function Composition
This paragraph discusses the chain rule, which is essential for finding the derivative of a composition of functions. It uses the example of sine(x^2) to explain the process of visualizing the change in the output due to a small change in the input (dx). The paragraph describes the intermediate steps of changing x to x^2 (h) and then applying the sine function. It explains how the chain rule formula, g'(h(x))h'(x), is derived and emphasizes the importance of understanding the underlying process rather than just memorizing the formula.
💪 The Importance of Practice in Mastering Calculus
The final paragraph concludes the script by stressing the importance of practice in truly mastering the mechanics of calculus. It acknowledges the difference between knowing the rules and being able to apply them fluently in complex situations. The speaker encourages the viewer to seek out practice opportunities and reflects on the value of understanding the natural patterns and origins of calculus rules, rather than just memorizing them.
Mindmap
Keywords
💡Derivatives
💡Intuition
💡Combining Functions
💡Sum Rule
💡Product Rule
💡Function Composition
💡Chain Rule
💡Visualizing Derivatives
💡Mnemonic
💡Practicing Mechanics
Highlights
Derivatives of simple functions are foundational for understanding more complex functions in modeling.
Derivatives are intuitively understood by visualizing the effects of combining simple functions.
Three basic ways to combine functions are addition, multiplication, and composition.
Subtraction and division of functions can be reduced to addition and composition.
Understanding derivatives of combinations requires a step-by-step approach.
The sum rule for derivatives states that the derivative of a sum is the sum of derivatives.
Visualizing derivatives involves considering the change in function values with a small input adjustment.
The product rule for derivatives involves understanding the change in the 'area' of a product of two functions.
The mnemonic 'left d right, right d left' helps remember the product rule pattern.
Multiplying a function by a constant simplifies the derivative calculation.
Function composition involves understanding the change in an output due to an input change through an intermediary function.
The chain rule is essential for derivatives of composed functions and reflects the ratio of change through intermediate steps.
Visualizing derivatives through number lines can help understand the chain rule.
Derivatives of composed functions require understanding the proportionality constant between input and output changes.
The chain rule expression shows the ratio between a tiny change in the final output and the input change.
Practicing calculus mechanics is crucial for fluency and cannot be replaced by theoretical knowledge alone.
The rules for derivatives are not just to be memorized but are natural patterns discovered through understanding the meaning of a derivative.
Transcripts
Browse More Related Video

Product rule | Taking derivatives | Differential Calculus | Khan Academy
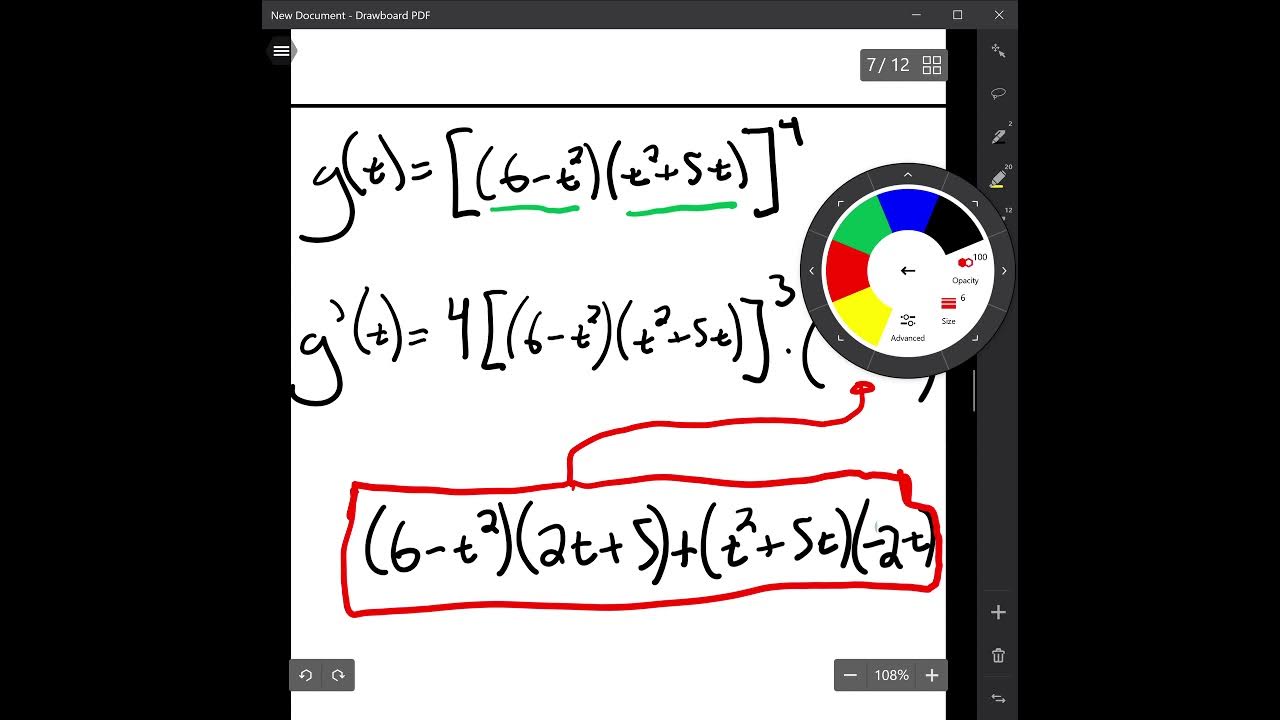
Derivatives with Multiple Rules

Derivatives of Composite Functions - Chain Rule, Product & Quotient Rule
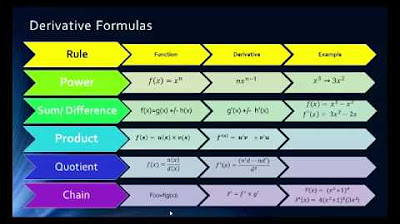
Math 1325 Lecture 9 7 - Using Derivative Forumulas
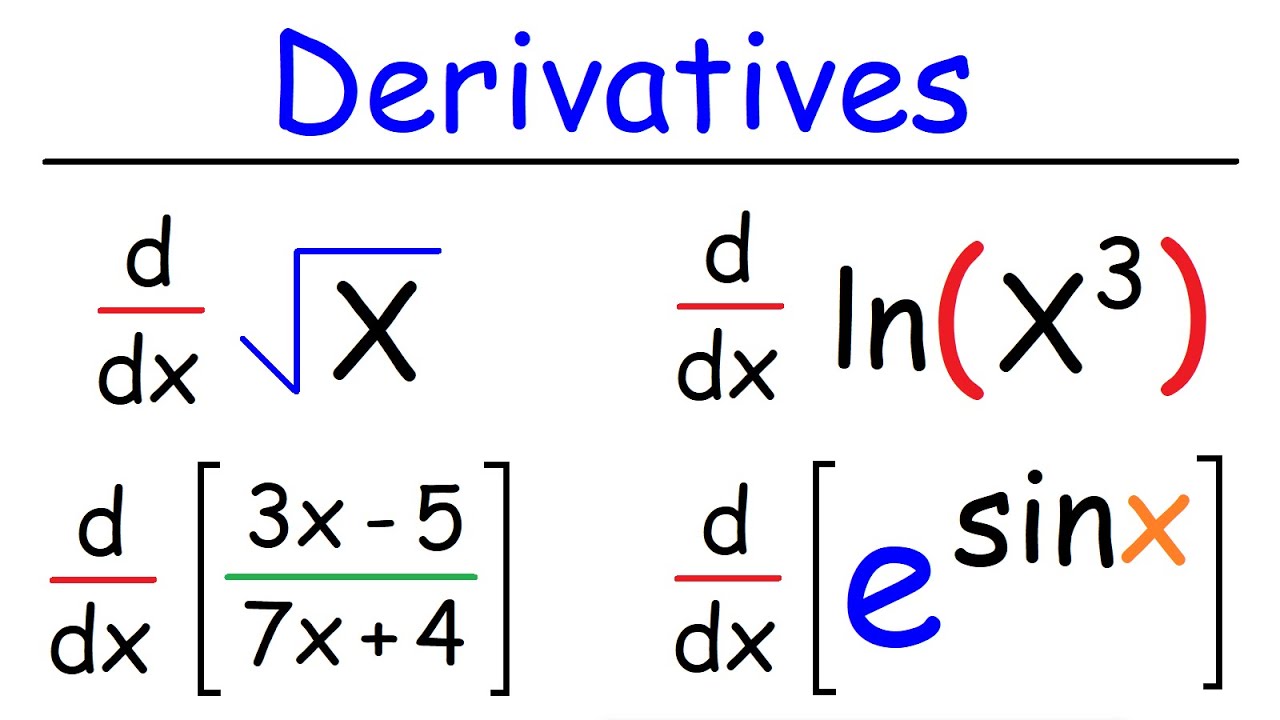
Derivatives for Beginners - Basic Introduction

Basic Derivative Rules - Part 2: Combining the Rules
5.0 / 5 (0 votes)
Thanks for rating: