Calculus 1 Lecture 2.3: The Product and Quotient Rules for Derivatives of Functions
TLDRIn this transcript, the speaker introduces advanced calculus concepts, focusing on the product rule and quotient rule for derivatives. They explain the product rule by demonstrating that derivatives cannot be separated by multiplication and provide a step-by-step example using basic functions. The quotient rule is introduced with an emphasis on its necessity when dealing with complex functions. The speaker also highlights the importance of understanding these rules for future topics like the chain rule. Throughout the explanation, the speaker encourages hands-on practice and verification of the rules, emphasizing their utility in simplifying calculus problems.
Takeaways
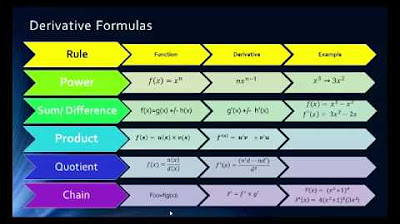
- 📚 The Product Rule states that the derivative of a product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function.
- 🔢 The Quotient Rule is used to find the derivative of a quotient of two functions. It is not as straightforward as separating the derivative into the numerator and the denominator; instead, it involves a specific formula.
- 🚫 You cannot separate derivatives by multiplication or division directly. The Product and Quotient Rules provide the correct method for finding derivatives in these cases.
- 🌟 Understanding the difference between constants and functions is crucial when applying the Product Rule. Constants can be factored out and do not require the rule, while functions must be treated with the rule.
- 📈 The derivative represents the slope of a curve at a specific point. The Product and Quotient Rules help in finding this slope for complex functions.
- 🔍 The process of differentiating complex functions involves breaking them down into simpler parts using the Product and Quotient Rules, making the problem more manageable.
- 📊 When applying the Quotient Rule, it's important to remember the order of operations. The derivative of the numerator and the derivative of the denominator are not interchangeable due to the subtraction involved.
- 🧩 The video script provides an example of how the Product Rule can be used within the Quotient Rule, showing how the rules can be combined to solve more complex problems.
- 🎓 The video emphasizes the importance of practice and understanding of the rules, suggesting that with a solid grasp of the Product and Quotient Rules, calculus becomes a more straightforward subject.
- 📝 The video script encourages reading the book for proofs of the Product and Quotient Rules, reassuring that they are not too difficult to follow and can enhance understanding of the concepts.
Q & A
What is the main topic discussed in the transcript?
-The main topic discussed in the transcript is the concept and application of the product rule and quotient rule in calculus, specifically in finding the derivatives of functions.
What are the two basic functions given as an example in the transcript?
-The two basic functions given as an example are f(x) = x squared and g(x) = x cubed.
What is the product rule used for in calculus?
-The product rule is used for finding the derivative of a product of two functions. It provides a formula to break down the derivative of a product into simpler parts.
How is the product rule expressed mathematically?
-The product rule is expressed mathematically as: (d/dx)[f(x)*g(x)] = f'(x)*g(x) + f(x)*g'(x), where f'(x) and g'(x) represent the derivatives of the functions f(x) and g(x), respectively.
What is the quotient rule mentioned in the transcript, and what does it relate to?
-The quotient rule is a concept in calculus that relates to finding the derivative of a quotient of two functions. It is not fully explained in the transcript but is mentioned as a topic for further discussion.
What is the main difference between the product rule and the quotient rule?
-The main difference is that the product rule is used for finding the derivative of a product of two functions, while the quotient rule is used for finding the derivative of a quotient (one function divided by another).
Why can't we separate derivatives by multiplication according to the transcript?
-We cannot separate derivatives by multiplication because it does not hold true in general. The transcript provides an example where the derivative of a product of two functions does not equal the product of their individual derivatives.
What is the significance of the example x^5 in the transcript?
-The example of x^5 is used to demonstrate that the derivative of the product of f(x) and g(x) does not equal the product of their individual derivatives. It shows that the product rule is necessary for finding the correct derivative in such cases.
What is the role of the product rule in simplifying calculus problems?
-The product rule plays a crucial role in simplifying calculus problems by allowing us to break down complex derivatives into simpler parts. This makes the process of finding derivatives more manageable and less prone to errors.
What is the derivative of x^2 - 1 according to the transcript?
-The derivative of x^2 - 1, as discussed in the transcript, is 2x * (x^3 + 2x - 3x^2 - 2), which simplifies to 2x * (x^3 - x^2 - 2x - 2).
How does the transcript illustrate the application of the product rule in problem-solving?
-The transcript illustrates the application of the product rule through several examples, where it shows how to break down the derivative of a product of functions into simpler components using the rule. This includes setting up the problem, applying the rule, and simplifying the result.
Outlines
📚 Introduction to Derivatives and the Product Rule
This paragraph introduces the concept of derivatives and sets the stage for discussing the product rule. It begins by questioning the validity of separating derivatives by multiplication, using the example of the derivative of a product of two functions. The speaker then explains that while one might assume that the derivative of a product of two functions is the product of their derivatives, this is not always true. The paragraph sets up a scenario with two basic functions, f(x) = x^2 and g(x) = x^3, to explore this concept further. It emphasizes the importance of understanding the correct method for differentiating a product of functions, leading into the discussion of the product rule in the following paragraphs.
📈 Explanation and Application of the Product Rule
In this paragraph, the product rule is introduced and explained. The rule states that the derivative of a product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function. The speaker provides a step-by-step walkthrough of how to apply the product rule using the previously introduced functions f(x) and g(x). The example calculation demonstrates the process of finding the derivative of x^2 times x^3, leading to the correct answer of 5x^4. The paragraph emphasizes the importance of the product rule when dealing with more complex functions and the inefficiency of trying to distribute derivatives in certain situations.
🔢 Verification of the Product Rule and Introduction to the Quotient Rule
This paragraph focuses on verifying the product rule through examples and introducing the concept of the quotient rule. The speaker reinforces the product rule's correctness by showing that distributing derivatives can yield the same result. The paragraph then transitions to discussing the quotient rule, highlighting that it cannot be applied in the same manner as the product rule. The speaker hints at the complexity of the quotient rule and sets the stage for its detailed explanation in the next paragraphs, emphasizing the need for understanding the product rule before delving into the quotient rule.
🌟 Further Examples and Explanation of the Product Rule
The paragraph continues to explore the product rule with additional examples, emphasizing its utility and importance in calculus. The speaker demonstrates how the product rule can be applied to various functions and how it simplifies the process of finding derivatives. The paragraph also addresses common misconceptions about the product rule and clarifies when it should be used. The speaker encourages students to practice the product rule and to seek proof of its validity in their textbooks, setting the foundation for understanding more advanced calculus concepts.
📝 Application of the Product Rule to Specific Functions
This paragraph delves into the application of the product rule to specific functions, providing a detailed example of how to use the rule to find the derivative of a given function. The speaker walks through the process step by step, emphasizing the importance of following the correct order of operations and understanding the underlying mathematical principles. The example given illustrates the product rule's practical application and helps to solidify the concept in the students' minds, preparing them for more complex problems and the introduction of the quotient rule in subsequent paragraphs.
🔄 Interplay of the Product and Quotient Rules
The paragraph discusses the interplay between the product and quotient rules, highlighting how they can be used in conjunction with each other. The speaker provides an example where a function involves both a product and a quotient, necessitating the use of both rules for correct differentiation. The paragraph emphasizes the importance of understanding the order in which to apply these rules and the necessity of the product rule as a foundation for understanding the more complex quotient rule. The speaker also hints at the upcoming discussion of the quotient rule and the challenges it presents.
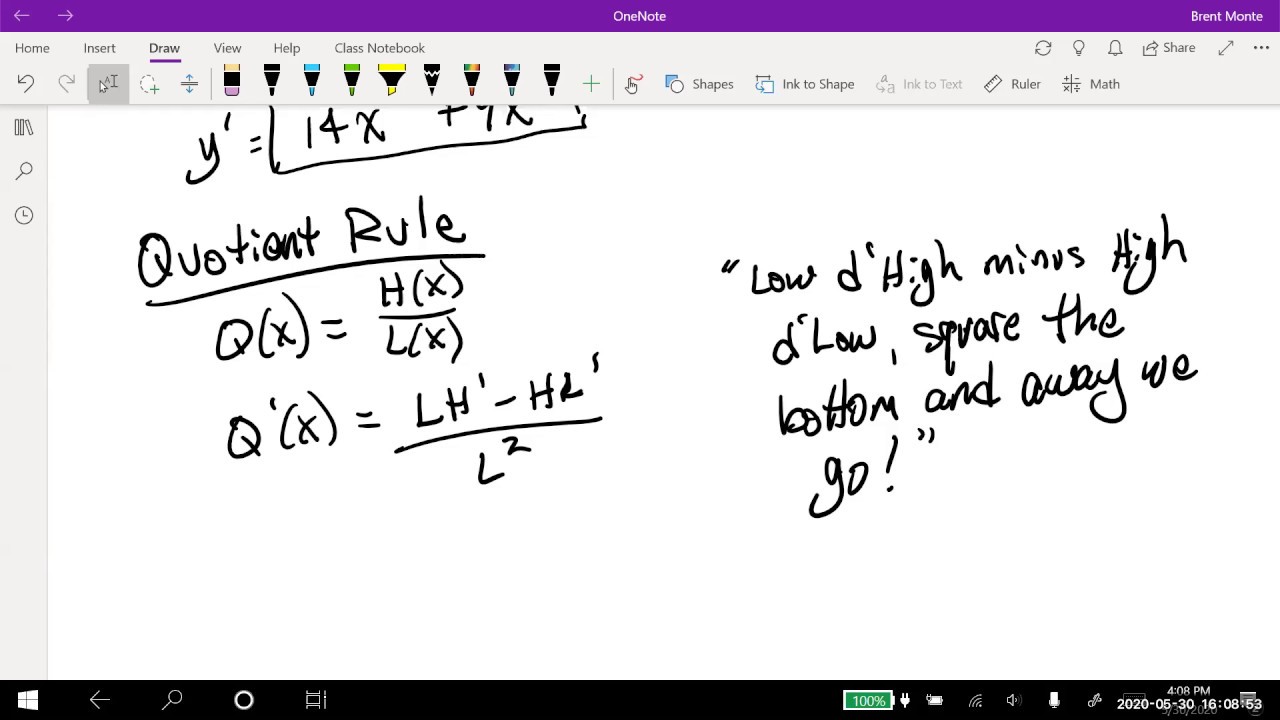
📊 Deriving Quotients and the Quotient Rule
This paragraph focuses on the quotient rule, which is used to find the derivative of a quotient of two functions. The speaker clarifies that the quotient rule cannot be simplified by just taking the derivative of the numerator and dividing by the derivative of the denominator. The quotient rule is introduced with an explanation of its formula, which involves the derivative of the numerator and the derivative of the denominator, with a specific order that must be followed. The speaker provides an example to illustrate the quotient rule's application and emphasizes the importance of memorizing the formula and understanding the rule's order-dependency.
📌 Complex Application of the Quotient Rule
The paragraph presents a complex example that requires the application of the quotient rule. The speaker guides the students through the process of differentiating a function that involves a quotient, emphasizing the need to follow the quotient rule's formula precisely. The example demonstrates the step-by-step process of applying the quotient rule, including distributing the derivative of the numerator and combining like terms. The speaker also highlights the importance of understanding when to use the quotient rule and how it differs from the product rule in terms of application and complexity.
📈 Combining Rules and Solving Challenging Problems
This paragraph discusses the combination of rules, specifically the product and quotient rules, to solve more challenging calculus problems. The speaker provides an example that requires the use of both rules, illustrating how they can be nested within each other. The example shows the process of differentiating a complex function by first applying the quotient rule and then the product rule within the process. The speaker emphasizes the importance of understanding the order in which to apply these rules and the necessity of being able to use one rule within the application of another.
Mindmap
Keywords
💡Derivative
💡Product Rule
💡Quotient Rule
💡Slope
💡x to the power of (n)
💡Distributive Property
💡Constant
💡Differentiation
💡Algebraic Manipulation
💡Polynomial
💡Chain Rule
Highlights
Introduction to advanced calculus concepts, focusing on the product rule and quotient rule for derivatives.
Exploration of whether the derivative of a product of two functions can be separated into the product of their derivatives.
Counterexample provided to demonstrate that derivatives cannot be separated by multiplication.
Introducing the product rule as a method to correctly differentiate the product of two functions.
Explanation of the product rule formula and its application with an example of differentiating x^2 * x^3.
Illustration of the quotient rule and its difference from the product rule.
Proof through example that the quotient rule provides the correct derivative for a function divided by another function.
Demonstration of the quotient rule formula and its application with an example involving (x^2 + 1) / (x + 2).
Clarification on the difference between products and constants in the context of the product rule.
Example of using the product rule to differentiate (1 + x^2) * x^2, highlighting the importance of order in the rule.
Discussion on the practical applications of the product and quotient rules, particularly in more complex scenarios.
Explanation of how the product and quotient rules can be combined to solve more intricate calculus problems.
Use of the quotient rule to find the derivative of a complex fraction, emphasizing the importance of correct order and distribution.
Illustration of how the quotient rule can be applied to find the slope of a curve at a specific point.
Example of nested rules application, showing how to use the product rule within the quotient rule for more complex functions.
Final thoughts on the importance of understanding the interplay between different calculus rules for solving a variety of problems.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: