The Chain Rule... How? When? (NancyPi)

NancyPi
3 Sept 201816:36
EducationalLearning
32 Likes 10 Comments

TLDRThe video script introduces the Chain Rule for calculating derivatives, emphasizing its efficiency in saving time. It explains the Chain Rule, also known as the Outside-Inside Rule, through examples, demonstrating how to apply it to composite functions. The video clarifies when the Chain Rule is necessary and provides strategies for recognizing its application, highlighting its importance in various mathematical contexts, including trigonometric and exponential functions. The script also touches on the official formulas and Leibniz notation for the Chain Rule, and concludes with the reminder to be vigilant about its use in different mathematical scenarios.

Takeaways
  • 📚 The Chain Rule is a method for finding the derivative of a composite function, where a simpler function is inside a larger, outer function.
  • ⏱️ Time efficiency is a key advantage of the Chain Rule, as it simplifies the process of differentiating complex functions.
  • 🔍 You know you need the Chain Rule when there's a smaller 'x' expression or function inside a larger function, and the inner function is not just 'x'.
  • 📝 Also known as the 'Outside-Inside Rule', the Chain Rule involves differentiating the outer function first and then the inner function.
  • 🤓 The Chain Rule can be applied even if the inner derivative is 1, as it's a safer approach and doesn't change the result, but ensures accuracy.
  • 🌟 The Chain Rule is not limited to two functions; it can be extended to multiple nested functions, forming a 'chain' of derivatives.
  • 📊 Examples of functions where the Chain Rule is necessary include (3x + 1)^7, (x + 1)^7, and (x^2 + 1)^7, as they are composite functions.
  • 🛠️ The Chain Rule can be used in conjunction with other rules like the Product Rule, Quotient Rule, and even itself multiple times for deeply nested functions.
  • 📈 The derivative of a function like sin(x^2) requires the Chain Rule, as the x^2 is the inner function with respect to the outer sine function.
  • 🎓 Understanding the Chain Rule is crucial for mastering calculus, as it's a fundamental concept for differentiating composite functions.
Q & A

  • What is the Chain Rule in calculus?

    -The Chain Rule is a method used to find the derivative of a composite function, which is a function composed of one function inside a larger, outer function. It simplifies the process of differentiation by breaking it down into smaller, more manageable steps.

  • Why is the Chain Rule important to learn?

    -The Chain Rule is important because it saves time and effort when finding derivatives of complex functions. It allows you to break down the process into simpler steps, making it more efficient and less prone to errors.

  • What is another name for the Chain Rule?

    -The Chain Rule is also known as the Outside-Inside Rule, which indicates the order in which you should apply the derivatives: first the outer function, then the inner function.

  • How do you know when to apply the Chain Rule?

    -You should apply the Chain Rule when you have a composite function, meaning a smaller function (x expression) is nested inside a larger function. If the inner function is something other than just x, the Chain Rule is necessary.

  • What is the Power Rule in calculus, and how is it used in the Chain Rule?

    -The Power Rule states that the derivative of a function in the form of x^n, where n is a constant, is n*x^(n-1). In the Chain Rule, the Power Rule is used to find the derivative of the outer function when it involves powers, and it helps in simplifying the expression before multiplying by the derivative of the inner function.

  • Can you give an example of a situation where the Chain Rule is not needed?

    -The Chain Rule is not needed when dealing with simple functions that do not involve composite functions, such as x^7 or 3x + 1, where there is no inner function nested within an outer function.

  • What is the Leibniz notation for the Chain Rule, and when might it be used?

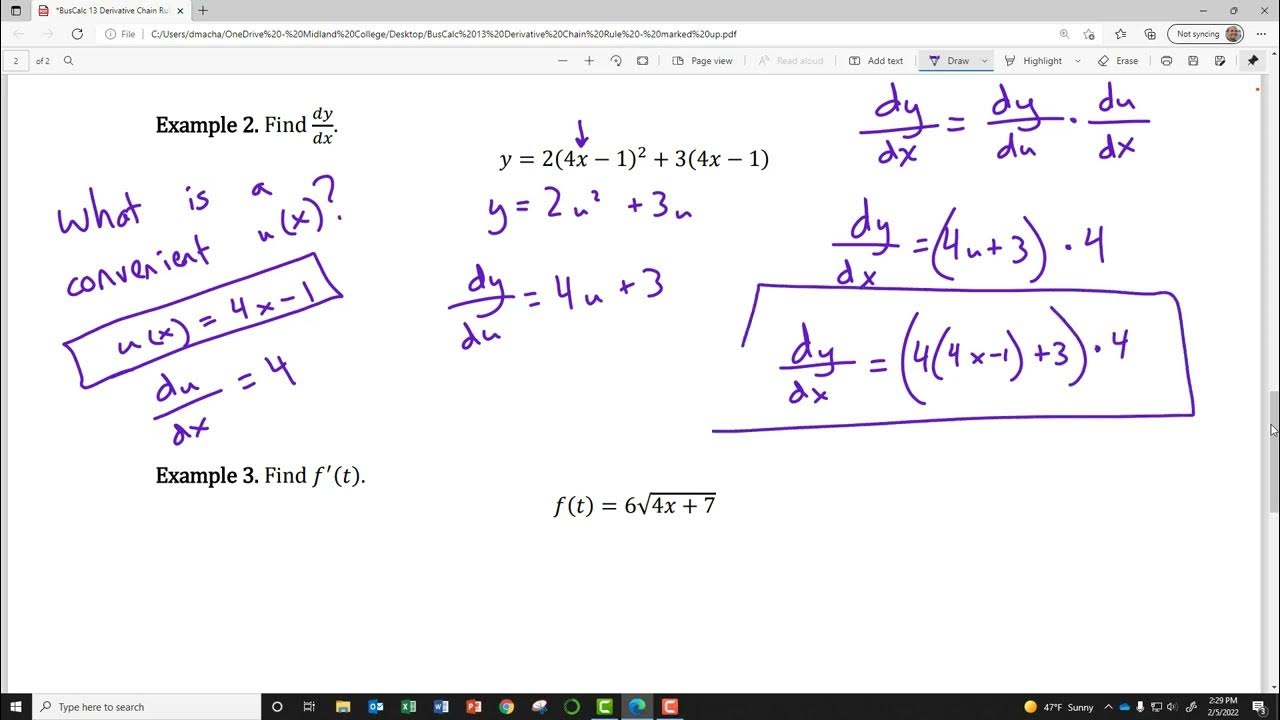
    -The Leibniz notation for the Chain Rule is expressed as dy/du * du/dx, where dy/du represents the outside derivative and du/dx represents the inside derivative. This notation might be used in more advanced calculus topics or when working in different variable contexts.

  • How does the Chain Rule apply to trigonometric functions?

    -The Chain Rule applies to trigonometric functions in the same way as other functions. For example, if you have a function like sin(x^2 - 3x), you would first take the derivative of the outer function (sin), which is cos, and then multiply by the derivative of the inner function (2x - 3).

  • What happens when you need to use the Chain Rule more than once?

    -In cases where you have multiple layers of nested functions, you may need to apply the Chain Rule multiple times to fully differentiate the composite function. Each time, you would find the derivative of the immediate outer function and then multiply by the derivative of the next inner function.

  • Can you identify a few forms of functions that would require the Chain Rule?

    -Functions that require the Chain Rule include those with nested smaller x expressions within larger function forms, such as e^(3x) with 3x inside the exponential, ln(5x) with 5x inside the natural log, or (x^2 + 1)^(1/2) with x^2 + 1 under the square root.

  • What is the significance of the Chain Rule in more complex calculus problems?

    -The Chain Rule is significant in more complex calculus problems as it allows for the differentiation of composite functions, which are common in advanced topics. It helps in breaking down complex expressions into simpler parts, making the differentiation process more manageable and less error-prone.

Outlines
00:00
📚 Introduction to the Chain Rule

This paragraph introduces the Chain Rule as a crucial concept in calculus for finding derivatives. Nancy explains the importance of understanding the Chain Rule, emphasizing that it saves time and simplifies the process of differentiating composite functions. The Chain Rule is applicable when there is a smaller x expression or function inside a larger, outer function. The paragraph outlines the basic procedure of the Chain Rule, also known as the Outside-Inside Rule, which involves taking the derivative of the outer function first and then multiplying by the derivative of the inner function. An example is provided to illustrate the process, showing how to apply the Power Rule and the Constant Multiple Rule within the Chain Rule.

05:02
🤔 When to Apply the Chain Rule

This section delves into the conditions under which the Chain Rule is necessary. It clarifies that the Chain Rule is not needed for simple functions like x^7, but it is essential for composite functions such as (3x + 1)^7. The paragraph presents a series of examples and questions to help viewers determine when the Chain Rule is required. It also touches on the potential pitfalls of not using the Chain Rule when it is needed, emphasizing that it's better to use the Chain Rule as a precaution even when the inner derivative might seem to have no impact.

10:03
🔄 Advanced Chain Rule Applications

This paragraph explores more complex applications of the Chain Rule, including cases where it is necessary to apply the Chain Rule multiple times. The explanation includes a variety of functions, such as those involving trigonometric functions, exponentials, and nested functions. The paragraph also introduces the official formula for the Chain Rule and explains its significance in more intricate scenarios. The concept of nested functions and the need for multiple applications of the Chain Rule are highlighted, emphasizing the importance of considering every level of differentiation to arrive at the correct overall derivative.

15:07
📈 Diverse Forms of the Chain Rule

The final paragraph discusses the diverse forms in which the Chain Rule might be applied, such as within the Quotient Rule, Product Rule, or in combination with other mathematical concepts like exponentials and logarithms. It provides examples of scenarios where the Chain Rule is essential, including functions with exponentials, logarithms, square roots, and fractional powers. The paragraph serves as a reminder to be vigilant about identifying when the Chain Rule is needed, even in less obvious cases. The video concludes with an encouragement for viewers to engage with the content and a call to action for likes and subscriptions.

Mindmap
Keywords
💡Chain Rule
The Chain Rule is a fundamental concept in calculus for finding the derivative of a composite function, which is a function made up of one function nested inside another. It is used when there is a smaller 'inner' function within a larger 'outer' function. The rule states that to find the derivative of the composite function, you take the derivative of the outer function and multiply it by the derivative of the inner function. In the video, the Chain Rule is illustrated with examples such as (3x + 1)^7 and (x^2 + 1)^7, emphasizing its importance in simplifying the process of differentiation and saving time.
💡Derivative
A derivative is a concept in calculus that represents the rate of change or the slope of a function at a particular point. It is a fundamental tool for analyzing the behavior of functions, especially in terms of their increases and decreases, maxima, and minima. In the context of the video, the derivative is calculated using the Chain Rule for various composite functions, such as the power function, trigonometric functions, and exponential functions.
💡Power Rule
The Power Rule is a basic differentiation rule in calculus that states if you have a function of the form f(x) = x^n, where n is a constant, the derivative of the function is f'(x) = n * x^(n-1). This rule is used when taking the derivative of a power function, which is one of the simplest types of functions in calculus. In the video, the Power Rule is applied to the outer function when using the Chain Rule, such as taking the derivative of (7*(3x + 1)^6).
💡Composite Function
A composite function is a function that is made up of two or more functions combined together, where the output of one function becomes the input of another. This is a crucial concept in the Chain Rule, as it is the scenario where the Chain Rule is most commonly applied. In the video, several examples of composite functions are given, such as sin(x^2) and e^(3x), to demonstrate how the Chain Rule is used to find their derivatives.
💡Outside-Inside Rule
The Outside-Inside Rule is an alternative name for the Chain Rule in calculus. It provides a clear mnemonic for how to apply the Chain Rule: first, take the derivative of the 'outside' or outer function, and then multiply that by the derivative of the 'inside' or inner function. This rule is emphasized in the video as a way to remember the steps involved in differentiating composite functions using the Chain Rule.
💡Constant Multiple Rule
The Constant Multiple Rule is a basic differentiation rule stating that if a function is a constant multiplied by a variable, such as 3x, the derivative is simply the constant, which in this case is 3. This rule is used when differentiating terms in a function that are constants or have a constant coefficient. In the video, this rule is applied when finding the derivative of the inner function in the example (3x + 1)^7.
💡Trigonometric Functions
Trigonometric functions, such as sine (sin) and cosine (cos), are mathematical functions that relate angles to real numbers. They are widely used in various fields, including physics and engineering, to model periodic phenomena. In the video, the Chain Rule is applied to trigonometric functions, such as sin(x^2) and sin(3x), to demonstrate how to differentiate these functions when they are part of composite functions.
💡Exponential Functions
Exponential functions are mathematical functions of the form f(x) = a^x, where 'a' is a constant and 'x' is the variable. These functions grow rapidly as 'x' increases and are used to model a variety of real-world phenomena, such as population growth and radioactive decay. In the video, the Chain Rule is used to differentiate exponential functions like e^(3x) and demonstrates the importance of the Chain Rule in handling complex exponential expressions.
💡Differentiation
Differentiation is the process of finding the derivative of a function, which gives the rate of change or the slope of the function at any point. It is a core operation in calculus and is essential for understanding the behavior of functions. The video focuses on teaching the Chain Rule as a method of differentiation, showing how it simplifies the process of finding derivatives for composite functions.
💡Leibniz Notation
Leibniz Notation is a historical method of expressing derivatives, named after the mathematician and philosopher Gottfried Wilhelm Leibniz. It uses a 'd' symbol followed by the variable of differentiation and a 'dx' to denote the derivative with respect to 'x'. In the video, the Leibniz Notation is briefly mentioned as an alternative way to represent derivatives, with the 'dy/du' representing the outer derivative and 'du/dx' representing the inner derivative in the context of the Chain Rule.
💡Rate of Change
The rate of change is a fundamental concept in calculus that describes how a quantity changes in response to changes in another quantity. It is the essence of what a derivative represents, quantifying the instantaneous change or slope of a function at a specific point. In the video, the Chain Rule is presented as a tool for efficiently calculating the rate of change for complex functions, emphasizing its practicality in saving time and effort when differentiating composite functions.
Highlights

Introduction to the Chain Rule for finding derivatives.

The Chain Rule saves time in calculus.

The Chain Rule applies to complicated equations with a function inside a larger, outer function.

The alternative name for Chain Rule is the 'Outside-Inside Rule'.

To apply the Chain Rule, take the derivative of the outer function first and leave the inside part untouched.

Use the Power Rule to find the derivative of a power function.

The Chain Rule involves multiplying by the derivative of the inner function after taking the derivative of the outer function.

The Chain Rule is necessary when there is a smaller x expression or function inside a larger function.

Examples are provided to illustrate the application of the Chain Rule.

The Chain Rule is not needed for simple functions like x^7 or 3x + 1 without an inner function.

The Chain Rule should be used even when the inner derivative might be 1, as it's a safe practice.

Explanation of when not to use the Chain Rule, such as with simple powers or polynomials without composite functions.

Demonstration of how the Chain Rule simplifies the process of taking derivatives compared to expanding and distributing terms.

Presentation of a more complicated example involving a power of a trinomial and the use of the Chain Rule.

Lightning round game to identify when the Chain Rule is needed.

Explanation of the official formulas for the Chain Rule in both standard and Leibniz notation.

Discussion on the necessity of including the inner derivative in the overall derivative calculation.

Examples of trigonometric functions where the Chain Rule is applied.

Explanation of situations where the Chain Rule may need to be applied multiple times for nested functions.

Additional examples of functions where the Chain Rule is necessary, such as exponentials and logarithms.

Encouragement to like and subscribe to the video for more content on the Chain Rule and calculus.

Transcripts

Browse More Related Video

Business Calculus - Math 1329 - Section 2.4 - Chain Rule

Calculus AB Lesson 3.4 The Chain Rule

BusCalc 13 Derivative Chain Rule

Chain Rule Day 1

The Chain Rule - Part 1

Calculus 1 Lecture 2.6: Discussion of the Chain Rule for Derivatives of Functions

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
DerivativeCalculusMathematicsTutorialChainRuleExplanationEfficiencyInMathInsideOutsideRulePowerRuleApplicationCompositeFunctionsTrigonometricDerivativesExponentialLogarithmicCalculusFundamentalsEducationalContent