The Chain Rule - Part 1
TLDRThe video script introduces the concept of the chain rule, a fundamental principle in calculus for finding the derivative of a composite function. It explains that a composite function consists of an 'inside' and an 'outside' function, and the chain rule allows one to find the derivative by multiplying the derivative of the outside function with the derivative of the inside function. The script walks through several examples, illustrating how to apply the chain rule to different types of functions, including polynomials, exponentials, and radicals. It emphasizes the importance of recognizing the structure of composite functions and applying the chain rule in a step-by-step manner. The summary aims to provide a clear understanding of the chain rule, making it accessible to those studying calculus.
Takeaways
- 📌 **Composite Function Identification**: Recognize a composite function as a function within another function, such as "y = f(g(x))".
- 🔍 **Inside and Outside Functions**: Differentiate between the inside function ("g(x)") and the outside function ("f(x)") in a composite function.
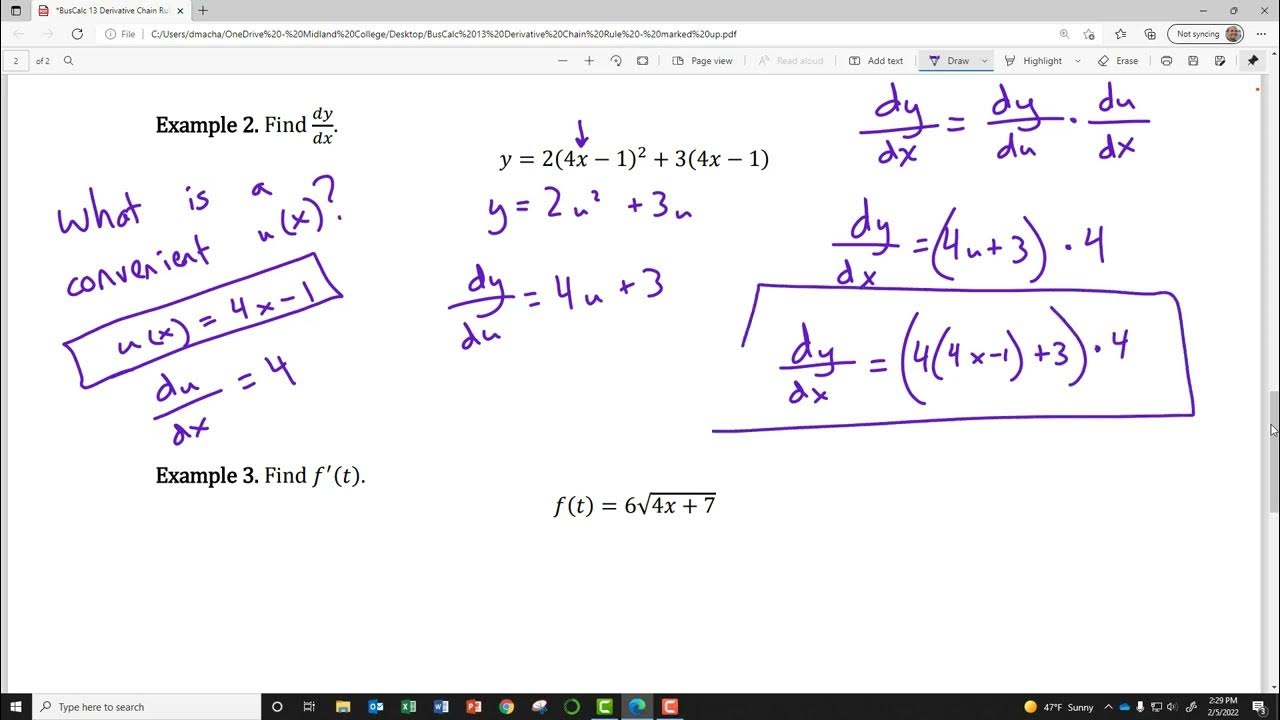
- 📈 **Chain Rule Application**: Use the chain rule to find the derivative of a composite function, which is expressed as "(f(g(x)))' = f'(g(x)) · g'(x)".
- 📝 **Power Rule Integration**: When dealing with a composite function involving exponents, apply the power rule by bringing down the exponent and then differentiating the inside function.
- 🔗 **Chain Linking**: Remember that the chain rule involves multiplying the derivatives of the inside and outside functions together, creating a 'chain' of operations.
- ✅ **Exponential Function Derivatives**: For exponential functions, the derivative of "e^{g(x)}" is "e^{g(x)} · g'(x)", using the general rule for derivatives of exponential functions.
- 🛠️ **Derivative of Radicals**: When differentiating a radical, rewrite the expression as a power and apply the power rule, then use the chain rule to include the derivative of the inside function.
- 🔑 **Quotient Rule Variation**: For quotients, rewrite the expression to make use of the chain rule, by setting "u = g(x)" and transforming the quotient into "1/u" raised to an appropriate power.
- 🧹 **Simplifying the Derivative**: After applying the chain rule, simplify the derivative by combining like terms and rewriting expressions for clarity.
- 📐 **Derivative of Polynomials**: When the inside function of a composite function is a polynomial, apply the power rule to the polynomial's terms and then multiply by the derivative of the polynomial using the chain rule.
- 📘 **General Chain Rule Formula**: For a function "y = f(g(x))", the derivative can be found using "f'(u) · u'", where "u = g(x)", as a shortcut method for finding the derivative.
Q & A
What is a composite function?
-A composite function is a function that consists of one function nested inside another function. It is represented as y = f(g(x)), where g(x) is the inside function and f(x) is the outside function.
How do you identify the inside and outside functions in a composite function?
-To identify the inside and outside functions, look for the function that is nested within another. The inside function is the one that is enclosed within the parentheses of the outer function, and the outside function is the one that contains the inside function.
What is the chain rule in calculus?
-The chain rule is a fundamental theorem for differentiation that is used to find the derivative of a composite function. It states that the derivative of y = f(g(x)) is given by dy/dx = f'(g(x)) * g'(x), where f'(u) is the derivative of the outer function with respect to u, and g'(x) is the derivative of the inner function with respect to x.
How is the power rule applied when using the chain rule?
-When using the chain rule, the power rule is applied by taking the exponent of the inside function and bringing it down in front of the function itself. Then, the power of the inside function is reduced by one. For example, if the inside function is (3x + 2)^2, the power rule would apply by bringing down the exponent 2 to get 2(3x + 2)^1.
What is the derivative of an exponential function with respect to x?
-The derivative of an exponential function y = e^x with respect to x is simply e^x. This is because the exponential function e^x is its own derivative.
How do you apply the chain rule to a function with a radical?
-To apply the chain rule to a function with a radical, rewrite the radical as a power, such as the square root as x^(1/2). Then apply the power rule by bringing down the exponent and adjusting the power accordingly. Finally, multiply by the derivative of the inside function.
What is the derivative of y = (x^2 + 2x)^(-1) with respect to x?
-The derivative of y = (x^2 + 2x)^(-1) with respect to x is found by first applying the power rule to bring down the exponent -1, resulting in -1(x^2 + 2x)^(-2), and then multiplying by the derivative of the inside function, which is 2x + 2, to get -1(2x + 2)/(x^2 + 2x)^2.
How do you differentiate a quotient of two functions?
-To differentiate a quotient of two functions, let u be the numerator and v be the denominator. Then, use the quotient rule, which states that the derivative of u/v is (v * u' - u * v') / v^2, where u' and v' are the derivatives of u and v, respectively.
What is the general rule for finding the derivative of a function in the form y = f(ax + b)?
-The general rule for finding the derivative of a function in the form y = f(ax + b) is to apply the chain rule. It involves differentiating the outer function f with respect to its argument (ax + b) and then multiplying by the derivative of the argument, which is a.
Why is it important to recognize a composite function when finding derivatives?
-Recognizing a composite function is important because it indicates the need to use the chain rule for differentiation. The chain rule allows you to break down the differentiation process into steps, applying the derivative of the outer function to the result of the inner function's derivative.
How does the chain rule relate to the concept of a 'chain'?
-The chain rule relates to the concept of a 'chain' because it involves a sequence of steps or 'links' where the derivative of the outer function is multiplied by the derivative of the inner function. Each step in the differentiation process is connected or 'chained' to the next, hence the name.
Outlines
📚 Introduction to the Chain Rule
This paragraph introduces the concept of the chain rule, which is essential for finding the derivative of a composite function. A composite function is defined as a function within another function, and the paragraph explains how to identify and break down such functions into 'inside' and 'outside' functions. The formula for the chain rule is presented as f'(u) * u', where f is the outside function and u is the inside function. The paragraph also includes an example of finding the derivative of y = (3x + 2)^2, demonstrating the application of the chain rule and the power rule.
🔗 Applying the Chain Rule to Composite Functions
The second paragraph delves deeper into applying the chain rule to various types of composite functions. It covers examples including a function with an exponential as the outside function, a radical function, and a quotient function. The paragraph emphasizes the importance of differentiating the inside function and then multiplying the results according to the chain rule. Each example illustrates the step-by-step process of applying the chain rule, including simplifying the expressions to obtain the final derivatives.
🧮 Advanced Chain Rule Applications
The final paragraph discusses more complex applications of the chain rule, particularly with quotients and functions raised to fractional powers. It shows how to rewrite the given function to make the chain rule application more straightforward. The paragraph explains the process of applying both the chain rule and the power rule to find derivatives, including simplifying expressions and rearranging terms for clarity. The examples provided demonstrate the methodical approach to differentiating composite functions using the chain rule, even when the functions are more complicated.
Mindmap
Keywords
💡Chain Rule
💡Composite Function
💡Derivative
💡Power Rule
💡Exponential Function
💡Inside Function
💡Outside Function
💡Square Root
💡Quotient
💡Differentiation
💡Exponent
Highlights
Introduction to the chain rule for finding derivatives of composite functions.
Defining a composite function as a function within another function.
Identifying the inside function (g(x)) and outside function (f(x)) in a composite function y = f(g(x)).
Breaking down composite functions into outside and inside functions with examples.
Using the power rule to find derivatives when a quantity is raised to a power within a composite function.
Applying the chain rule formula f'(u) * u' where u is the inside function.
Demonstrating the chain rule with an example of y = (3x + 2)^2.
Deriving the outside function first, then multiplying by the derivative of the inside function.
Applying the chain rule to an exponential function, y = e^(3x^2 + 2).
Using the general rule for the derivative of an exponential function and then applying the chain rule.
Deriving a function with a radical, y = √(x^2 + 3), by rewriting it with a power and applying the chain rule.
Rewriting a quotient function as a reciprocal and applying both the chain rule and power rule.
Simplifying expressions by combining like terms and using properties of exponents after applying the chain rule.
Handling a composite function with a quotient by letting u = the inside function and rewriting the function.
Applying the chain rule to a more complex composite function, y = (5x^2 - 3x + 2)^(3/2).
Multiplying the derivatives and powers together to simplify the final expression after applying the chain rule.
The importance of recognizing when a function is a composite function for derivative calculations.
The process of differentiating composite functions step by step with clear examples.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: