Physics: Alternative Ways to Think of Sine and Cosine

Smoleny1

15 Sept 201307:54

EducationalLearning

32 Likes 10 Comments

TLDRIn this video, the presenter introduces alternative ways to conceptualize cosine and sine beyond the traditional SOHCAHTOA approach. The focus is on applying these concepts to physics, particularly in dealing with vectors. The presenter suggests thinking of cosine in terms of 'along' the x-axis or another reference axis, and sine in terms of 'across' or perpendicular to that axis. This new perspective is especially useful when working with three-dimensional vectors and complex applications such as dot and cross products, where the traditional definitions may not be as intuitive.

Takeaways

📚 Basic trigonometry teaches us SOHCAHTOA, which relates sine, cosine, and tangent to the sides of a right triangle.
🚫 In physics applications, relying solely on SOHCAHTOA is considered inefficient and akin to using training wheels.
🌐 An alternative way to think of cosine is to associate it with the value along the x-axis or 'X'.
🔄 For the y-component, think of sine as the value across or perpendicular to the x-axis.
📈 When dealing with vectors, the x-component is found using R cosine theta and the y-component using R sine theta.
🔢 In advanced applications like dot products and cross products, traditional SOHCAHTOA may not be applicable.
📊 For vectors not aligned with the x and y axes, think of cosine as the component along the axis ('along') and sine as the component across ('cross').
🤔 Understanding the 'along' and 'cross' concept helps visualize and calculate vector components in 3D space.
🛠️ When calculating work along a vector, use the cosine of the angle; for torque, consider the sine of the angle.
🎓 This alternative perspective on cosine and sine provides a more intuitive approach to vector analysis.
👋 The video aims to enhance the viewer's understanding of these concepts for better application in physics and engineering.

Q & A

What is the traditional way of understanding sine and cosine?
-Traditionally, sine and cosine are understood through the ratios of sides in a right triangle, where sine is the ratio of the length of the side opposite the angle to the length of the hypotenuse, and cosine is the ratio of the length of the adjacent side to the hypotenuse.
Why is using SOHCAHTOA considered tedious in physics applications?
-Using SOHCAHTOA is considered tedious in physics applications because it is a longer and more complicated method, especially when dealing with vector components and advanced concepts like dot products, cross products, and electromagnetic fields.
What is the alternative way to think of cosine in relation to the x-axis?
-The alternative way to think of cosine is to associate it with the value 'X' and to consider it as the component of a vector that lies along the x-axis or in the direction of the reference angle to the x-axis.
How does the concept of sine change when dealing with vector components?
-When dealing with vector components, sine is associated with the 'Y' component of a vector, which is perpendicular to the x-axis or across the reference angle to the x-axis.
What are the limitations of using x and y components when vectors are not aligned with the coordinate axes?
-The limitations include the inability to easily define x and y components when vectors are not aligned with the coordinate axes, as they may be involved in three-dimensional space or have angles that are not easily represented in a 2D plane.
What alternative terminology is suggested for understanding cosine in vector operations?
-An alternative terminology for understanding cosine in vector operations is to think of it as 'along', meaning the component of a vector that lies along the axis or direction of another vector.
How is sine described in the context of vector components and angles?
-In the context of vector components and angles, sine is described as 'across', referring to the component of a vector that is perpendicular or crossed with the axis or direction of another vector.
How does the concept of 'along' and 'across' help in visualizing vector components?
-The concepts of 'along' and 'across' help in visualizing vector components by providing a clearer understanding of the direction and orientation of the components relative to other vectors or axes, which is crucial for operations like dot products and cross products.
What is the significance of understanding the 'along' and 'across' components in physics applications?
-Understanding the 'along' and 'across' components is significant in physics applications as it allows for a better grasp of the directionality and magnitude of forces, work, torque, and other vector quantities, which is essential for accurate calculations and problem-solving in physics.
How can the concepts of cosine and sine be applied to find the angle between two vectors?
-The concepts of cosine and sine can be applied to find the angle between two vectors by considering the dot product and cross product of the vectors. The cosine of the angle is related to the dot product, while the sine of the angle is related to the cross product magnitude.
What is the main takeaway from the video regarding the use of cosine and sine in physics?
-The main takeaway is that while traditional methods like SOHCAHTOA are foundational, using the concepts of 'along' for cosine and 'across' for sine provides a more intuitive and practical approach for dealing with vector components and advanced physics applications.

Outlines

00:00

📚 Introduction to Alternative Concepts of Cosine and Sine

The video begins with an introduction to alternative ways of understanding cosine and sine, moving beyond the traditional definitions of sohcahtoa. The speaker emphasizes the limitations of these basic definitions, especially in the context of physics applications, and suggests that relying on them is akin to using training wheels. The goal is to explore more advanced and practical ways of thinking about these trigonometric functions.

05:01

🌟 Relating Cosine and Sine to Vector Components

The speaker introduces a new way of associating cosine and sine with vector components. When dealing with vectors, the cosine is related to the component of the vector along the x-axis (or the reference axis), and sine is related to the y-component. This approach simplifies the process of breaking down vectors into their constituent parts. However, the speaker also addresses situations where the traditional x and y-axis may not be clearly defined, such as in three-dimensional space or when dealing with complex vector interactions. In these cases, the speaker suggests thinking of cosine in terms of 'along' the axis or vector, and sine in terms of 'across' it, providing a more intuitive understanding for advanced applications.

Mindmap

Keywords

💡cosine

In the context of the video, cosine refers to a mathematical function related to the ratio of the adjacent side to the hypotenuse in a right-angled triangle, and more broadly, to the x-component of a vector when dealing with vector decomposition or transformation. The video emphasizes thinking of 'cosine' as 'along' when considering the vector's orientation with respect to an axis or reference direction, particularly when calculating components along the x-axis or other reference directions in physics applications.

💡sine

Sine is another trigonometric function, analogous to cosine, but it represents the ratio of the opposite side to the hypotenuse in a right-angled triangle. In the video, sine is associated with the y-component of a vector and is suggested to be thought of as 'across' when considering vector orientation. This concept is crucial for understanding vector decomposition and transformation, especially in three-dimensional space where the axes may not be clearly defined.

💡SOHCAHTOA

SOHCAHTOA is a mnemonic acronym used to remember the trigonometric functions sine, cosine, and tangent in relation to the sides of a right-angled triangle. The video suggests that while this method is foundational, it can be seen as tedious and basic when applied to more advanced physics concepts, such as vector operations.

💡vector

A vector is a mathematical object that has both magnitude and direction. In the context of the video, vectors are used to represent physical quantities that have both size and direction, such as force or velocity. The speaker discusses the decomposition of vectors into components along and across axes, which is essential for understanding various physics problems, including dot products, cross products, and flux.

💡dot product

The dot product is a binary operation that takes two vectors and returns a scalar value. It is calculated by multiplying the magnitudes of the vectors and the cosine of the angle between them. In the video, the dot product is mentioned as an application where understanding the components of vectors along and across each other is crucial for calculating the angle and the magnitude of the resultant vector.

💡cross product

The cross product is another binary operation on vectors that results in a new vector, which is perpendicular to both input vectors. It is used to calculate quantities like torque and the area of parallelograms spanned by the vectors. In the video, the cross product is mentioned in the context of dealing with three-dimensional vectors and the need to understand the 'across' or sine component of vectors.

💡reference angle

A reference angle is the angle between a line and a reference direction, typically the positive x-axis in the coordinate system. In trigonometry, the reference angle is used to find the values of trigonometric functions for any angle by reducing the angle to a value between 0 and π (or 180 degrees). The video uses the concept of the reference angle to discuss how cosine and sine relate to the components of a vector with respect to the x-axis.

💡angle

An angle in mathematics is a figure formed by two rays, called the sides of the angle, sharing a common endpoint, called the vertex. In the context of the video, angles are crucial for understanding the orientation of vectors and for performing operations such as dot products and cross products. The speaker discusses finding the angle between vectors and how this relates to the components of the vectors.

💡components

In the context of the video, components refer to the individual parts of a vector when it is decomposed into its orthogonal (perpendicular) parts along different axes or reference directions. The decomposition of a vector into components is essential for solving problems in physics and engineering where the effects of forces or motions in different directions need to be considered.

💡physics applications

Physics applications refer to the practical use of physical principles and mathematical methods to solve real-world problems involving forces, motions, energies, and other physical quantities. In the video, the speaker discusses how the concepts of cosine and sine, when applied to vector components, are crucial for solving advanced physics problems, such as calculating work, torque, and electromagnetic flux.

Highlights

The video introduces alternative ways to think about cosine and sine beyond the traditional SOHCAHOOTA approach.

In physics applications, using SOHCAHOOTA is considered tedious and for beginners, hence the need for alternative concepts.

The presenter suggests thinking of cosine in relation to the x-axis and the value X when dealing with reference angles.

For finding x and y components of a vector, the formula R cosine theta is used for the x-component and sine of theta for the y-component.

In more advanced applications like dot and cross products, the traditional SOHCAHOOTA method may not be practical.

When dealing with vectors that do not align with the x and y axes, the presenter advises thinking of cosine as 'along' and sine as 'across'.

The concept of 'along' refers to the component of a vector that lies parallel to another vector or axis.

The 'across' component is perpendicular to the other vector or axis, forming a 90-degree angle.

In three-dimensional space, understanding the 'along' and 'across' components helps in visualizing and calculating dot and cross products.

The magnitude times the cosine corresponds to the 'along' component, while the magnitude times the sine corresponds to the 'across' component.

This new perspective on cosine and sine is particularly useful for quickly dealing with work and torque calculations.

The video aims to provide a better understanding and visualization of vector operations in physics applications.

The presenter uses humor to engage the audience and make the learning process more enjoyable.

The video concludes by emphasizing the practical value of understanding 'along' and 'across' for dealing with complex vector problems.

Transcripts

Browse More Related Video

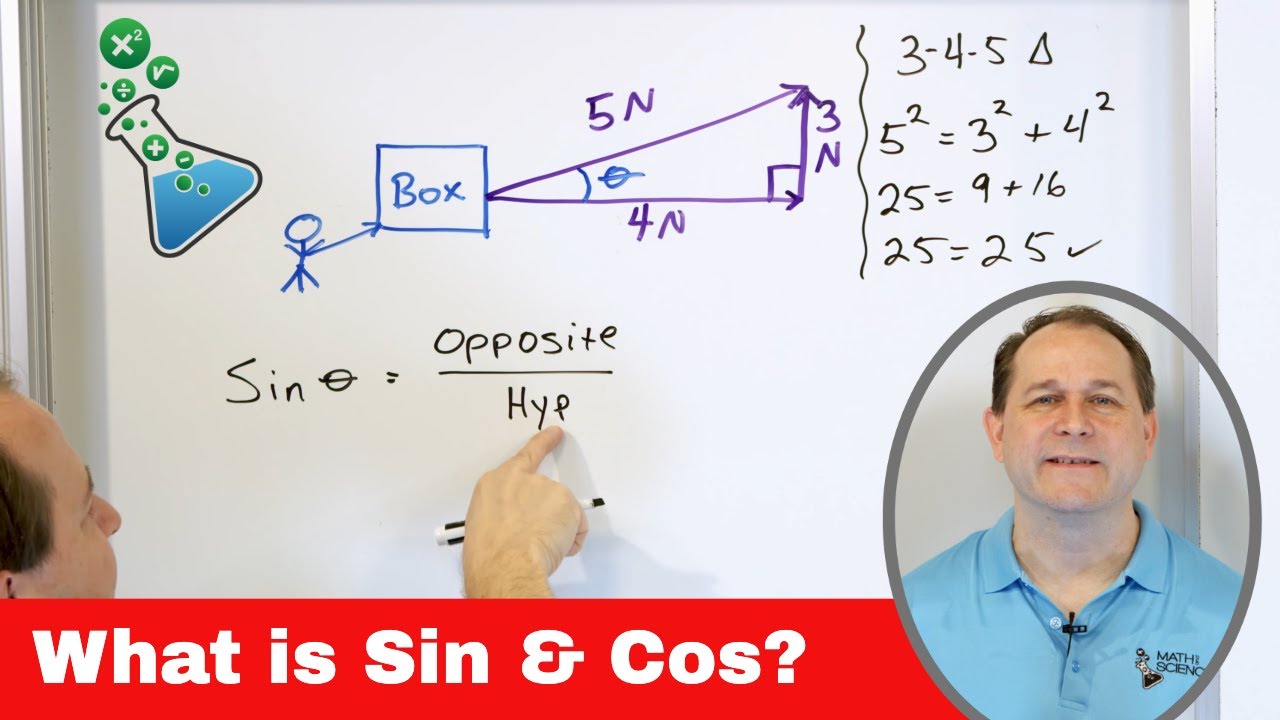
05 - Sine and Cosine - Definition & Meaning - Part 1 - What is Sin(x) & Cos(x) ?

Unit Circle Definition of Trig Functions

Calculus 1 Lecture 5.2: Volume of Solids By Disks and Washers Method

How Do You Know When to Use Cos or Sin in Physics? : Physics & Math

U-Substitution 5-sample video

why there is no four dimensional cross product.

Physics: Alternative Ways to Think of Sine and Cosine

Takeaways

Q & A

What is the traditional way of understanding sine and cosine?

Why is using SOHCAHTOA considered tedious in physics applications?

What is the alternative way to think of cosine in relation to the x-axis?

How does the concept of sine change when dealing with vector components?

What are the limitations of using x and y components when vectors are not aligned with the coordinate axes?

What alternative terminology is suggested for understanding cosine in vector operations?

How is sine described in the context of vector components and angles?

How does the concept of 'along' and 'across' help in visualizing vector components?

What is the significance of understanding the 'along' and 'across' components in physics applications?

How can the concepts of cosine and sine be applied to find the angle between two vectors?

What is the main takeaway from the video regarding the use of cosine and sine in physics?