Calculus Chapter 4 Lecture 30 Simple Areas

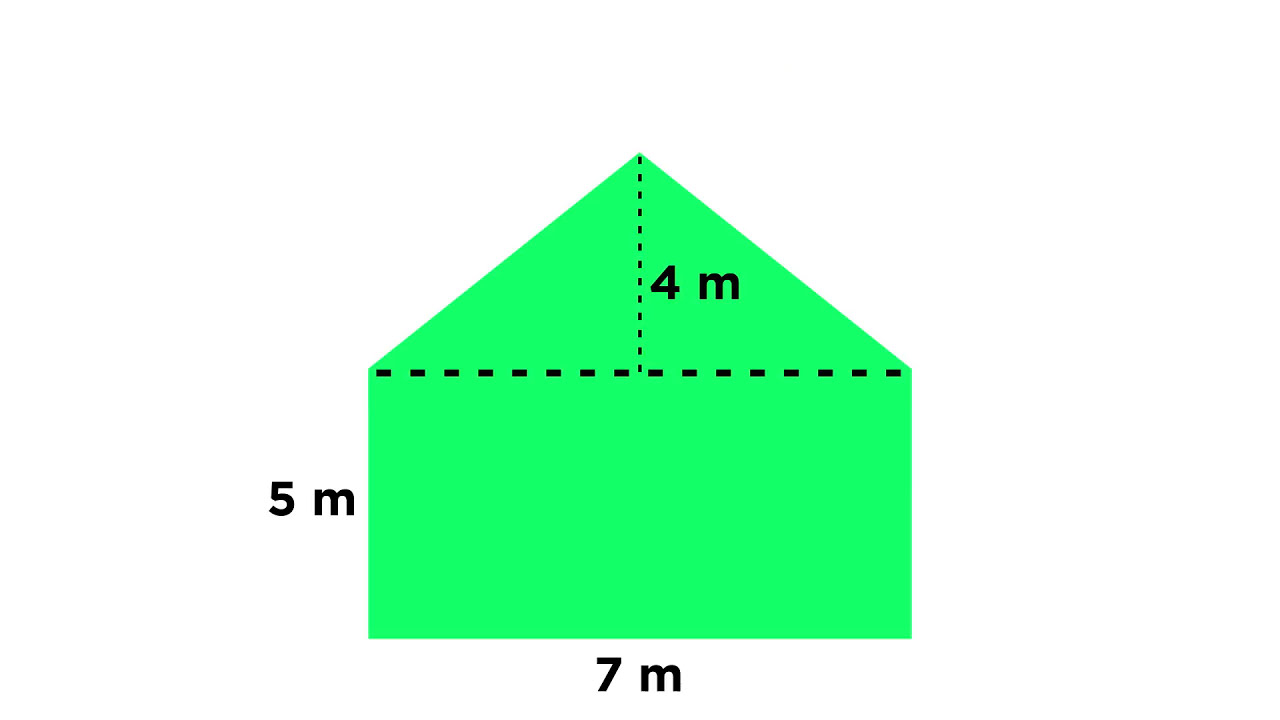
Professor Gist begins Lecture 30 by transitioning from classical mathematical tools to applications of the definite integral, starting with simple area formulas. He emphasizes that instead of memorizing numerous formulas, there is a fundamental concept that area is the integral of the area element, 'da'. The lecture revisits classical area formulas for shapes like rectangles, parallelograms, triangles, and circles, explaining their validity through the integral of the corresponding area elements. The professor uses the parallelogram as an example to demonstrate how slicing it into horizontal strips and integrating these strips can lead to the area calculation. He also introduces the concept of shearing a parallelogram to form a rectangle, which preserves the area element, and applies a similar approach to the area of a triangle.

Continuing the discussion on area calculation, the script delves into more complex shapes and introduces the concept of the Gini Index, an economic measure of income inequality. The area of a circular disc is revisited, this time using different methods to calculate it, such as considering angular variables and radial variables, leading to the integral of area elements. The script explains how the area can be determined by integrating half the product of the radius and the differential angle, or by considering the circumference times the thickness of an infinitesimally thin anulus. The Gini Index is introduced as the ratio of the area between the actual income distribution and an even distribution to the area of the triangle formed by an even distribution, which is a measure of economic disparity within a population.

The script provides a practical example of calculating the Gini Index using a power law distribution model for income. It explains how to integrate the difference between the polynomial distribution and the even distribution from 0 to 1, and then double the result to find the Gini Index. The example shows that if the income distribution followed a cubic monomial, the Gini Index would be calculated by a specific integral, resulting in a value that reflects the deviation from an equitable income distribution. The script also references real economic data, mentioning that in 2010, New York State had a Gini Index of approximately 1/2, suggesting a significant income disparity.

In the final paragraph, the script reflects on the importance of revisiting classic area formulas to deepen understanding and prepare for tackling more complex planar shapes in future lessons. It emphasizes that while students may already be familiar with the formulas for areas of triangles and circles, the lecture serves to reinforce the foundational concept that these areas can be derived from the integral of area elements. The professor hints at the upcoming challenges of calculating areas of more intricate shapes, setting the stage for advanced topics in calculus.