How to choose an appropriate statistical test
TLDRThis lecture guide explores the process of selecting the most suitable statistical test for a study, emphasizing the importance of understanding the research question, data type, and assumptions for parametric tests. It explains the distinction between comparing differences between groups and investigating relationships between variables, and how to determine the scale of measured variables. The lecture also discusses the decision between parametric and non-parametric tests based on data distribution and robustness against extreme values. Furthermore, it covers various study designs, such as paired and unpaired, and introduces appropriate statistical tests for each scenario, including t-tests, ANOVA, chi-square tests, and correlation analyses. The guide concludes with a reminder that the choice of test can depend on the researcher's perspective and the specific context of the data.
Takeaways
- 🔍 The selection of a statistical test depends on the research question, type of data, assumptions for parametric tests, experimental design, and the number of groups.
- 📊 To compare differences between two groups, consider the type of variables (continuous or ordinal) and whether the data meets the assumptions for parametric tests.
- 📈 Parametric tests generally have higher statistical power than non-parametric tests if the assumptions of normality and numericality are met.
- 🌟 If the data is symmetric and fairly normal, even small samples can meet the normality assumption due to the Central Limit Theorem.
- 🚫 Skewed distributions may require larger sample sizes (>30) to meet normality assumptions, or else non-parametric tests are more appropriate.
- 📌 Non-parametric tests are robust against extreme values and are a better alternative when extreme values cannot be removed from the data.
- 🔗 Determine the study design (paired or unpaired) to select the appropriate test for comparing differences or analyzing relationships.
- 💡 Paired study designs reduce variability by comparing differences between similar individuals, such as before and after treatments.
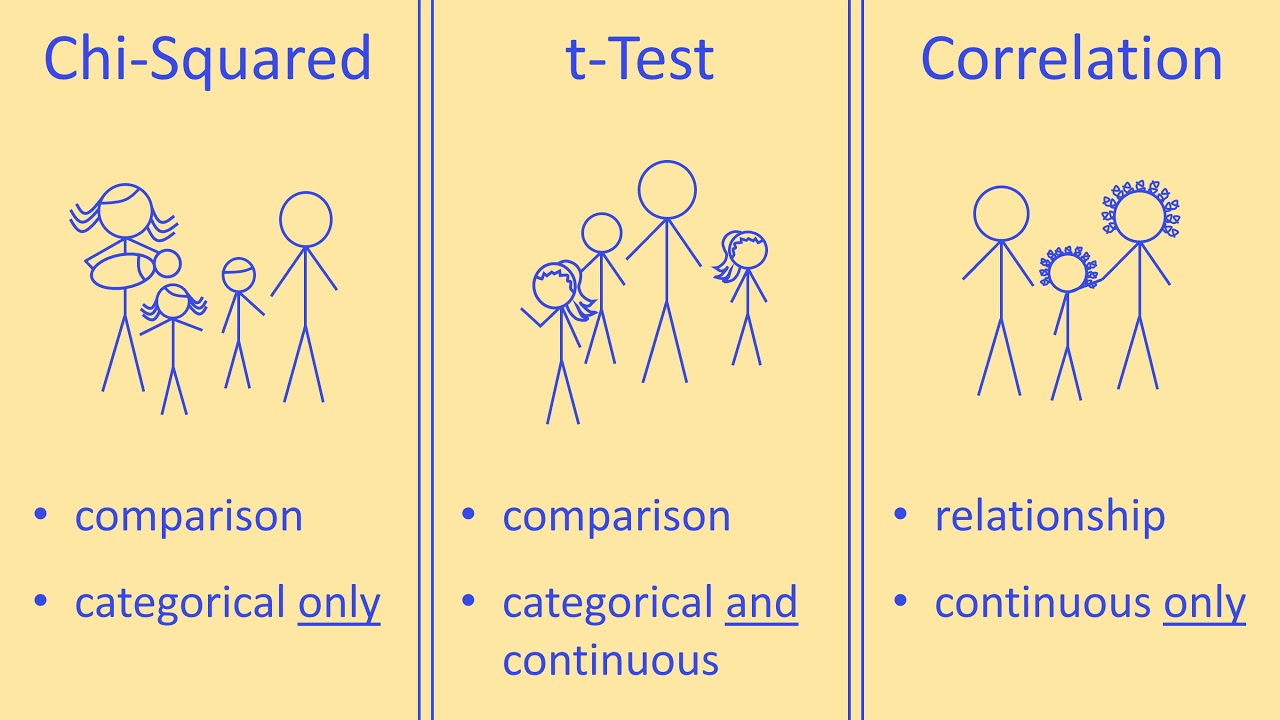
- 📊 For comparing two proportions or investigating relationships between two variables, the chi-square test can be used, while Fisher's test serves as an alternative when expected frequencies are low.
- 🔄 Correlation analysis (Pearson or Spearman) and linear regression are used to analyze relationships between continuous variables, with the latter allowing for prediction and control of external factors.
- 🧐 The choice between parametric and non-parametric tests can be subjective and may vary depending on the researcher's perspective and the specific context of the study.
Q & A
What factors should be considered when choosing an appropriate statistical test for a study?
-The selection of a statistical test depends on the research question, the type of data (scalar or ordinal), assumptions for parametric tests, experimental design, and the number of groups involved.
What is the difference between comparing differences between groups and investigating relationships between variables?
-Comparing differences between groups involves looking at the variation in outcomes, such as growth or performance, between different groups. Investigating relationships between variables, on the other hand, is about understanding how two variables are associated or correlated with each other.
What are continuous and ordinal scales in statistical terms?
-Continuous variables are numeric and can be measured with instruments, such as body weight or blood pressure. Ordinal scales consist of ordered categories, like grades (A to F) or pain scores (1 to 10), where the order reflects a natural progression.
Why should we consider the normal distribution when selecting a parametric test?
-Parametric tests rely on certain distributions, typically the normal distribution, to estimate the likelihood of observed results. If the data is fairly symmetric and appears to be normally distributed, parametric tests are generally more powerful and should be selected.
What is the significance of extreme values in statistical tests?
-Extreme values, or outliers, can significantly affect the results of parametric tests, which are sensitive to such values. In cases where outliers cannot be removed, non-parametric tests are preferred due to their robustness against extreme values.
What are paired and unpaired study designs?
-Paired study designs involve comparing data from the same subjects before and after a treatment or under different conditions. Unpaired designs, on the other hand, compare data from independent subjects or groups, such as different individuals or plants.
What statistical tests can be used for paired and unpaired study designs with continuous data?
-For paired designs, a paired t-test or repeated measures ANOVA can be used if the assumptions of normality are met. For unpaired designs, an independent samples t-test or one-way ANOVA is appropriate, depending on the number of groups and the fulfillment of normality assumptions.
What non-parametric tests are suitable for ordinal data or when normality assumptions are not met?
-For ordinal data or when normality assumptions are not met, non-parametric tests like the Wilcoxon signed-rank test for paired data, the Mann-Whitney U test for independent samples, and the Kruskal-Wallis test for more than two independent groups can be used.
How can we analyze the relationship between two variables with numeric data?
-To analyze the relationship between two numeric variables, we can use the Pearson correlation if the assumptions are met, or the Spearman correlation if the data is not normally distributed or has an ordinal scale.
What tests can be used to compare a sample against a known distribution or population mean?
-To compare a sample against a known distribution or population mean, we can use the chi-square goodness of fit test for frequency distributions and the one-sample t-test or one-sample Wilcoxon sign rank test for continuous data, depending on the fulfillment of normality assumptions.
How does the selection between parametric and non-parametric tests vary among researchers?
-The selection between parametric and non-parametric tests can vary among researchers based on their interpretation of the data and the assumptions they believe are met. For instance, a simple linear regression model might be used instead of an unpaired t-test in some cases, especially when controlling for external factors.
Outlines
📊 Introduction to Selecting Statistical Tests
This paragraph introduces the process of selecting the most appropriate statistical test for a study. It emphasizes that the choice between different tests depends on the research question, the type of data, assumptions for parametric tests, experimental design, and the number of groups involved. The speaker outlines the initial decision-making process, which involves determining whether the goal is to compare differences between groups or to investigate relationships between variables. The paragraph also discusses the importance of understanding the scale of measured variables and the implications for choosing between parametric and non-parametric tests.
🧬 Study Design and Test Selection
The second paragraph delves into the specifics of study design, differentiating between paired and unpaired study designs. It provides examples of each, such as assigning plants to different fertilizers (independent) or matching individuals based on weight and gender for a drug treatment (paired). The paragraph explains how the design influences the choice of statistical tests, mentioning paired t-tests, repeated measures ANOVA, and non-parametric alternatives like the Wilcoxon signed-rank test for paired designs, and unpaired t-tests or one-way ANOVA for independent groups. It also touches on the use of non-parametric tests like the Friedman test when assumptions for parametric tests are not met.
📈 Non-Parametric Tests and Their Applications
This paragraph focuses on non-parametric tests, which are robust alternatives when data does not meet the assumptions for parametric tests. It discusses the use of the Wilcoxon Mann-Whitney test (equivalent to the unpaired t-test), the Kruskal-Wallis test (for more than two independent groups), and the chi-square test for comparing proportions or independence between two categorical variables. The paragraph also mentions Fisher's exact test as an alternative when expected frequencies are low. It further explains the use of McNemar's test and Cochrane's Q test for paired designs and extends the discussion to correlation and regression analyses for continuous variables, highlighting the Pearson and Spearman correlations, and linear regression versus correlation analysis.
🥼 Practical Examples of Test Selection
The final paragraph provides practical examples to illustrate the selection of appropriate statistical tests. It covers scenarios like comparing white blood cell concentration between healthy and diseased individuals (unpaired t-test), evaluating the effect of a fertilizer on plant growth using a paired design (Wilcoxon signed-rank test), and analyzing the weight of fish species across different lakes (one-way ANOVA or Kruskal-Wallis test). It also discusses examining the relationship between smoking and lung cancer (chi-square test) and the correlation between systolic blood pressure and body mass index (Pearson or Spearman correlation). The paragraph concludes with a reminder that the choice of test can be subjective and that there are many more statistical tests available beyond the basic ones covered in the lecture.
Mindmap
Keywords
💡Statistical Test
💡Parametric Test
💡Non-Parametric Test
💡Experimental Design
💡Continuous Variables
💡Ordinal Scale
💡Normal Distribution
💡Skewed Distribution
💡Chi-Square Test
💡Correlation
💡Regression
Highlights
The lecture discusses how to choose the most appropriate statistical test for a study based on the research question, data type, assumptions for parametric tests, experimental design, and number of groups.
Comparing differences between two groups or investigating relationships between variables are the two main objectives that guide the selection of statistical tests.
Continuous variables, such as body weight and blood pressure, are numeric and measured with instruments, while ordinal variables like grades or pain scores have ordered categories.
Parametric tests, which rely on the normal distribution, are generally more powerful than non-parametric tests but require data to meet certain assumptions.
The normality assumption can be fulfilled even for small samples if the data is fairly symmetric, according to the central limit theorem.
Skewed distributions may require larger sample sizes or non-parametric tests, which are more robust against extreme values.
Paired and unpaired study designs are distinguished by whether the subjects are matched or assigned independently to treatment conditions.
Repeated measures ANOVA is used when multiple measurements are taken on the same individual over time, while a paired t-test is used for comparing differences between two paired groups.
Non-parametric alternatives to parametric tests include the Wilcoxon signed-rank test for paired designs and the Mann-Whitney U-test for unpaired designs.
The Kruskal-Wallis test is a non-parametric alternative to one-way ANOVA for comparing more than two independent groups.
Chi-square tests are used to compare proportions or test for independence between categorical variables.
Fisher's exact test is an alternative to the chi-square test when expected frequencies in a contingency table are less than five.
The McNemar's test and Cochran's Q test are used for analyzing changes within paired samples across multiple treatments.
Pearson and Spearman correlations are used to analyze the strength and direction of relationships between continuous or ordinal variables.
Linear regression is used to predict or estimate the effect of one variable on another, requiring the specification of dependent and independent variables.
One-sample tests, such as the one-sample t-test or the Wilcoxon sign rank test, are used to compare a sample mean or proportion to a population value.
Chi-square goodness of fit tests are used to compare observed frequency distributions to known or hypothesized distributions.
The selection between parametric and non-parametric tests can be subjective and may vary depending on the researcher's perspective and the specific context of the data.
Advanced regression models are becoming increasingly popular for their ability to control for external factors and provide more nuanced statistical analyses.
Transcripts
Browse More Related Video
Choosing a Statistical Test for Your IB Biology IA

Statistics made easy ! ! ! Learn about the t-test, the chi square test, the p value and more

One sample t-test vs Independent t-test vs Paired t-test

t-Test - Full Course - Everything you need to know

Bootstrap Hypothesis Testing in R with Example | R Video Tutorial 4.4 | MarinStatsLecutres

How to Use SPSS: Choosing the Appropriate Statistical Test
5.0 / 5 (0 votes)
Thanks for rating: