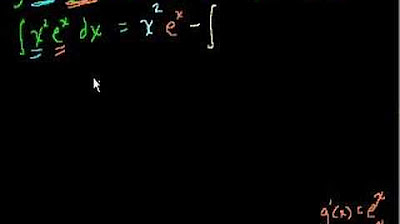Doing the World's Hardest Integral (joke video)
TLDRIn this video, Chris tackles the challenging integral of x to the power of e^x, transforming it into a double integral and utilizing Damares' theorem to simplify the expression. He creatively blends math with a fantastical journey to ancient Mesopotamia, where he humorously exploits a video game-like glitch to bypass obstacles and obtain a rare textbook containing the solution. The video is an entertaining mix of math and storytelling, encouraging viewers to expand their integration skills.
Takeaways
- 📚 The video discusses the importance of integrals in math and physics, emphasizing their frequent use in problem-solving.
- 🧠 The speaker tries to do one or two integrals daily to maintain proficiency, suggesting a regular practice approach for viewers.
- 🌟 The video aims to teach how to compute the indefinite integral of x to the power of e^x, a challenging integral.
- 📈 The strategy involves squaring the integral and rewriting it as a double integral over x and y, drawing parallels with the integral of a Gaussian.
- 🔄 A substitution method is used with u = e^x and v = e^y, to simplify the exponential terms in the integral.
- 📜 Demare's Theorem is introduced for simplifying the integral, which is applicable to monotonic functions taken to the exponent of their argument.
- 🤔 The video humorously references a fictional scenario involving a rare textbook in the catacombs beneath a ziggurat, adding a playful narrative.
- 🎮 The speaker alludes to video game strategies like clipping through walls and exploiting glitches, as a metaphor for solving complex math problems.
- 🛍 The video concludes with the speaker having the integral in the correct form and the location of the solution, encouraging viewers to perform the integral.
- 👽 The content is presented in a creative and engaging manner, combining math education with a fantasy adventure theme.
- 🤓 The video ends with a tongue-in-cheek comment on the peculiarity of enjoying integrals, adding a touch of humor to the educational content.
Q & A
What is the main topic of the video?
-The main topic of the video is how to compute the indefinite integral of x to the power of e to the x.
Why does the video creator do one or two integrals every day?
-The video creator does one or two integrals every day to stay sharp in math and physics.
How does the video start the process of solving the integral?
-The video starts by squaring the integral and rewriting it as a double integral over x and y.
What is the significance of squaring the integral in this context?
-Squaring the integral allows for the calculation of a double integral, which can simplify the process of computing the original single integral.
What substitution is used in the video to simplify the integral?
-The video uses the substitution where u equals e to the x and v equals e to the y, with dx equals one over u du and dy equals one over v dv.
What theorem is applied to simplify the integral further?
-D'Alembert's theorem is applied to simplify the integral by replacing the function with the reciprocal of its adjoint.
Why is D'Alembert's theorem not commonly taught in standard calculus classes anymore?
-D'Alembert's theorem has been less frequently taught over the last decade or so, though it was once a standard part of calculus curriculums.
What is the significance of the Baker-Naukbauer type of integral in the video?
-The Baker-Naukbauer type of integral is significant because it allows the integral to be solved using known methods, avoiding the need to convert it into an infinite series.
What is the role of the textbook in the catacombs beneath the ziggurat?
-The textbook in the catacombs is the only known source with the solution to the specific integral problem discussed in the video.
How does the video creator humorously suggest accessing the textbook?
-The video creator humorously suggests traveling to ancient Mesopotamia, focusing on the water deity Aya, and using a video game-like glitch to access the room containing the textbook.
What is the final result of the video?
-The final result of the video is that the integral is in the correct form, and the creator has access to the textbook that provides the solution, implying that the integral can now be solved.
Outlines
📚 Introduction to Integrals and the Challenge Ahead
The video begins with the host, Chris, emphasizing the importance of integrals in mathematics and physics. He shares his personal practice of solving integrals daily to maintain his skills. The main challenge of the video is to tackle the indefinite integral of x to the power of e to the x, a complex problem that Chris promises to break down step by step. The goal is to equip viewers with new skills for their integration toolbox. The first step involves squaring the integral and rewriting it as a double integral over x and y, drawing parallels to the Gaussian integral and its relation to pi.
Mindmap
Keywords
💡integrals
💡double integral
💡substitution
💡D'Alembert's theorem
💡hyperbolic tangent
💡Baker-Naudé-Baker (BNB) integral
💡textbook
💡King Gilgamesh
💡gaming references
💡Gilgamesh skip
💡calculus
💡mathematical techniques
Highlights
The importance of integrals in math and physics is emphasized.
The speaker does one or two integrals daily to maintain proficiency.
The video aims to teach how to do the indefinite integral of x to the power of e^x.
The process starts by squaring the integral and rewriting it as a double integral over x and y.
The integral of a Gaussian is mentioned as an example of a similar technique.
A substitution is performed with u = e^x and v = e^y.
D'Alembert's theorem is introduced as a key tool for simplifying the integral.
The theorem allows replacing a monotonic function with its adjoint's reciprocal.
The integral is transformed into a Baker-Nauenberg type of the second kind.
A textbook with the solution exists but is metaphorically located in ancient Mesopotamia.
The speaker humorously references a video game strategy to access the textbook.
The video combines math with a fantastical narrative involving King Gilgamesh.
A glitch called 'Gilgamesh Skip' is mentioned, discovered by a Twitch streamer.
The integral is left in its final form, ready for actual computation.
The video concludes with a reminder of the enjoyment of doing integrals.
The speaker's unique approach to explaining integrals is both educational and entertaining.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: