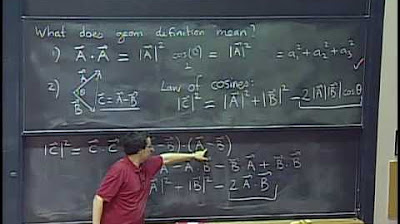8.01x - Lect 3 - Vectors - Dot Products - Cross Products - 3D Kinematics
TLDRIn this engaging lecture, the professor introduces the concept of vectors, explaining scalars and vectors in physics with practical examples. The discussion delves into the addition, subtraction, and decomposition of vectors, emphasizing their applications in understanding complex physical phenomena. The lecture also covers the dot product and cross product of vectors, highlighting their significance in physics. The professor uses relatable examples and demonstrations to clarify these concepts, making the subject matter accessible and intriguing.
Takeaways
- 📚 Vectors are mathematical objects with both magnitude and direction, represented by arrows.
- 🔄 The addition and subtraction of vectors can be performed using the head-tail technique or the parallelogram method.
- 🔢 Scalars are quantities that have only magnitude and no direction, such as mass, temperature, and speed.
- 📈 The dot product (scalar product) of two vectors is a scalar value that can be calculated using the magnitudes and the cosine of the angle between the vectors.
- ✖️ The cross product (vector product) of two vectors results in a new vector that is perpendicular to both original vectors and follows the right-hand rule for direction.
- 📊 The magnitude of a vector is found by taking the square root of the sum of the squares of its components.
- 🌟 The decomposition of a vector into its component parts along the x, y, and z axes allows for the analysis of motion in three-dimensional space.
- 🚀 In projectile motion, the horizontal and vertical components of velocity and acceleration can be analyzed independently.
- 🎾 The independence of horizontal and vertical motion is demonstrated by the ability to catch a ball thrown horizontally after it has been launched vertically.
- 📐 The position, velocity, and acceleration of an object in three-dimensional space can be described by a system of equations for each axis.
- 🧮 Negative vectors are represented by flipping a vector 180 degrees, which is equivalent to changing the sign of one of its components when using the coordinate system.
Q & A
What are scalars in physics?
-Scalars are quantities in physics that are determined uniquely by one number. Examples of scalars include mass, temperature, and speed.
What is the difference between a scalar and a vector?
-A scalar has only magnitude and no direction, whereas a vector has both magnitude and direction, which is why vectors are often represented by arrows.
How are vectors added together?
-Vectors are added using two main methods: the 'head-tail' technique, where the tail of the second vector is placed at the head of the first, and the 'parallelogram method', where the tails of both vectors are placed together and the parallelogram is completed.
What is the significance of the direction in vectors?
-The direction in vectors is significant because it indicates the orientation of the vector in space. This is crucial for understanding physical quantities like velocity and acceleration, which depend on both magnitude and direction.
What is the meaning of a negative vector?
-A negative vector is the same as the original vector but flipped over 180 degrees. It represents the vector in the opposite direction.
How is the magnitude of a vector calculated?
-The magnitude of a vector is calculated as the square root of the sum of the squares of its components along each axis (x, y, and z).
What is the dot product of two vectors?
-The dot product of two vectors is a scalar quantity that is calculated by multiplying the corresponding components of the two vectors and then summing these products.
What is the significance of the dot product in physics?
-The dot product is significant in physics because it can be used to calculate work done by a force, which is a scalar quantity. The dot product also indicates the angle between two vectors.
What is the cross product of two vectors?
-The cross product of two vectors is a vector that is perpendicular to both of the original vectors. It is denoted by a cross symbol and its direction is determined by the right-hand rule.
How does the cross product relate to the direction of vectors?
-The cross product results in a vector that is perpendicular to both of the original vectors. The direction of the cross product can be determined by the right-hand rule, which states that if you point your right hand in the direction of one vector and curl your fingers towards the second vector, your thumb will point in the direction of the cross product.
How can the motion of a particle in three-dimensional space be analyzed?
-The motion of a particle in three-dimensional space can be analyzed by decomposing the motion into its components along the x, y, and z axes. Each component can be treated as an independent one-dimensional motion, simplifying the analysis.
What is the practical application of decomposing motion into components?
-Decomposing motion into components allows for a simpler and more manageable analysis of complex motions, such as the trajectory of a projectile. It helps in understanding the independent behaviors of the motion along different axes and can be used to predict the future position, velocity, and acceleration of the particle.
Outlines
📚 Introduction to Vectors and Scalars
The paragraph introduces the concept of scalars and vectors in physics. Scalars, such as mass, temperature, and speed, are quantities described by a single number. Vectors, on the other hand, have both magnitude and direction and are represented by arrows. The example of velocity and acceleration as vectors is given, with a detailed explanation of how vectors are added using the 'head-tail' technique and the 'parallelogram method.' The concept of negative vectors is also briefly touched upon.
🔄 Vector Addition and Subtraction
This section delves deeper into vector operations, focusing on the addition and subtraction of vectors. It explains the 'head-tail' technique for vector addition and introduces the concept of negative vectors as being the same as the original vector but flipped 180 degrees. The method for vector subtraction is also discussed, where subtracting a vector is equivalent to adding its negative. The paragraph emphasizes the difference in complexity between scalar and vector arithmetic, especially when dealing with vector decomposition.
📐 Decomposing Vectors in 3D Space
The paragraph discusses the decomposition of vectors in three-dimensional space. It explains how a vector can be projected onto the x, y, and z axes and how these projections can be represented by unit vectors. The concept of unit vectors is introduced, and the paragraph shows how a vector can be expressed as a sum of its components along the axes. The magnitude of a vector is defined as the square root of the sum of the squares of its components. The paragraph also touches on the concept of vector angles and how they relate to the vector's components.
🤝 Dot Product and Vector Multiplication
This section introduces the dot product, also known as the scalar product, as a method of multiplying two vectors. Two methods for calculating the dot product are presented: one using the components of the vectors and another using the magnitudes of the vectors and the cosine of the angle between them. The paragraph explains the implications of the dot product being positive, zero, or negative, and how it relates to the angle between the vectors. The concept of work in physics is briefly mentioned as being related to the dot product.
🔄 Cross Product and Vector Direction
The paragraph introduces the cross product, another method of vector multiplication, and provides two methods for calculating it. The first method involves using a determinant of a matrix with vector components, while the second method relates to the magnitudes of the vectors and the sine of the angle between them. The direction of the cross product is explained using a right-handed coordinate system and the 'corkscrew rule.' The section emphasizes the importance of using a consistent coordinate system and the applications of cross products in physics.
🚀 Three-Dimensional Motion of a Particle
This section discusses the motion of a particle in three-dimensional space. The vector r, representing the position of the particle, is described as a function of time and decomposed into its x, y, and z components. The concepts of velocity and acceleration are introduced as the first and second derivatives of the position vector, respectively. The paragraph highlights the advantage of decomposing complex three-dimensional motion into simpler one-dimensional motions along each axis.
🏌️ Decomposition in One-Dimensional Motions
The paragraph further elaborates on the decomposition of motion into one-dimensional components. It explains how a complex motion can be broken down into independent motions along the x and y axes. The example of a thrown object is used to demonstrate how the x and y components of motion are independent of each other. The section concludes with a practical demonstration of the concept, showing that the x component of velocity remains constant while the y component changes due to gravity.
🎯 Experiment Demonstrating Independent Motion
The final part of the script describes an experiment that visually demonstrates the independent nature of horizontal and vertical motion. A golf ball is launched from a device that also moves horizontally, and if executed correctly, the ball should return to the same point from which it was launched. The experiment aims to illustrate that the horizontal motion is constant and independent of the vertical motion, which is affected by gravity. The script ends with a successful demonstration of the experiment, reinforcing the concept of decomposing motion into its horizontal and vertical components.
Mindmap
Keywords
💡Scalars
💡Vectors
💡Head-Tail Technique
💡Parallelogram Method
💡Decomposition of Vectors
💡Dot Product
💡Cross Product
💡Unit Vectors
💡Acceleration
💡Projectile Motion
Highlights
Introduction to scalars and vectors in physics, explaining that scalars are quantities determined by one number while vectors require both magnitude and direction.
Explanation of how vectors are represented by arrows, with the convention of a dot indicating the head-on view and a cross for the view from behind.
Discussion on adding vectors using the 'head-tail' technique and the 'parallelogram method', emphasizing that the order of addition does not matter for vectors.
Clarification on the concept of negative vectors, showing that subtracting a vector from itself results in zero, and introducing the idea of a vector flipped 180 degrees.
Explanation of vector subtraction, showing that A minus B is equivalent to A plus negative B, and how to visualize this using the head-tail technique.
Introduction to the decomposition of vectors, projecting them onto the x, y, and z axes, and the use of unit vectors in this process.
Rewriting of a vector in terms of its components along the x, y, and z axes, using unit vectors and the concept of vector projection.
Calculation of the magnitude of a vector using the Pythagorean theorem, with an example given to illustrate the process.
Explanation of the dot product of two vectors, including its definition as a scalar and the formula for calculating it using the components of the vectors.
Introduction to the concept of the cosine of the angle between two vectors, and how it relates to the magnitude of the vectors and their dot product.
Discussion on the sign of the dot product and its implications, such as positive work, negative work, and the relationship with the angle between the vectors.
Introduction to the cross product, or vector product, of two vectors, including its notation and the method for calculating it using a matrix.
Explanation of the geometrical interpretation of the cross product, including the magnitude and direction determined by the sine of the angle between the vectors.
Demonstration of the right-hand rule for determining the direction of the cross product, and the importance of using a right-handed coordinate system.
Presentation of the equations for a moving particle in three-dimensional space, decomposing the motion into components along the x, y, and z axes.
Illustration of how the decomposition of motion into its components can simplify the analysis of complex trajectories, such as the motion of a thrown object.
Experiment demonstrating the independent motion in the x and y directions, using a golf ball fired vertically and horizontally to show the separation of motion components.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: