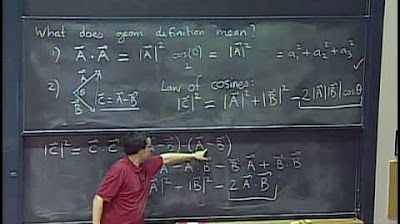Everything You Need to Know About VECTORS
TLDRThis script introduces the concept of vectors and coordinate systems, explaining how points and vectors are represented in two dimensions. It delves into vector properties such as length and direction, and how they can be manipulated through scalar operations. The video also explores vector operations, including addition, subtraction, and the calculation of the distance between points. Further, it explains the dot product and cross product of vectors, their applications, and how they relate to the angle between vectors. The content is presented in an engaging and informative manner, suitable for learners at various levels.
Takeaways
- 📐 Coordinate systems in two dimensions consist of an x-axis (horizontal) and y-axis (vertical), with points on the system given by (x, y) coordinates.
- 📍 Vectors are represented by arrows and are defined by their length (magnitude) and direction, differing from points which have a specific position.
- 🔄 Vector components are determined by the number of steps a vector moves in the x (horizontal) and y (vertical) directions from its initial position.
- 📈 Scalar operations involve multiplying or dividing every component of a vector by a scalar (number), resulting in a new vector that is scaled in size.
- 🔢 Vector operations include addition and subtraction, where the sum or difference of two vectors is calculated by adding or subtracting their respective components.
- 📊 The length (magnitude) of a vector is calculated using the Pythagorean theorem, and is represented by the symbol ||v||.
- 🏷 Unit vectors are special vectors with a length of one, pointing in a specific direction; they are used to express vectors in terms of their components along coordinate axes.
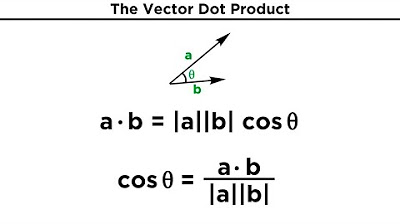
- 🤝 The dot product (scalar product) of two vectors is a scalar value calculated using the formula |a||b|cos(θ), where θ is the angle between the vectors.
- ✖️ The cross product (vector product) of two vectors results in a new vector that is perpendicular to the original vectors and is defined in three dimensions.
- 🔄 The direction of the cross product can be determined using the right-hand rule, and its length can be calculated as |a||b|sin(θ), where θ is the angle between the vectors.
- 🔄 The cross product is zero if vectors are parallel and equal to the product of their magnitudes if they are perpendicular.
Q & A
What are the two lines that make up a two-dimensional coordinate system?
-A two-dimensional coordinate system is made up of a horizontal line called the x-axis and a vertical line called the y-axis.
How are coordinates assigned to a point in a coordinate system?
-Coordinates are assigned to a point by tracing a line parallel to the y-axis onto the x-axis for the x-coordinate and a line parallel to the x-axis onto the y-axis for the y-coordinate.
What is the order of coordinates for a point in a two-dimensional coordinate system?
-The order of coordinates for a point is written with the x-coordinate first and then the y-coordinate.
What is the origin in a coordinate system and what are its coordinates?
-The origin is the point where the x and y axes cross. It is often denoted by the letter O and has coordinates (0, 0).
How are vectors represented in a coordinate system?
-Vectors are represented by arrows, defined by their lengths and directions. They do not have a fixed position and can be moved anywhere in the coordinate system.
How are the components of a vector calculated?
-The components of a vector are calculated by determining how many steps the vector goes left or right (for the x-component) and how many steps it goes up or down (for the y-component).
What is scalar multiplication of a vector?
-Scalar multiplication of a vector involves multiplying every component of the vector by a scalar (a number), which can result in stretching or shrinking the vector accordingly.
What is the formula for calculating the length (magnitude) of a two-dimensional vector?
-The length (magnitude) of a two-dimensional vector is calculated using the Pythagorean theorem: √(x^2 + y^2), where x and y are the components of the vector.
What is a unit vector and how is it represented?
-A unit vector is a vector with a length of one. It points in the same direction as the original vector but has a length of 1. It is represented with a hat ( caret ) symbol above the vector's name.
How is the dot product of two vectors calculated and what does it represent?
-The dot product of two vectors is calculated using the formula a·b = |a|*|b|*cos(θ), where |a| and |b| are the magnitudes of the vectors and θ is the angle between them. The dot product is a scalar and represents the projection of one vector onto the other.
What is the cross product of two vectors and how is it visualized?
-The cross product of two vectors results in another vector that is perpendicular to the original vectors. It is visualized using the right-hand rule, where the thumb points in the direction of the cross product when the index and middle fingers point in the directions of the original vectors.
Outlines
📐 Introduction to Coordinate Systems and Vectors
This paragraph introduces the concept of coordinate systems in two dimensions, explaining the roles of the x-axis and y-axis, and how points are assigned coordinates based on their positions within this system. It also differentiates between points and vectors, emphasizing that vectors do not have a fixed position and are represented by arrows. The explanation continues with how to calculate the x and y components of a vector and introduces the notation for two-dimensional vectors. The paragraph concludes with a brief mention of three-dimensional vectors and the potential for n-dimensional vectors, setting the stage for further discussion on scalar operations.
🔢 Scalar Operations with Vectors
The second paragraph delves into scalar operations, which involve a vector and a number (scalar). It explains that scalar operations can be either multiplication or division, with scalar multiplication being the primary focus. The process of scalar multiplication is described, where every component of the vector is multiplied by the scalar, resulting in a new vector that is scaled by a factor corresponding to the scalar. The paragraph also touches on the special case of multiplying by -1, which results in a vector pointing in the opposite direction. The concept of vector length, or magnitude, is introduced, along with the Pythagorean theorem as it applies to calculating the length of a vector. Additionally, the concept of unit vectors is briefly mentioned, highlighting their role in vector notation.
🤝 Vector Operations: Addition and Subtraction
This paragraph discusses vector operations, specifically vector addition and subtraction. It explains how to calculate the sum or difference of two vectors by adding or subtracting their respective x and y components. The paragraph provides a visual example of how to physically add two vectors by moving one vector's tail to the tip of the other and using the resulting vector from the original vector's tail to the tip of the second vector. The concept of vector length and the distance between two points using vector subtraction is also covered. The paragraph then introduces the dot product and scalar product as alternative names for the same operation, and explains how the dot product is calculated and its relationship with the angle between two vectors. The properties of the dot product, including its dependence on the angle between vectors and its use as a measure of vector similarity, are discussed in detail.
🤲 Cross Product and Vector Perpendicularity
The final paragraph focuses on the cross product, another way to multiply two vectors, which results in a new vector. It explains the cross product's definition and calculation using the determinant of a matrix, and how it differs from the dot product in that it is only defined in three dimensions. The paragraph describes the properties of the cross product, including its dependence on the angle between vectors and its use as a measure of vector perpendicularity. The right-hand rule is introduced as a visual tool for understanding the direction of the cross product. The length of the cross product is discussed in relation to the lengths of the original vectors and the angle between them. The paragraph concludes with a mention of the cross product's special properties, such as its result being zero if the vectors are parallel and equal to the product of the vector lengths if they are perpendicular. The video script ends with a summary of the key points and an invitation to support further content creation.
Mindmap
Keywords
💡Coordinate Systems
💡Vectors
💡Components
💡Scalar Operations
💡Vector Addition and Subtraction
💡Length of a Vector
💡Unit Vector
💡Dot Product
💡Cross Product
💡Unit Vector Notation
Highlights
Introduction to coordinate systems in two dimensions, consisting of a horizontal x-axis and a vertical y-axis.
Explanation of how to assign coordinates to a point P in the coordinate system by using parallel lines to the axes.
Description of the origin point O, where the x and y axes cross, with coordinates (0,0).
Transition from coordinate systems to vectors, emphasizing that vectors do not have a position and are represented by arrows.
Definition of vector components, which are calculated based on the steps a vector moves left/right (x-component) and up/down (y-component).
Illustration of how to calculate the components of vector B, including steps to the left (negative x-component) and up (positive y-component).
Explanation of the notation used for two-dimensional vectors with components enclosed in square brackets, and the extension to three and n-dimensional vectors.
Discussion of scalar operations, specifically scalar multiplication, where each component of a vector is multiplied by a scalar value.
Visual representation of scalar multiplication, showing how a vector is scaled by a factor of three when multiplied by a scalar.
Special case of scalar multiplication with a value of negative one, resulting in a vector pointing in the opposite direction.
Introduction to vector operations, including addition and subtraction, with a focus on how to calculate the sum of two vectors.
Visualization of vector addition by moving vector B's tail to the tip of vector A, resulting in a new vector from A's tail to B's tip.
Explanation of vector subtraction, which can be used to calculate the vector from one point to another, and its relation to the distance between points.
Discussion of the length (magnitude or norm) of a vector, represented by two vertical bars, and its calculation using the Pythagorean theorem.
Introduction to unit vectors, which are vectors of length one and are used to define the direction of other vectors.
Alternative way to write vectors using unit vector notation, which is the sum of components multiplied by the respective unit vector.
Explanation of the dot product (scalar product) of two vectors, its formula, and its geometric interpretation as the product of the lengths of the vectors and the cosine of the angle between them.
Visualization of the dot product and its dependency on the angle between the vectors, with special cases for zero, 90, and 180-degree angles.
Introduction to the cross product (vector product), its definition, and its dependency on the determinant of a matrix, with a focus on its three-dimensional nature.
Explanation of the right-hand rule for visualizing the direction of the cross product and its properties related to the angle between the vectors.
Conclusion that the cross product measures the perpendicularity of two vectors, in contrast to the dot product which measures their parallelism.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: