Ch 8: Why is probability equal to amplitude squared? | Maths of Quantum Mechanics
TLDRThe video script delves into the Born rule in quantum mechanics, explaining how the probability of a particular outcome is determined by the squared magnitude of the coefficient in an eigenstate expansion. It clarifies that the probability density for continuous observables like position is given by the squared magnitude of the wavefunction. The script also introduces the concept of quantum state collapse upon measurement and sets the stage for further exploration of hermitian and unitary operators, as well as the Schrödinger equation in future episodes.
Takeaways
- 📐 The Born Rule: The probability of measuring a particular eigenstate is the square of the amplitude of its coefficient in the eigenbasis expansion.
- 🌟 Quantum States: A quantum state represents all possible observables and their associated probabilities, encapsulated in a vector (ket) in Hilbert space.
- 🔄 Eigenbases: Eigenvectors of an observable form an orthonormal basis, allowing quantum states to be expanded in terms of eigenstates of different observables.
- 🎲 Measurement Outcomes: The definite value measured for an observable corresponds to an eigenvector, and the probability of this outcome is given by the Born rule.
- 📈 Probability Calculation: The probability of a measurement outcome is found by taking the inner product with the unit vector in the direction of the eigenvector, and normalizing by the state's length.
- 🔢 Eigenvalue Expansion: Quantum states can be expanded in eigenbases of position, momentum, energy, etc., each representing a superposition of all possible values for the observable.
- 🌀 Superposition: A quantum state can be in a superposition of eigenstates, with coefficients representing the probability of measuring each eigenvalue.
- 🚫 Length of Quantum State: The total length (magnitude) of a quantum state is not necessarily one; it must be normalized to ensure probabilities sum to one.
- 📊 Probability Function: The probability function f must satisfy two conditions: the sum of probabilities for all outcomes equals one, and the length of the quantum state remains constant in any basis.
- 🔍 Intuition and Derivation: The Born rule emerges naturally from considering the length of the vector component along an eigenvector and the need for a probability function that is consistent across different bases.
- 🌐 Continuous Eigenbases: For continuous eigenbases like position, the probability density is given by the squared magnitude of the wavefunction (coefficient) in front of the eigenstate.
Q & A
What is the Born rule in quantum mechanics?
-The Born rule states that the probability of measuring a particular eigenstate is equal to the amplitude squared of its coefficient when the quantum state is expanded in the corresponding eigenbasis. If all quantum states are assumed to have a length of 1, then the probability is simply the coefficient squared.
How do physical observables relate to linear operators in quantum mechanics?
-Physical observables in quantum mechanics are represented by linear operators acting on the Hilbert space where quantum states reside. The eigenvalues of these operators correspond to the possible outcomes of a measurement, and the eigenvectors represent the states where the observable has a definite value.
What is the significance of eigenvectors and eigenvalues in quantum mechanics?
-Eigenvectors represent the definite states of an observable, and eigenvalues correspond to the definite values that can be measured for that observable. The eigenvectors of an observable form an orthonormal basis, allowing any quantum state to be expanded in terms of these eigenbases, which represents a superposition of all possible values for the observable.
How does the quantum state collapse occur in the context of measurement?
-Quantum state collapse happens when a measurement is made on a quantum system. The system transitions from a superposition of states to a definite eigenstate corresponding to the measured eigenvalue. The probability of collapsing into a particular eigenstate is given by the Born rule.
What is the role of the wavefunction in quantum mechanics?
-The wavefunction, which is related to the coefficients in the eigenbasis expansion of a quantum state, provides the probability density for finding a particle in a particular state. It is a crucial concept as it encapsulates all the information needed to calculate probabilities for various outcomes in quantum mechanics.
Why is the magnitude squared of the coefficient used in the Born rule?
-The magnitude squared of the coefficient is used because it represents the probability of a particular outcome. This is derived from the conditions that the probability function must satisfy, including the requirement that the sum of all probabilities must equal one and that the length of the quantum state remains constant in any basis.
How does the Born rule apply to continuous eigenbases?
-For continuous eigenbases, like position, the Born rule gives the probability density as the squared magnitude of the coefficient in front of the eigenstate. This probability density function describes the likelihood of finding the particle at various positions.
What is the significance of the condition that the sum of all probabilities must equal one?
-This condition ensures that the total probability of all possible outcomes of a measurement is 100%, which is a fundamental principle in probability theory and reflects the fact that one of the possible outcomes must occur when a measurement is made.
What is the role of the Schrödinger equation in quantum mechanics?
-The Schrödinger equation is used to describe the time evolution of quantum states. It provides a way to predict how the probabilities and coefficients of an eigenbasis expansion will change over time due to the dynamics of the system.
How does the concept of hermitian operators relate to observables in quantum mechanics?
-Hermitian operators are a special class of linear operators that have real eigenvalues, which correspond to the possible results of physical measurements. In quantum mechanics, observables are represented by hermitian operators because they ensure that the probabilities derived from the eigenvalues are real and positive, as required for physical probabilities.
What is the expectation value of an observable in quantum mechanics?
-The expectation value of an observable, also known as the average value, is calculated by taking the inner product of the quantum state with the eigenvectors of the observable, weighted by the corresponding eigenvalues, and summing over all possible outcomes. This reflects the average result one would expect from a large number of measurements.
Outlines
📐 Quantum Mechanics and Observables
This paragraph introduces the concept of physical observables in quantum mechanics as linear operators and their relationship with eigenvectors and eigenvalues. It sets the stage for understanding the Born rule by discussing the orthonormal eigenbasis and how quantum states can be expanded in terms of these eigenbases, representing superpositions of all possible values for an observable. The paragraph also touches on the idea of probability in quantum mechanics, hinting at the connection between the magnitude of a state's component along an eigenvector and the likelihood of measuring the corresponding eigenvalue.
🧠 Intuition and the Born Rule
The paragraph delves into the Born rule, which quantifies the probability of a particular outcome in quantum mechanics. It explains the initial intuition that the larger the component of a quantum state along an eigenvector, the higher the probability of measuring the corresponding eigenvalue. The paragraph discusses the process of finding the probability of measuring a specific energy value by examining the quantum state's expansion in the energy eigenbasis. It also addresses the limitations of using the absolute value of coefficients as probabilities and introduces the concept of complex number coefficients, leading to the need for a more accurate probability function.
🔄 Resolving Probability Function Dilemmas
This section addresses the issues that arise when using absolute values of coefficients as probabilities, particularly the fact that the total probability condition leads to varying lengths of the quantum state depending on the observable being measured. The paragraph introduces a probability function 'f' that must satisfy two conditions: the sum of all probabilities must equal one, and the length of the quantum state must remain constant in any basis. It then explores the implications of these conditions, leading to the realization that most coefficients are independent of each other and that the last coefficient is constrained by the others. The paragraph sets the stage for finding the correct form of the probability function 'f'.
🧬 Deriving the Probability Function
The paragraph focuses on the mathematical derivation of the probability function 'f' that satisfies the conditions set forth in the previous section. It explains the process of using the conditions to find a differential equation for 'f' and how to solve for it. The paragraph highlights the importance of the independence of coefficients and the even nature of 'f', leading to the conclusion that the probability function must depend on the square of the coefficient. The constants of integration are determined, leading to the final form of the probability function, which relates the probability to the square of the coefficient divided by the square of the quantum state's length.
🌟 The Born Rule and Quantum Prescription
This paragraph wraps up the discussion by presenting the Born rule as the solution to the probability puzzle in quantum mechanics. It explains how the Born rule applies to both discrete and continuous eigenbases, and how it relates to the wavefunction. The paragraph also touches on the expectation value of an observable and how it can be calculated using the Born rule. Finally, it provides a comprehensive summary of the quantum prescription, which includes the representation of particles by quantum states in Hilbert space, the role of linear operators for observables, the process of quantum state collapse upon measurement, and the evolution of the quantum state after measurement.
Mindmap
Keywords
💡Quantum Mechanics
💡Eigenvectors and Eigenvalues
💡Born Rule
💡Quantum State
💡Linear Operators
💡Orthonormal Eigenbasis
💡Superposition
💡Probability Density
💡Wavefunction
💡Quantum Collapse
💡Expectation Value
Highlights
The Born rule is introduced, which is key to understanding the probability of particular outcomes in quantum mechanics.
Eigenvectors of an observable form an orthonormal eigenbasis, which is crucial for expanding quantum states.
Quantum states can be represented as a superposition of all possible values for an observable.
The probability of measuring a particular energy level is related to the component of the quantum state along the corresponding eigenvector.
The magnitude of the component along an eigenvector is initially thought to represent the probability of measuring that eigenvalue.
The sum of the absolute values of coefficients must equal one, representing the total probability of all possible outcomes.
The total length of a quantum state is not necessarily equal to one, leading to the need for rescaling depending on the observable.
The probability function must satisfy two conditions: the sum of probabilities for all outcomes equals one, and the length of the quantum state remains constant in any basis.
The probability function f is derived to depend on the square of the coefficient, leading to the Born rule.
The Born rule states that the measurement probability is equal to the amplitude squared of the coefficient of the eigenstate.
The concept of quantum state collapse is introduced, where the act of measurement collapses the state into a definite eigenstate.
The quantum prescription is a framework for quantum mechanics that includes a particle represented by a vector in Hilbert space and observables as linear operators.
The expectation value of an observable can be calculated using the eigenbasis expansion and the Born rule.
Gleason's theorem establishes the foundation of the Born rule for vector spaces of dimension 3 or greater.
The derivation of the Born rule and the quantum prescription provides an intuitive understanding of quantum mechanics' mathematical model.
Continuous eigenbases, like position, have a probability density function that is the squared magnitude of the coefficient in front of the eigenstate.
The wavefunction is the coefficient function in front of the eigenstate, which is related to probability density for continuous observables.
The act of measurement causes quantum state collapse into a random definite eigenstate, which is a mysterious and highly debated part of quantum mechanics.
Transcripts
Browse More Related Video

Ch 11: What are unitary operators? | Maths of Quantum Mechanics

Advanced Quantum Mechanics Lecture 1

Lecture 8 | Quantum Entanglements, Part 1 (Stanford)

Lecture 2 | Quantum Entanglements, Part 1 (Stanford)

Lecture 4 | The Theoretical Minimum
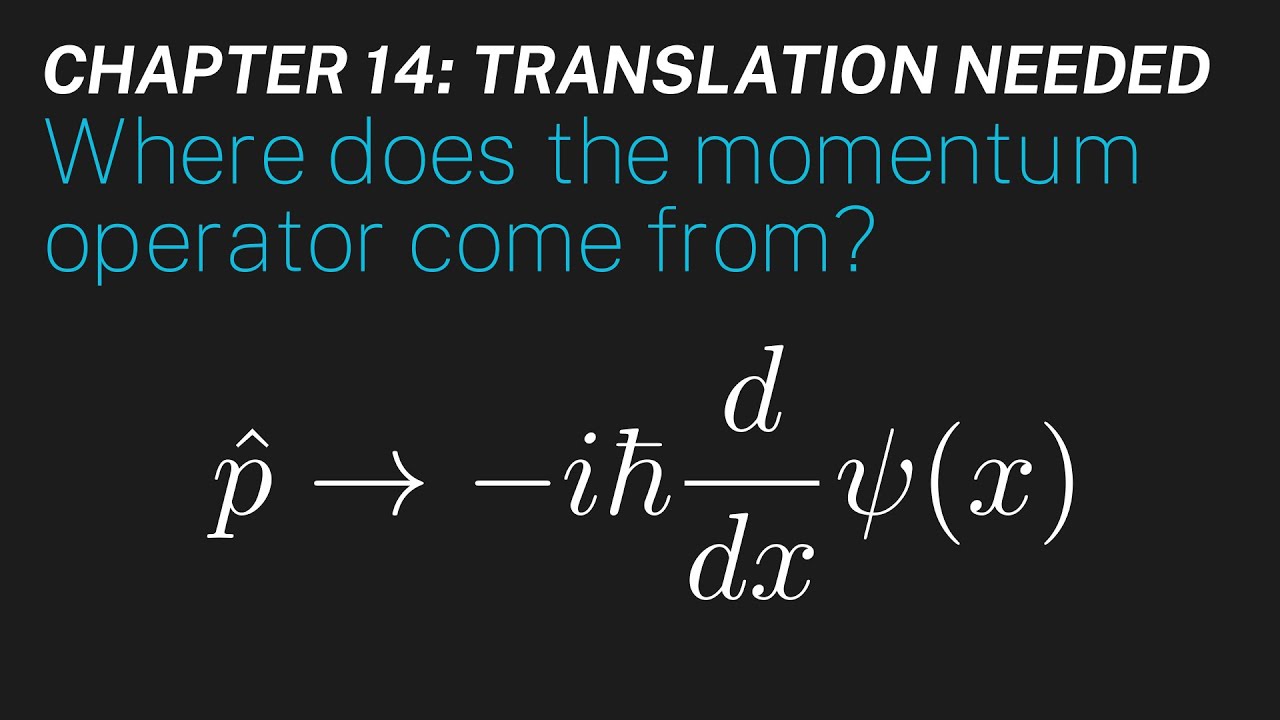
Ch 14: Where does the momentum operator come from? | Maths of Quantum Mechanics
5.0 / 5 (0 votes)
Thanks for rating: