Ch 14: Where does the momentum operator come from? | Maths of Quantum Mechanics
TLDRIn this episode, the focus is on the Schrödinger equation and the momentum operator's role in quantum mechanics. The video delves into the energy operator, Hamiltonian, and its relation to momentum. It explains how the translation operator works and its unitary nature, leading to the conclusion that spatial translations must conserve total probability. The script also explores the action of the momentum operator on a position wavefunction and derives the position-basis Schrödinger equation. The episode highlights the beauty of discovering patterns in physics and the importance of generators and symmetries in understanding quantum mechanics.
Takeaways
- 🌟 The Schrodinger equation depends on the energy operator, also known as the Hamiltonian, which is derived from the momentum squared divided by 2m plus the potential energy.
- 🔍 This episode focuses on understanding the momentum operator in quantum mechanics and its role as a derivative on the wavefunction.
- 📈 The translation operator is introduced, which shifts position eigenstates by a distance 'a' and is essential for analyzing the action of the momentum operator.
- 💡 Spatial translations are unitary, meaning they preserve the total probability of a quantum state, which is a crucial property derived from the inner product of the state with itself.
- 🌀 The generator of spatial change in classical physics is momentum, which is used to infer that the hermitian operator in the differential equation for the translation operator is the momentum operator.
- 🎭 The units of the equation are made consistent by introducing the reduced Planck constant, which is a fundamental constant in quantum mechanics.
- 📚 The momentum operator acts on a position wavefunction by taking its derivative and multiplying by -iħ (where ħ is the reduced Planck constant).
- 🌈 The position-basis Schrodinger equation is derived by projecting the Hamiltonian and the time evolution operator onto the position basis.
- 🔄 The Schrodinger equation can be represented in different bases (position, momentum, energy), each providing insights into how coefficients evolve in time.
- 🚀 The series concludes with this episode, but future topics such as the quantum path integral, Bell's theorem, and Bell inequalities are planned for future episodes.
Q & A
What is the Schrödinger equation dependent on?
-The Schrödinger equation is dependent on the energy operator, also known as the Hamiltonian.
How is the Hamiltonian represented in quantum mechanics?
-The Hamiltonian is represented as the momentum squared divided by 2m plus the potential energy.
What does the momentum operator do in quantum mechanics?
-The momentum operator acts as a derivative on the wavefunction, and it is involved in the Hamiltonian which is crucial in the Schrödinger equation.
What is the translation operator in quantum mechanics?
-The translation operator shifts a quantum state over by a distance 'a'. It acts on a position eigenstate to correspond to a new position eigenstate at 'x plus a'.
How does spatial translation affect the total probability of a quantum state?
-Spatial translations should conserve the total probability, as they only involve moving the quantum state without altering any other properties.
What is the significance of the unitary property in transformations in quantum mechanics?
-The unitary property ensures that transformations preserve the total probability, which is crucial for the conservation of probability in quantum mechanics.
How does the momentum operator act on a position wavefunction?
-The momentum operator acts by taking the derivative of the position wavefunction and multiplying by -i times the reduced Planck constant (ħ).
What is the relationship between the classical generator of motion and the quantum operators?
-In classical physics, the generator of motion (like momentum) is used to produce changes in position. Similarly, in quantum mechanics, the action of quantum operators (like the momentum operator) generates changes in quantum states.
How does the Schrödinger equation look in the position basis?
-In the position basis, the Schrödinger equation is represented as a partial differential equation involving the wavefunction, where the time-dependent Schrödinger equation is given by the kinetic energy term (minus i times ħ times the second derivative of the wavefunction with respect to position) plus the potential energy term (with the position operator replaced by the position variable).
What does the action of the momentum operator in the position basis represent?
-The action of the momentum operator in the position basis is represented as -i times ħ times the derivative of the wavefunction with respect to position, which is a fundamental aspect of quantum mechanics and is essential for understanding how quantum states evolve.
How can you derive the Schrödinger equation in different bases?
-By taking the inner product of the time-dependent Schrödinger equation with different basis states (position, momentum, or energy eigenstates), you can derive the Schrödinger equation in those respective bases, each providing insights into how the coefficients in those bases evolve over time.
Outlines
🌟 Quantum Mechanics: Schrodinger Equation and Momentum Operator
This paragraph introduces the focus on the Schrodinger equation and the momentum operator within quantum mechanics. It discusses the energy operator, also known as the Hamiltonian, which is central to the Schrodinger equation. The paragraph emphasizes the importance of understanding the momentum operator's role and its action as a derivative on the wavefunction. It also suggests reviewing previous content for a better grasp of the current material and sets the stage for a deep dive into the translation operator and its implications for total probability conservation and unitarity in quantum mechanics.
🔄 Understanding Spatial Translations and Unitarity
The second paragraph delves into the concept of spatial translations in quantum states and how they must be unitary operations to conserve total probability. It draws parallels with the time evolution operator from a previous episode, highlighting the mathematical similarities and the physical intuition behind unitarity. The paragraph also introduces the idea of using classical physics intuition to understand quantum mechanics, specifically the role of momentum as the generator of spatial change. It concludes with the derivation of an equation that relates the action of the momentum operator to the position wavefunction, emphasizing the beauty of the patterns found in physics.
📈 Deriving the Momentum Operator's Action on Position Wavefunctions
This paragraph focuses on the derivation of how the momentum operator affects position wavefunctions. It explains the process of acting the momentum operator on a quantum state and then expanding it in the position eigenbasis. The paragraph introduces the concept of integration by parts to move the derivative from the ket to the wavefunction, leading to a key equation that describes the momentum operator's action. It also clarifies the notation used for operator actions on wavefunctions and discusses the position-basis Schrodinger equation, providing a comprehensive understanding of its derivation and significance in quantum mechanics.
🌐 Exploring Different Basis Representations of the Schrodinger Equation
The final paragraph discusses various representations of the Schrodinger equation in different bases, such as momentum and energy eigenbases. It explains the process of projecting the Schrodinger equation into these bases and the resulting equations. The paragraph highlights the lesser-known momentum-basis Schrodinger equation and its utility, as well as the energy-basis equation, which is derived using a similar projection method. The summary emphasizes that all these equations represent the same fundamental physics, each describing how coefficients evolve in their respective bases over time. The paragraph concludes with a wrap-up of the series and a teaser for future episodes on quantum mechanics topics.
Mindmap
Keywords
💡Schrodinger Equation
💡Hamiltonian
💡Momentum Operator
💡Translation Operator
💡Unitary Operator
💡Energy Operator
💡Wavefunction
💡Quantum State
💡Position Eigenstate
💡Hermitian Operator
💡Reduced Planck Constant
Highlights
Derivation of the Schrödinger equation and its dependence on the energy operator, also known as the Hamiltonian.
Exploration of the momentum operator's role in quantum mechanics and its action as a derivative on the wavefunction.
Introduction to the translation operator and its effect on position eigenstates.
Explanation of how the translation operator acts on an arbitrary quantum state through position basis expansion.
Discussion on the conservation of total probability in spatial translations and the unitary nature of the translation operator.
Derivation of the equation for the translation operator and its relation to the time evolution operator.
Use of classical physics intuition to identify momentum as the generator of spatial change.
Establishment of the equation showing how the momentum operator acts on a position ket.
Connection between the units of inverse meters and momentum, necessitating the introduction of the reduced Planck constant.
Pattern identification in physics involving transformation operators, unitary transformations, and generators.
Derivation of the action of the momentum operator on the position wavefunction using integration by parts.
Clarification on the notation used when expressing the action of the momentum operator on wavefunctions.
Presentation of the position-basis Schrödinger equation and its derivation from the Hamiltonian.
Exploration of the Schrödinger equation in the momentum basis and its practical applications.
Introduction to the energy-basis Schrödinger equation and its significance in quantum mechanics.
Discussion on the importance of understanding different basis representations of the Schrödinger equation.
Preview of future topics to be covered, such as the quantum path integral, Bell's theorem, and Bell inequalities.
Conclusion of the series and appreciation for the viewers' engagement and interest in quantum mechanics.
Transcripts
Browse More Related Video

Advanced Quantum Mechanics Lecture 1

Advanced Quantum Mechanics Lecture 9

Lecture 9 | The Theoretical Minimum

Ch 12: What are generators in classical mechanics? | Maths of Quantum Mechanics

Lecture 4 | The Theoretical Minimum
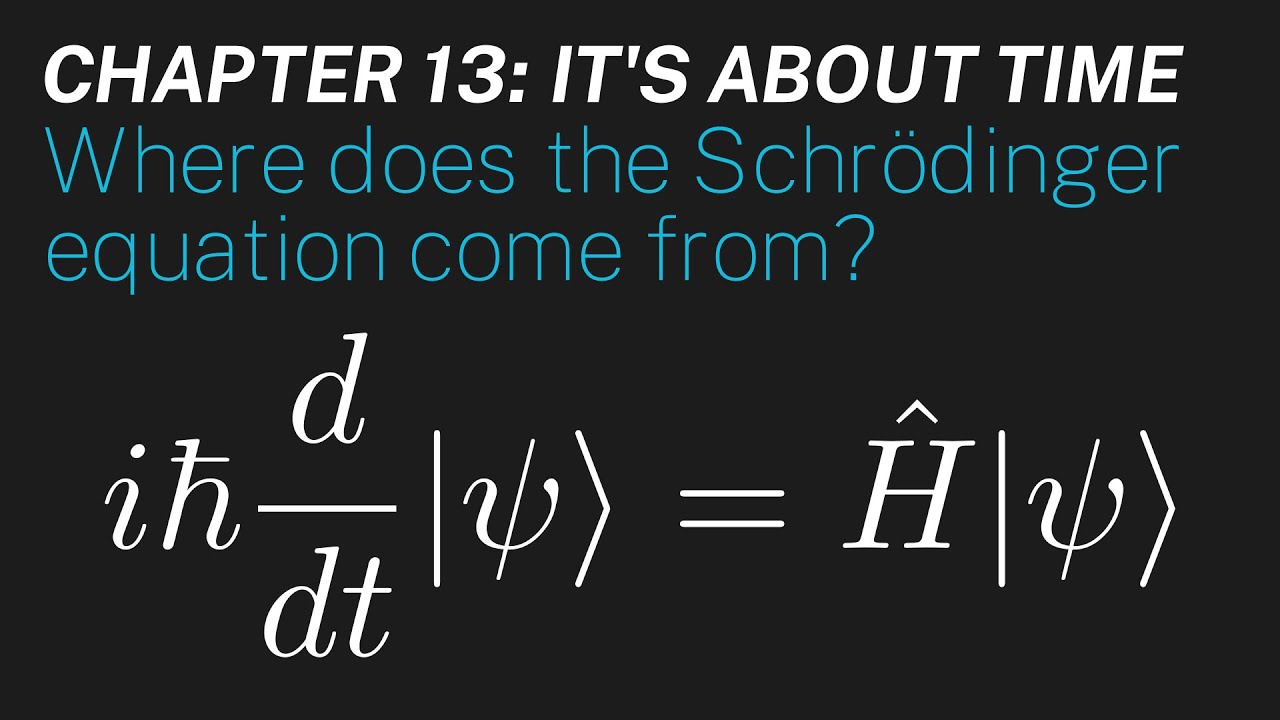
Ch 13: Where does the Schrödinger equation come from? | Maths of Quantum Mechanics
5.0 / 5 (0 votes)
Thanks for rating: