Ch 5: What are Dirac deltas and wavefunction inner products? | Maths of Quantum Mechanics

Quantum Sense
7 Jan 202310:30
EducationalLearning
32 Likes 10 Comments

TLDRThis episode delves into the concept of inner products in continuous linear combination scenarios, highlighting the role of the Dirac delta function. The Dirac delta is explained as a mathematical object that picks out specific values in integrals, often visualized as a 'big spike' at the origin with an integral of 1. The video clarifies that while this interpretation is intuitive, it's not rigorous, and discusses alternative limiting functions that also represent the Dirac delta. The episode concludes by connecting the Dirac delta to the orthonormal condition in quantum mechanics and its application in calculating the inner product of two vectors in a continuous basis.

Takeaways
  • 🌟 The episode focuses on inner products in the context of continuous linear combinations and introduces the Dirac delta function.
  • 🔍 To find a specific coefficient in a continuous basis expansion, the inner product is used in conjunction with the Dirac delta function.
  • 🎯 The Dirac delta function is defined by its integral property of picking out a specific value that makes its input equal to zero.
  • 🚫 The 'big spike' interpretation of the Dirac delta, while intuitive, is not rigorous and can lead to contradictions.
  • 📈 The Dirac delta can be represented by various limiting functions, not just the 'big spike', as long as they satisfy the integral property.
  • 🌐 The Fourier transform and its inverse involve a form of the Dirac delta that does not fit the 'big spike' interpretation.
  • 💡 The mathematical definition of the Dirac delta is based on its integral property, without specifying its shape.
  • 🌟 The orthonormal condition in continuous spaces involves the Dirac delta instead of the Kronecker delta, maintaining the intuitive understanding of when inner products are non-zero.
  • 📚 The inner product of two vectors in a continuous basis is shown to be similar to the discrete case, with the Dirac delta replacing the Kronecker delta.
  • 📈 The process of taking the inner product involves expanding the vectors, moving inner products, and using the Dirac delta's property to simplify the integral.
  • 🔄 The episode concludes by emphasizing the importance of the inner product as a versatile tool in quantum theory and previews the next topic on bra-ket notation.
Q & A

  • What is the main topic of discussion in this episode?

    -The main topic of discussion in this episode is the concept of inner products in the context of continuous linear combinations and how it leads to the Dirac delta function.

  • What is a continuous orthonormal basis?

    -A continuous orthonormal basis is a set of functions that are orthogonal and normalized over a continuous domain, allowing for the expansion of any vector in that space.

  • How does the Dirac delta function help in extracting a specific coefficient from a continuous orthonormal expansion?

    -The Dirac delta function helps in extracting a specific coefficient by integrating against it, which picks out the particular value that makes its input equal to zero, effectively isolating the desired coefficient.

  • What is the 'big spike' interpretation of the Dirac delta?

    -The 'big spike' interpretation of the Dirac delta is the idea that it is a function that is equal to infinity at the origin and zero everywhere else, with an integral equal to 1.

  • What are some limitations of the 'big spike' interpretation of the Dirac delta?

    -The 'big spike' interpretation is not rigorous because it is not mathematically consistent to have a function that is equal to infinity at a point while having an integral of one. Additionally, it does not hold true for all functions that can act as Dirac deltas, such as those that oscillate indefinitely away from the central point.

  • How can the Dirac delta be understood mathematically?

    -Mathematically, the Dirac delta is understood as a distribution that satisfies the property of picking out the value that makes its input equal to zero when integrated against a well-behaved function.

  • What is the role of the Dirac delta in the orthonormal condition for continuous orthonormal bases?

    -In the orthonormal condition for continuous orthonormal bases, the Kronecker delta is replaced by the Dirac delta, which is zero when the functions are not the same and non-zero (equal to one) when they are the same.

  • How does the inner product of two vectors in a continuous orthonormal basis compare to the discrete case?

    -The inner product of two vectors in a continuous orthonormal basis is similar to the discrete case, but instead of a sum (double sum in the discrete case), it is represented as a double integral, and the Kronecker delta is replaced by the Dirac delta.

  • What is the significance of the inner product in quantum mechanics?

    -The inner product is significant in quantum mechanics as it is one of the most versatile tools within the theory, allowing for the calculation of probabilities and the understanding of the relationship between quantum states.

  • What is the next topic that will be introduced in the series?

    -The next topic in the series will be the introduction of the 'bra' and an explanation of the origin of bra-ket notation in quantum mechanics.

  • How does the speaker suggest we should understand and use the Dirac delta?

    -The speaker suggests that while the 'big spike' interpretation is useful for intuitive understanding, we should not use it as a strict definition due to its limitations. Instead, we should focus on the mathematical property that defines the Dirac delta and use it as a tool that satisfies this property.

Outlines
00:00
🌟 Introduction to Continuous Inner Products and Dirac Delta

This paragraph introduces the concept of inner products in the context of continuous linear combinations, highlighting the transition from discrete to continuous cases. It emphasizes the role of the Dirac delta function in extracting specific coefficients from a continuous orthonormal basis expansion. The Dirac delta is described as a function that picks out a particular value from a function by integrating against it. The explanation delves into the 'big spike' interpretation of the Dirac delta, which is intuitive but not rigorous, and sets the stage for a deeper exploration of the Dirac delta's properties and its significance in quantum mechanics.

05:00
🔍 Dissecting the Dirac Delta: Beyond the 'Big Spike' Interpretation

The paragraph delves deeper into the Dirac delta, questioning the 'big spike' interpretation and exploring alternative limiting functions that also satisfy the integral property of the Dirac delta. It presents an example of a function that behaves like a Dirac delta in the context of Fourier transforms, which does not fit the 'big spike' model but is still valid. The speaker advises against using the 'big spike' interpretation as a strict definition due to its limitations, and instead offers a mathematical understanding of the Dirac delta based on its integral property. This understanding is crucial for physicists and provides a balance between intuition and mathematical consistency.

10:02
📚 Quantum Mechanics and the Inner Product Revisited

The final paragraph brings the discussion back to quantum mechanics, focusing on the修正 of the orthonormal condition to include the Dirac delta for continuous inner products. It reiterates the process of taking the inner product of two vectors expanded in a continuous orthonormal basis, leading to the familiar 'inner product for wavefunctions.' The speaker emphasizes the versatility of the inner product as a fundamental tool in quantum theory and provides a preview of upcoming topics, including the introduction of bra and bra-ket notation, encouraging viewers to engage with the material and look forward to future episodes.

Mindmap
Keywords
💡Inner Product
The inner product is a mathematical operation that takes two vectors and produces a scalar. In the context of the video, it is used to extract coefficients from a vector in both discrete and continuous linear combination cases. The inner product is shown to be a fundamental tool in quantum mechanics, allowing for the calculation of the relationship between different vectors in a space.
💡Discrete Linear Combination
A discrete linear combination is a sum of discrete elements, each multiplied by its own coefficient, to form a new vector or function. The video compares the use of inner products in discrete linear combinations to their use in continuous ones, highlighting the transition from discrete to continuous mathematical concepts.
💡Continuous Linear Combination
A continuous linear combination extends the concept of a linear combination to include an infinite or continuous number of elements. In the video, this concept is used to explain how inner products can be applied in scenarios involving functions that vary continuously over a range.
💡Dirac Delta
The Dirac delta is a theoretical function used in physics and engineering, often visualized as a 'big spike' at the origin with an area under the curve equal to one. It is used to pick out specific values in integrals, such as the coefficient for a particular value of x in a continuous orthonormal basis.
💡Orthonormal Basis
An orthonormal basis is a set of vectors that are orthogonal (perpendicular) and normalized (of unit length). In the context of the video, a continuous orthonormal basis allows for the expansion of any vector in a space, which is crucial for understanding the behavior of inner products in quantum mechanics.
💡Right-Linearity
Right-linearity is a property of the inner product where the inner product of a scalar multiple of a vector with another vector is equal to the scalar multiple of the inner product of the two vectors. This property is used in the video to move the inner product inside an integral, which is essential for extracting coefficients in continuous linear combinations.
💡Big Spike Interpretation
The 'big spike' interpretation of the Dirac delta is a visual and intuitive way to understand its behavior, where it is thought of as being infinite at a certain point (the origin) and zero everywhere else. While useful for intuitive understanding, this interpretation is not rigorous and does not hold up under mathematical scrutiny.
💡Fourier Transform
The Fourier transform is a mathematical technique used to decompose a function or a signal into its constituent frequencies. The Dirac delta function plays a significant role in Fourier transforms, as it can be obtained as a limit of certain functions under specific conditions.
💡Quantum Mechanics
Quantum mechanics is a fundamental theory in physics that describes the behavior of matter and energy at very small scales, such as atomic and subatomic particles. The Dirac delta function and inner products are essential mathematical tools in quantum mechanics for dealing with wavefunctions and their properties.
💡Bra-Ket Notation
Bra-ket notation is a convenient way of writing quantum states and their inner products in quantum mechanics. The 'bra' represents the complex conjugate of a state vector, and the 'ket' represents the state vector itself. This notation is used to describe the probability amplitudes of quantum states.
💡Kronecker Delta
The Kronecker delta is a mathematical function that takes on the value 1 when its two arguments are equal and 0 when they are not. It is used in the context of discrete linear combinations and is replaced by the Dirac delta in the continuous case.
Highlights

Introduction to inner products in the context of continuous linear combinations.

Explanation of how to use inner products to extract coefficients from a vector.

Discussion on the use of the Dirac delta in the context of inner products.

The Dirac delta's ability to pick out specific values from a function through integration.

Clarification on the 'big spike' interpretation of the Dirac delta.

The integral property of the Dirac delta and its physical interpretation.

Limiting functions that act as a Dirac delta and their implications.

The mathematical understanding of the Dirac delta beyond the 'big spike' interpretation.

The definition of the Dirac delta based on its integral property.

The modification of the orthonormal condition in continuous orthonormal inner products.

The process of taking the inner product of two vectors expanded in a continuous orthonormal basis.

The inner product of orthonormal states expressed as a Dirac delta.

The role of the Dirac delta in simplifying the inner product of wavefunctions.

The importance of the inner product as a versatile tool in quantum theory.

Preview of the next episode's content: introduction to the bra and the origin of bra-ket notation.

Encouragement for viewers to engage with the material and ask questions.

Transcripts

Browse More Related Video

Ch 4: What is an inner product? | Maths of Quantum Mechanics

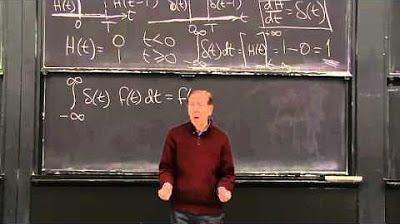
Step Function and Delta Function

Lecture 4 | New Revolutions in Particle Physics: Basic Concepts

Calculus 1: The Epsilon-Delta Definition of the Limit

6.2 Entropy, Gibbs Free Energy, and the Equilibrium Constant | Organic Chemistry

Ch 2: What are kets and wavefunctions? | Maths of Quantum Mechanics

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
QuantumMechanicsInnerProductsDiracDeltaContinuousBasisMathematicalToolsPhysicsConceptsEducationalContentLinearAlgebraOrthonormalBasisQuantumTheory