Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (50 of 92) What is Oscillator Amplitude?

Michel van Biezen
8 Apr 201805:04
EducationalLearning
32 Likes 10 Comments

TLDRThe lecture discusses the oscillation amplitude of diatomic molecules, using carbon monoxide as a case study. It explains how the amplitude varies with quantum energy levels and compares it to the equilibrium bond length. The lecture covers the calculation of vibrational frequency, zero-point energy, and energy transitions between quantum states. It also illustrates how the amplitude increases with energy levels, providing specific percentages relative to the bond length at different quantum states.

Takeaways
  • πŸ“Œ The lecture focuses on analyzing the oscillation amplitude of diatomic molecules, specifically carbon monoxide (CO).
  • πŸ” The equilibrium bond length between carbon and oxygen in CO is 112.8 picometers or 0.113 nanometers.
  • πŸ’« Even at absolute zero (0 Kelvin), molecules vibrate due to quantum mechanical energy, with an amplitude of 1/2 Hbar Omega.
  • πŸ“ˆ The frequency of oscillation can be calculated using the formula √(K/m), resulting in 4.1 x 10^14 oscillations per second for CO.
  • ⚑ The zero-point energy is approximately 4 x 10^-20 Joules, which corresponds to 0.135 electron volts.
  • 🌐 Energy transitions between quantum states result in amplitude changes, doubling the energy results in a doubled amplitude.
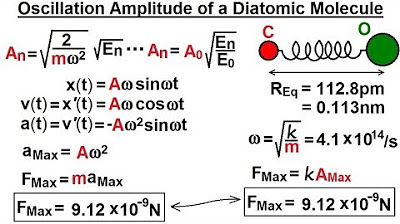
  • πŸ“Š The amplitude at any quantum level can be calculated using the formula √(2/K) * (MΞ©)^2 * √(n), where n is the quantum number.
  • πŸ”Ž The amplitude ratio at different energy levels compared to the zero energy level is the square root of the energy level ratio.
  • πŸ”’ At quantum levels 0, 1, 2, and 10, the energy and amplitude increase, with amplitudes being 0.42%, 7.3%, 9.4%, and 19.2% of the total bond distance, respectively.
  • πŸ€” The reduced mass used in calculations is the product of the masses of carbon and oxygen atoms divided by their sum, providing an equivalent mass for the oscillator model.
Q & A

  • What is the main topic of the lecture?

    -The main topic of the lecture is to determine and understand the oscillation amplitude of a diatomic molecule, specifically carbon monoxide (CO), at various quantum energy levels and to compare it with the typical bond length between the two atoms.

  • What is the equilibrium bond length of the carbon monoxide molecule?

    -The equilibrium bond length of the carbon monoxide molecule is 112.8 picometers, which is equivalent to 0.113 nanometers.

  • How does the molecule's vibration change at absolute zero Kelvin?

    -Even at absolute zero Kelvin, the molecule will still vibrate with the quantum mechanical energy it possesses, which is 1/2 Hbar Omega.

  • What is the frequency of oscillation for the carbon monoxide molecule?

    -The frequency of oscillation for the carbon monoxide molecule is the square root of (K/m), which is approximately 4.1 times 10^14 oscillations per second.

  • How is the energy at the zero energy level calculated?

    -The energy at the zero energy level (E_sub_nought) is calculated to be about 4 times 10^-20 joules, which is equivalent to 0.135 electron volts when converted.

  • What is the formula to calculate the amplitude at any quantum level?

    -The amplitude at any quantum level (n) can be calculated using the formula: amplitude = sqrt(2/K) * M * Omega^2 * sqrt(E_n), where E_n is the energy at that quantum level.

  • How does the amplitude change as the quantum energy level increases?

    -As the quantum energy level increases, the amplitude increases proportionally to the square root of the energy level. For example, at the first quantum level (N=1), the amplitude increases by the square root of 3, and at the fifth quantum level (N=5), the amplitude is 2.5 times that of the first level.

  • What is the percentage of the amplitude relative to the bond length at the zero energy level?

    -At the zero energy level, the amplitude is 4.7 picometers, which is 4.2% of the total bond length between the two atoms.

  • How does the reduced mass affect the oscillator model?

    -The reduced mass, which is the product of the masses of the carbon and oxygen atoms divided by the sum of the two, is used in the oscillator model to determine the equivalent mass that influences the oscillation properties of the carbon monoxide molecule.

  • What is the significance of understanding the oscillation amplitude at different quantum states?

    -Understanding the oscillation amplitude at different quantum states provides a realistic picture of molecular vibrations and helps in predicting the behavior of molecules under various energy conditions, which is crucial for studying chemical bonding and molecular properties.

Outlines
00:00
πŸ“š Introduction to Diatomic Molecule Oscillation

This paragraph introduces the topic of diatomic molecule oscillation, focusing on the carbon monoxide (CO) molecule. It discusses the aim to determine the oscillation amplitude at various quantum energy levels and compares these to the typical bond length of the molecule. The equilibrium bond length of CO is given as 112.8 picometers or 1.13 nanometers. The paragraph sets the stage for exploring how the molecule's oscillation amplitude changes as it gains energy, even at absolute zero temperature, where it still vibrates with quantum mechanical energy.

Mindmap
Keywords
πŸ’‘Diatomic molecule
A diatomic molecule is a type of chemical compound that consists of two atoms of the same or different elements bonded together. In the context of the video, carbon monoxide (CO) is used as an example of a diatomic molecule, where one carbon atom is bonded to one oxygen atom.
πŸ’‘Oscillation amplitude
The oscillation amplitude refers to the maximum displacement of a particle from its equilibrium position during a vibrational cycle. In the video, the amplitude is used to describe the extent of vibration of the diatomic molecule at different energy levels, with the amplitude increasing as the molecule gains energy.
πŸ’‘Quantum energy levels
Quantum energy levels are the specific, discrete energy states that a quantum system can occupy. In the case of a diatomic molecule, these levels are associated with the vibrational energy of the molecule. The video explains how the energy levels and the corresponding amplitude of oscillation change as the molecule transitions between these states.
πŸ’‘Bond length
The bond length is the distance between the nuclei of two bonded atoms. It is a critical parameter in understanding the geometry and properties of a molecule. In the video, the equilibrium bond length of carbon monoxide is given as 112.8 picometers or 0.113 nanometers.
πŸ’‘Equilibrium position
The equilibrium position is the stable, lowest-energy configuration of a system where the forces are balanced. For a diatomic molecule, this is the ideal bond length at which the attractive and repulsive forces between the atoms are in equilibrium. The video uses the equilibrium position as a reference point to discuss molecular vibrations.
πŸ’‘Zero-point energy
Zero-point energy is the lowest possible energy that a quantum mechanical system can have, which is greater than absolute zero. Even at absolute zero temperature, particles in a system still possess this residual energy, leading to vibrations in molecules. The video explains that the zero-point energy is present in the carbon monoxide molecule at the zero energy level.
πŸ’‘Frequency
Frequency refers to the number of occurrences of a repeating event per unit of time. In the context of molecular vibrations, it is the number of oscillations a molecule makes per second. The video calculates the frequency of the carbon monoxide molecule's vibration using the formula square root of (K/m), resulting in 4.1 x 10^14 oscillations per second.
πŸ’‘Reduced mass
The reduced mass is a concept used in the description of a two-particle system, such as a diatomic molecule, where it is the product of the two masses divided by the sum of the two masses. It simplifies the analysis of the system by treating it as a single particle with this effective mass. The video mentions the use of the reduced mass in calculating the oscillations of the carbon monoxide molecule.
πŸ’‘Energy quantization
Energy quantization is the concept that certain physical quantities, such as energy, can only take on discrete values rather than a continuous range. In the context of molecular vibrations, this means that a molecule can only occupy specific energy levels rather than any arbitrary energy value. The video discusses how the energy jumps from one quantized level to another.
πŸ’‘Amplitude ratio
The amplitude ratio is the comparative measure of the oscillation amplitudes at different quantum energy levels relative to the amplitude at the zero energy level. It provides insight into how the vibrational displacement of a molecule changes with energy. The video calculates this ratio using the square root of the energy level ratio.
Highlights

The lecture focuses on diatomic molecules and their oscillation amplitude at various quantum energy levels.

Carbon monoxide (CO) molecule is used as an example, consisting of one carbon and one oxygen atom.

The equilibrium bond length for CO is 112.8 picometers or 0.113 nanometers.

Even at absolute zero (0 Kelvin), molecules still vibrate due to quantum mechanical energy.

The frequency of oscillation for CO can be calculated using the formula √(K/m), resulting in 4.1 x 10^14 oscillations per second.

The zero energy level (E_sub_0) has an amplitude of 4.7 picometers, which is 4.2% of the total bond distance.

The amplitude increases with the quantum energy level; for n=1, the amplitude is about 8.2 picometers (7.3% of the bond distance).

At the fifth quantum level (n=5), the amplitude is approximately 9.4% of the total bond distance.

At the tenth quantum level (n=10), the amplitude reaches 21.7 picometers, which is 19.2% of the total bond distance.

The reduced mass used in calculations is the product of the carbon and oxygen atom masses divided by their sum.

The lecture provides a realistic scenario for understanding the oscillation amplitude of a real molecule like CO.

The oscillation amplitude is directly related to the quantum energy level of the molecule.

The energy jumps between quantum states are quantified in electron volts, with the zero energy level having 0.135 eV.

The energy at higher quantum levels can be calculated using the ratio of energy levels and amplitudes.

The lecture demonstrates the physical feel of oscillation amplitude in relation to the bond distance of diatomic molecules.

The theoretical contributions include the use of quantum mechanics to understand molecular vibrations.

Practical applications may involve using these insights to predict molecular behavior under different energy conditions.

Transcripts

Browse More Related Video

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (48 of 92) How Oscillator Increases energy

5. Resonance V and Atoms I

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (39 of 92) What is the Quantum Oscillator?

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (51 of 92) Oscillator Amplitude - Diatomic

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (42 of 92) k=? of a Diatomic Molecule

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (46 of 92) Quantum Nature of Oscillator 2

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Quantum MechanicsDiatomic MoleculesOscillation AmplitudeBond LengthCarbon MonoxideEnergy StatesVibrational AnalysisMolecular PhysicsReduced MassScientific Lecture