Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (31 of 92) Momentum Eigenfunction Particle

Michel van Biezen
1 Dec 201707:46
EducationalLearning
32 Likes 10 Comments

TLDRThis video script delves into the quantum mechanics concept of finding the momentum eigenfunctions for a particle within a one-dimensional box. The presenter begins by revisiting the previously determined eigenvalues and then explains the process of applying the momentum operator to the presumed eigenfunctions. Through a series of mathematical manipulations involving sine and cosine functions, and the use of Euler's formula, the script demonstrates how the momentum eigenfunctions are derived. The key insight is that the eigenfunctions must satisfy the momentum operator equation, leading to the conclusion that the functions in exponential form, with specific constants, are indeed the correct momentum eigenfunctions for the system.

Takeaways
  • 📌 The video's objective is to find the momentum eigenfunctions of a particle in a one-dimensional box, building upon the eigenvalues found in a previous video.
  • 🔍 The process starts by applying the momentum operator on the presumed eigenfunction, aiming to prove the relationship between the momentum eigenvalue and the eigenfunction.
  • 🌟 The momentum eigenvalue is given by nπħ/L, where n is an integer, ħ is the reduced Planck constant, and L is the length of the box.
  • 🚫 A crucial realization is that the eigenfunction must be a sine function, not a cosine, to satisfy the momentum operator equation, as the derivative of a sine function is a cosine with the same argument.
  • 📈 The video demonstrates the transformation of sine functions into exponential form, which allows for the correct application of the momentum operator.
  • 🧠 The concept of taking the derivative of an exponential function is used to derive the product of the eigenvalue and eigenfunction.
  • 🔄 The process is shown for both positive and negative eigenfunctions, confirming the validity of the momentum eigenfunctions in both directions.
  • 🌐 The video emphasizes the importance of constants in the exponential form to ensure that the derivative yields the correct eigenvalue-eigenfunction product.
  • 🔢 The eigenvalue for negative momentum is shown to be -nπħ/L, reflecting the directionality of momentum.
  • 🎓 The video concludes by confirming that the derived functions are indeed the momentum eigenfunctions for a particle in a one-dimensional box.
  • 💡 The lesson highlights the mathematical rigor required to validate the eigenfunctions and eigenvalues in quantum mechanics problems.
Q & A

  • What is the main goal of the video?

    -The main goal of the video is to find the momentum eigenfunctions of a particle in a one-dimensional box.

  • What is the relationship between the momentum operator and the presumed eigenfunction?

    -The relationship is such that when the momentum operator is applied to the presumed eigenfunction, it should equal the momentum eigenvalue times the momentum eigenfunction.

  • What is the momentum eigenvalue for a particle in a one-dimensional box?

    -The momentum eigenvalue is given by nπħ/L, where n is an integer.

  • Why does the video switch from operating on the momentum eigenfunction to the energy eigenfunction?

    -The switch is made to demonstrate that the eigenfunctions of momentum and energy are distinct, as operating on the energy eigenfunction does not yield the same result as operating on the momentum eigenfunction.

  • How does the video justify the use of sine and cosine functions for the eigenfunctions?

    -The video justifies the use of sine and cosine functions by showing that when the momentum operator is applied to these functions, the result does not match the expected eigenvalue times eigenfunction, indicating that sine and cosine functions cannot be the eigenfunctions of the momentum operator.

  • What is the significance of expressing the eigenfunctions in exponential form?

    -Expressing the eigenfunctions in exponential form allows for the application of the momentum operator to yield the correct eigenvalue times eigenfunction, as the derivative of an exponential function is the same exponential function times the derivative of the exponent.

  • How does the video derive the momentum eigenfunctions for a positive momentum?

    -The video derives the positive momentum eigenfunctions by applying the momentum operator to an exponential function, taking the derivative, and then adjusting the constants so that the result matches the expected eigenvalue times eigenfunction.

  • What is the process for finding the momentum eigenfunctions for a negative momentum?

    -The process for negative momentum is similar to that for positive momentum, but with the negative exponential function and the negative sign in the eigenvalue, resulting in the correct eigenfunction for negative momentum.

  • How does the video confirm that the derived functions are indeed the momentum eigenfunctions?

    -The video confirms this by showing that when the derived functions are operated on by the momentum operator, the result matches the expected eigenvalue times eigenfunction, both for positive and negative momentum.

  • What is the role of the constants in front of the exponential functions in the eigenfunctions?

    -The constants are crucial for ensuring that when the momentum operator is applied, the derivative results in the correct eigenvalue times eigenfunction, thus validating the functions as the correct momentum eigenfunctions.

  • What is the conclusion of the video regarding the momentum eigenfunctions of a particle in a one-dimensional box?

    -The conclusion is that the derived exponential functions, with appropriate constants, are indeed the momentum eigenfunctions for both positive and negative momentum values in a one-dimensional box.

Outlines
00:00
📚 Introduction to Momentum Eigenfunctions

This paragraph introduces the concept of finding the momentum eigenfunctions for a particle within a one-dimensional box. It explains the process of operating the momentum operator on a presumed eigenfunction and equating it to the momentum eigenvalue times the eigenfunction. The discussion includes a review of the previous video's findings on eigenvalues and sets the stage for the exploration of eigenfunctions in the context of momentum. The paragraph also highlights the importance of validating the eigenfunctions by operating on them with the momentum operator and explains the mathematical process involved in deriving the momentum eigenfunctions.

05:01
🔍 Derivation of Momentum Eigenfunctions

The second paragraph delves into the derivation of the momentum eigenfunctions by operating on the energy eigenfunction instead of the momentum eigenfunction. It outlines the mathematical steps and reasoning behind choosing specific functions that, when differentiated, yield the product of the eigenvalue and eigenfunction. The paragraph explains the transformation of sine functions into exponential form and how this facilitates the correct derivation of the momentum eigenfunctions. It also discusses the process of taking derivatives of exponential functions and how it leads to the identification of the eigenvalues for both positive and negative momentum states of the particle in the one-dimensional box.

Mindmap
Keywords
💡momentum
In the context of the video, momentum refers to the quantity of motion of a particle, which is being explored in relation to a one-dimensional box model. Momentum is a fundamental concept in physics, defined as the product of an object's mass and velocity. In quantum mechanics, as discussed in the video, momentum is represented by an operator and has discrete eigenvalues for a particle in a one-dimensional box, given by nπħ/L, where n is an integer, ħ is the reduced Planck constant, and L is the length of the box. The video aims to find the eigenfunctions associated with these momentum eigenvalues.
💡eigenfunctions
Eigenfunctions are specific functions that, when used in certain mathematical operations, result in a scalar multiple of themselves. In the video, the host is trying to find the momentum eigenfunctions, which are the functions that correspond to the momentum eigenvalues of a particle in a one-dimensional box. These eigenfunctions are crucial for solving quantum mechanical problems and providing a complete description of the quantum states within the box.
💡one-dimensional box
A one-dimensional box, in quantum mechanics, is a thought experiment that involves a particle confined to move within a straight line of length L. This model is used to illustrate and understand the quantization of energy and momentum in quantum systems. The video is focused on finding the momentum eigenfunctions for such a system, which helps in understanding the behavior of particles under these constraints.
💡quantum mechanics
Quantum mechanics is a fundamental theory in physics that describes the behavior of matter and energy at very small scales, such as atomic and subatomic particles. The video's discussion of momentum eigenvalues and eigenfunctions is rooted in quantum mechanics, as it explores the quantized nature of these properties within a one-dimensional box model.
💡operator
In mathematics and physics, an operator is a symbol or function that acts on a variable or function to produce another function. In quantum mechanics, operators are used to represent physical quantities like momentum and energy. The video discusses the momentum operator and its action on eigenfunctions to find the momentum eigenfunctions.
💡eigenvalue
An eigenvalue is a scalar that, when a linear operator is applied to an eigenvector, the result is the eigenvalue times the eigenvector. In the context of the video, the eigenvalues of the momentum operator for a particle in a one-dimensional box are quantized and given by nπħ/L, where n is an integer. These eigenvalues are crucial for understanding the allowed momentum states within the box.
💡sine function
A sine function is a trigonometric function that oscillates between -1 and 1 and is commonly used in wave-like patterns. In the video, sine functions are used to describe the energy eigenfunctions of the particle in the one-dimensional box. These functions are essential for constructing the momentum eigenfunctions, as they satisfy the boundary conditions of the system.
💡cosine function
A cosine function, like the sine function, is a trigonometric function that describes periodic phenomena. It is used in the video to contrast with the sine function when discussing the action of the momentum operator on the energy eigenfunction. The cosine function is not equal to the eigenvalue times the momentum eigenfunction, which is why sine functions are used instead.
💡exponential form
The exponential form refers to expressing functions in terms of exponentials, which is a common technique in mathematics and physics. In the video, the sine function is expressed in its exponential form, e^(iθ) - e^(-iθ) / 2i, to facilitate the derivation of the momentum eigenfunctions. This form allows for the use of calculus operations, such as differentiation, which is crucial in the process of finding the eigenfunctions.
💡derivative
The derivative is a mathematical operation that finds the rate of change or the slope of a function. In the context of the video, derivatives are used to transform the exponential form of the sine function into the momentum eigenfunctions. The process involves taking the derivative of the exponential form to obtain the function that satisfies the momentum eigenvalue equation.
💡boundary conditions
Boundary conditions are constraints that must be satisfied at the edges of a system or domain. In the one-dimensional box model, the boundary conditions require that the wave functions (eigenfunctions) are zero at the walls of the box. These conditions are essential for determining the allowed energy and momentum states of the particle within the box.
Highlights

The video aims to find the momentum eigenfunctions of a particle in a one-dimensional box.

The momentum operator is applied to the presumed eigenfunction to yield the momentum eigenvalue times the eigenfunction.

The momentum eigenvalue is given by n PI H bar over L, derived from previous knowledge.

To validate the eigenfunctions, the momentum operator is operated on the energy eigenfunction, leading to a different result than the momentum eigenfunction.

The sine function, which is the eigenfunction, is contrasted with the cosine function obtained from the momentum operator application.

The concept of expressing sine in exponential form is introduced to find the correct eigenfunctions.

The process of taking the derivative of the exponential form is expected to yield the product of the eigenvalue and eigenfunction.

The positive eigenfunction is operated on by the momentum operator to derive the momentum eigenvalue.

The derivative of the exponential function results in the same exponential function times the derivative of the exponent.

The eigenvalue of the momentum of a particle is identified in the process of derivation.

Constants are adjusted to ensure the derivative yields the correct eigenvalue times eigenfunction.

The negative eigenfunction is also operated on by the momentum operator to find its corresponding eigenvalue.

The negative eigenvalue results in a minus n PI H bar over L, reflecting the direction of momentum.

The process confirms that the chosen eigenfunctions work for both positive and negative momentum directions.

The final result confirms that the identified functions are indeed the momentum eigenfunctions of a particle in a one-dimensional box.

The video provides a detailed explanation of how the momentum eigenfunctions are derived and validated.

The use of exponential form for sine functions is a key step in the derivation process.

The video demonstrates the application of quantum mechanics principles to solve for eigenfunctions in a specific scenario.

Transcripts

Browse More Related Video

Lecture 5: Operators and the Schrödinger Equation

Lecture 16: Eigenstates of the Angular Momentum Part 2

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (30 of 92) Momentum Eigenvalue=? n=1

Lecture 15: Eigenstates of the Angular Momentum Part 1

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (29 of 92) Expect. Value Momentum=? 1-D Box

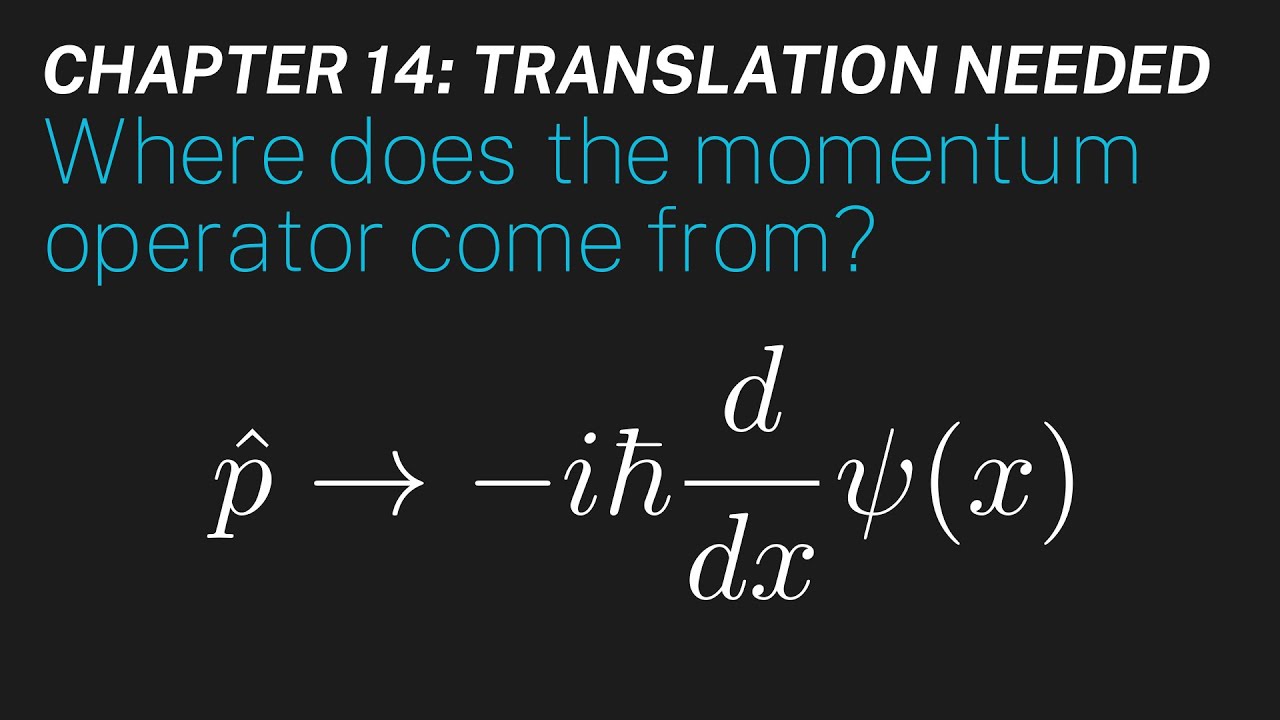
Ch 14: Where does the momentum operator come from? | Maths of Quantum Mechanics

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
QuantumMechanicsMomentumEigenfunctions1DBoxMathDerivationsWaveFunctionsEigenvaluesPhysicsEducationQuantumTheorySchrodingerEquationWave-ParticleDuality