Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (25 of 92) Prob. of a Particle 1-D Box n=1

Michel van Biezen
25 Nov 201708:18
EducationalLearning
32 Likes 10 Comments

TLDRThis video delves into the probability of locating a particle within a specific section of a one-dimensional box, depending on its energy state. The ground state probability density function resembles a sine or cosine wave, with the highest likelihood in the box's center. In contrast, for the first excited state (N=2), the probability at the box's midpoint is zero. The video illustrates this by calculating the probability density function for the ground state and shows that the particle's probability distribution changes significantly with its energy level, affecting the likelihood of finding it in a particular box region.

Takeaways
  • 🌟 The probability of finding a particle in a one-dimensional box depends on its energy state, with different patterns for ground state and excited states.
  • 📈 In the ground state (N=1), the probability density function resembles a sine or cosine wave, with the highest probability in the middle of the box.
  • 📊 For the first excited state (N=2), the probability density function changes significantly, with the probability at the box's center being zero.
  • 🧪 The video demonstrates the calculation of the probability density function for the ground state using the Schrödinger equation and integrating over a specific range within the box.
  • 🔢 By integrating the probability density function from 0.45L to 0.55L, the video shows that there's a 19.8% chance of finding the particle in that range, despite it being only 10% of the box's length.
  • 🌐 The probability distribution is not uniform across the box, with certain regions having a higher likelihood of finding the particle based on its energy state.
  • 🎥 The video script includes a step-by-step mathematical breakdown of the integrals involved in calculating the probability.
  • 📚 The use of trigonometric identities and proper differentials is crucial for accurate integration and probability calculation.
  • 🔄 The process of splitting the integral into separate parts and evaluating them individually is highlighted to simplify the calculation.
  • 📈 The results indicate that the particle is more likely to be found in certain areas of the box, which aligns with the wave-like nature of the probability density function.
  • 🚀 The video sets up for a follow-up exploration in the next episode, where the probability for the particle in the second energy level will be examined.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is exploring the probability of finding a particle in a particular portion of a one-dimensional box, depending on its energy state.

  • How does the probability density function change with the energy state of the particle?

    -The probability density function changes significantly with the energy state of the particle. At the ground state, it resembles a sine or cosine wave, with the highest probability in the middle of the box. However, at the first excited state (second energy level), the probability at the center of the box goes to zero.

  • What is the mathematical equation used to describe the position of a particle in a box?

    -The position of a particle in a box is described by a surging equation, which is modified by the energy level indicator 'n' at the end of the equation.

  • How is the probability density function derived for the ground state?

    -For the ground state (n=1), the probability density function is derived by squaring the function obtained from the surging equation.

  • What is the process to calculate the probability of finding a particle within a specific region in the box?

    -To calculate the probability, one integrates the probability density function from the boundaries X1 to X2 of the region of interest within the box.

  • What is the significance of the integral limits 0.45L and 0.55L?

    -The integral limits 0.45L and 0.55L are chosen to symmetrically straddle the central point of the box, allowing for a more meaningful comparison of probabilities across different energy states.

  • How does the probability of finding a particle in a specific region compare between the ground state and the first excited state?

    -In the ground state, there is a higher probability of finding the particle in the middle of the box, whereas in the first excited state, the probability at the center is zero, indicating a significantly different distribution.

  • What is the final calculated probability of finding the particle between 0.45L and 0.55L?

    -The final calculated probability of finding the particle between 0.45L and 0.55L is 19.8%, despite this range being only 10% of the total distance from 0 to L.

  • What is the implication of the calculated probability for the understanding of particle behavior in a one-dimensional box?

    -The calculated probability enhances our understanding that the behavior and location of a particle in a one-dimensional box are highly dependent on its energy state, with significant variations in the probability density function from one state to another.

  • What will be the focus of the next video?

    -The next video will continue the exploration of particle probability in a one-dimensional box, but this time for the second energy level, to further illustrate how the probability changes with different energy states.

Outlines
00:00
🌟 Introduction to Probability in a One-Dimensional Box

This paragraph introduces the concept of finding the probability of a particle's presence in a specific section of a one-dimensional box, emphasizing how this probability varies with the particle's energy state. It explains that at the ground state, the probability density function resembles a sine or cosine wave, with the highest probability in the middle of the box. In contrast, for the first excited state (N=2), the probability at the box's center is zero. The video aims to calculate the probability for these scenarios, starting with the ground state and using the particle in a box model to derive the probability density function. The process involves squaring the wave function and integrating over the region of interest to find the probability of the particle's presence.

05:04
📈 Calculating Probability for Ground State and First Excited State

This paragraph delves into the mathematical process of calculating the probability of finding a particle in a one-dimensional box for both the ground state and the first excited state. It describes the integration of the probability density function, which is derived from the wave function, over a symmetrical range around the box's center. The calculation involves splitting the integral into two parts and simplifying the expression using trigonometric identities. The result shows that there is a 19.8% chance of finding the particle in a range that represents only 10% of the total length of the box, which is a higher probability than if the particle were distributed evenly. The paragraph concludes by noting that the probability will be significantly different for the second energy level, which will be explored in the next video.

Mindmap
Keywords
💡Probability
In the context of the video, probability refers to the likelihood of finding a particle within a specific region of a one-dimensional box. It is a fundamental concept in quantum mechanics that describes the chance of a particular outcome or event. The video discusses how this probability changes depending on the energy state of the particle, with the ground state and excited states yielding different probability density functions.
💡Particle
A particle, in the context of this video, represents a small, often subatomic, object whose behavior is governed by the principles of quantum mechanics. The video specifically discusses the behavior of a particle within a one-dimensional box, exploring how its probability density function changes with different energy states.
💡One-Dimensional Box
A one-dimensional box, as used in the video, is a theoretical model in quantum mechanics where a particle is confined to move within a straight line between two boundaries. This model is often used to illustrate and understand the concepts of quantization of energy levels and wave-particle duality.
💡Energy State
Energy state refers to the specific value of energy that a quantum system can have. In the video, it is explained that the energy state of a particle in a one-dimensional box affects its probability density function, with ground state and excited states leading to different probabilities of finding the particle in certain regions of the box.
💡Ground State
The ground state is the lowest energy state that a quantum system can occupy. In the context of the video, the ground state is used to describe the lowest energy level of the particle in the one-dimensional box. The probability density function for a particle in the ground state is discussed and compared to that of excited states.
💡Excited State
An excited state is any energy state higher than the ground state. In quantum mechanics, excited states are temporary and unstable configurations of a quantum system. The video discusses how the probability density function for a particle in an excited state differs from that of the ground state, particularly noting that the probability at the center of the box goes to zero.
💡Probability Density Function
The probability density function (PDF) is a mathematical function that describes the relative likelihood for a particle to be found at a certain point within a given region of space. In the context of the video, the PDF is used to illustrate the distribution of probabilities for a particle in different energy states within a one-dimensional box.
💡Quantum Mechanics
Quantum mechanics is a fundamental theory in physics that describes the behavior of matter and energy at very small scales, such as atomic and subatomic particles. The video's discussion of particles in a one-dimensional box, energy states, and probability density functions is rooted in the principles of quantum mechanics.
💡Wave Function
The wave function is a mathematical description of the quantum state of a system. In the context of the video, the wave function is related to the probability density function, which describes the probability of finding a particle in a particular region of space. The wave function's square gives the probability density function.
💡Schrödinger Equation
The Schrödinger Equation is a fundamental equation in quantum mechanics that describes how the quantum state of a physical system changes with time. In the video, the Schrödinger Equation is mentioned as the basis for describing the position of a particle in a box, with the energy level indicated as a subscript.
💡Integration
Integration is a mathematical process that calculates the area under a curve. In the context of the video, integration is used to find the probability of finding a particle within a specific range of the one-dimensional box by integrating the probability density function over that range.
Highlights

Exploration of probability of finding a particle in a specific portion of a one-dimensional box.

The probability depends on the particle's state, specifically its energy level.

At the ground state, the probability density function resembles a sine or cosine wave.

Highest probability at the ground state is found in the middle of the box.

For the first excited state (N=2), the probability density function looks significantly different.

Probability at the center of the box goes to zero for the first excited state.

Calculation of the probability density function for the ground state is demonstrated.

The Schrödinger equation is used to describe the position of a particle in a box.

For the ground state (n=1), squaring the function of the Schrödinger equation yields the probability density function.

Integration of the probability density function over specific boundaries gives the probability of finding the particle.

The integral is split into two parts for simplification, involving the sine and cosine of a specific angle.

The final result shows a 19.8% probability of finding the particle in a 10% section of the box length.

The probability is not evenly distributed across the box, with a higher chance in certain areas.

The video will continue to explore the probability for particles in higher energy states in future content.

The particle's probability distribution in a one-dimensional box varies greatly with its energy state.

The practical application of these findings can help understand quantum behavior in particles.

The method used can be applied to find probabilities in three-dimensional boxes as well.

The video provides a clear and detailed explanation of the mathematical process involved in finding these probabilities.

Transcripts

Browse More Related Video

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (27 of 92) Expectation Value=? 1-D Box n=1

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (18 of 92) Particle in 1-D Box: Gen. Appr.

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (20 of 92) Particle in 1-D Box: Example 2/2

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (10 of 92) What is Normalization? Ex. 1

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (19 of 92) Particle in 1-D Box: Example 1/2

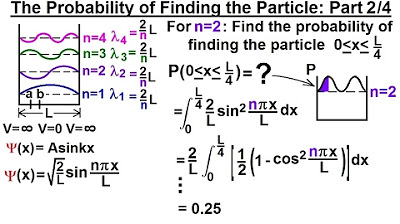
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (22 of 92) Prob. of Finding Particle 2

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
QuantumMechanicsProbabilityCalculationsParticleStatesOneDimensionalBoxGroundStateExcitedStatesWaveFunctionsSchrodingerEquationPhysicsEducationMathematicalAnalysis